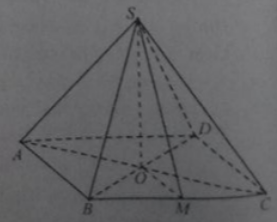
Cho hình chóp tam giác đều S.ABC với SA = 2AB. Góc giữa (SAB) và (ABC) bằng a. Chọn khẳng định đúng trong các khẳng định sau?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi O là tâm của tam giác đều ABC
Gọi \(CO \cap AB = H\) suy ra H là trung điểm AB(\(\Delta ABC\) vì đều)
\( \Rightarrow OH \bot AB\) và \(OH = \frac{1}{3}CH = \frac{1}{3}.\frac{{AB\sqrt 3 }}{2} = \frac{{AB\sqrt 3 }}{6}\)
Tìm góc giữa (SAB) và (ABC)
\(\left\{ {\begin{array}{*{20}{c}} {\left( {SAB} \right) \cap \left( {ABC} \right) = AB}\\ {OH \bot AB}\\ {SO \bot AB{\rm{ }}\left( {SO \bot (ABC)} \right){\rm{ }}} \end{array}} \right.\)
\(\Rightarrow SH \bot AB\) (1)
Ta có
\(\left\{ {\begin{array}{*{20}{c}} {\left( {SAB} \right) \cap \left( {ABC} \right) = AB}\\ {OH \bot AB,{\rm{ }}OH \subset (ABC)}\\ {SH \bot AB,SH \subset (SAB){\rm{ }}} \end{array}} \right.\)
\( \Rightarrow \left( {\widehat {(SAB);(ABC)}} \right) = \left( {\widehat {SH;OH}} \right) = \widehat {SHO} = \alpha \)
Từ (1) suy ra \(SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{{\left( {2AB} \right)}^2} - {{\left( {\frac{{AB}}{2}} \right)}^2}} = \frac{{\sqrt {15} }}{2}AB\)
Từ đó ta có : \(\cos \alpha = \frac{{OH}}{{SH}} = \frac{{\frac{{\sqrt 3 }}{6}AB}}{{\frac{{\sqrt {15} }}{2}AB}} = \frac{1}{{3\sqrt 5 }}\)
Câu hỏi liên quan
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\), gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(S A \perp(A B C D)\), gọi O là tâm hình vuông ABCD . Khẳng định nào sau đây sai?
-
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Mặt phẳng (ABD) vuông góc với mặt phẳng nào của tứ diện?
-
Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc. Đường thẳng DE vuông góc?
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Gọi M là trung điểm của SB. Góc giữa AM và BD bằng
-
Cho tứ diện đều ABCD. Góc giữa (ABC) và (ABD) bằng \(\alpha\). Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tâm của đáy là O. Gọi M và N lần lượt là trung điểm của SA và BC. Biết rằng góc giữa MN và (ABCD) bằng 60o, cosin góc giữa MN và mặt phẳng (SBD) bằng :
-
Trong các mệnh đề sau, mệnh đề nào sai?
-
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC') có số đo bằng 60o. Cạnh bên của hình lăng trụ bằng:
-
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính của góc giữa một mặt bên và một mặt đáy.
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa mặt bên hình chóp S.ABCD và mặt phẳng đáy có tang bằng:
-
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60o. Gọi M và N lần lượt là trung điểm của AB và CD.
Góc giữa hai mặt phẳng (ACD) và (BCD) là:
-
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có ACC'A' là hình vuông, cạnh bằng a. Cạnh đáy của hình lăng trụ bằng:
-
Mệnh đề nào sau đây là đúng?
-
Tính cosin của góc giữa hai mặt của một tứ diện đều.
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có \(S A=S B=S C=a\) . Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng?
-
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a . Tính cosin của góc giữa một mặt bên và một mặt đáy
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Cắt hình lập phương bởi mặt phẳng trung trực của AC'. Thiết diện là hình gì?
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
.png)
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có tâm O và \(SA \bot \left( {ABCD} \right)\). Khẳng định nào sau đây sai ?
