Trắc nghiệm Hai mặt phẳng vuông góc Toán Lớp 11
-
Câu 1:
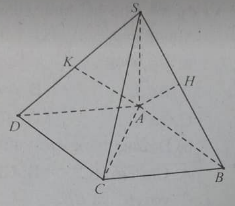
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAC) và (AHK) vuông góc vì:
.png)
A. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD)
B. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD) nên SC⊥(AHK)
C. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC) nên SC⊥(AHK)
D. AK ⊥(SBC) (do AK ⊥ SD và AK ⊥ CD) nên SC ⊥ (AHK)
-
Câu 2:
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAB) và (SBC) vuông góc vì.
A. Góc của (SAB) và (SBC) là góc ABC và bằng 90o
B. Góc của (SAB) và (SBC) là góc BAD và bằng 90o
C. AB ⊥ BC; AB ⊂ (SAB) và BC ⊂ (SBC)
D. BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA














