Trắc nghiệm Số phức Toán Lớp 12
-
Câu 1:
Gọi A là điểm biểu diễn của số phức z = 4 -7i và B là điểm biểu diễn của số phức z ' = -4+7i. Mệnh đề nào sau đây là đúng?
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng nhau qua trục tung.
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O.
D. Hai điểm A và B đối xứng nhau qua đường thẳng y = x
-
Câu 2:
Gọi A là điểm biểu diễn của số phứcz=2+5iz=2+5i và B là điểm biểu diễn của số phức z′=−2+5iz′=−2+5i . Mệnh đề nào sau đây là đúng?
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng nhau qua trục tung.
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O .
D. Hai điểm A và B đối xứng nhau qua đường thẳng y = x.
-
Câu 3:
Gọi A là điểm biểu diễn của số phức z=−1+6iz=−1+6ivà B là điểm biểu diễn của số phức z′=−1−6iz′=−1−6i. Mệnh đề nào sau đây là đúng?
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng nhau qua trục tung.
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O .
D. Hai điểm A và B đối xứng nhau qua đường thẳng y=x.
-
Câu 4:
Trong mặt phẳng tọa độ cho hai điểm A(4;0) và B(0;-3). Điểm C thỏa mãn điều kiện →OC=→OA+→OB−−→OC=−−→OA+−−→OB . Khi đó, số phức được biểu diễn bởi điểm C là:
A. z=−3−4iz=−3−4i
B. z=4−3iz=4−3i
C. z=−3+4iz=−3+4i
D. z=4+3iz=4+3i
-
Câu 5:
Trong mặt phẳng tọa độ, điểm M là điểm biểu diễn của số phức z (như hình vẽ bên). Điểm nào trong hình vẽ là điểm biểu diễn của số phức 2z ?
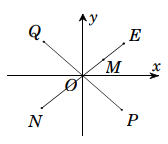
A. Điểm N
B. Điểm Q
C. Điểm E
D. Điểm P
-
Câu 6:
Giả sử M, N, P, Q, đượccho ở hình vẽ bên là điểm biểu diễn của các số phức z1,z2,z3,z4z1,z2,z3,z4 trênmặt phẳng tọa độ. Khẳng định nào sau đây là đúng?
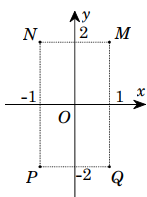
A. Điểm M là điểm biểu diễn số phức z1=2+iz1=2+i
B. Điểm Q là điểm biểu diễn số phức z4=−1+2iz4=−1+2i
C. Điểm N là điểm biểu diễn số phức z2=2−iz2=2−i
D. Điểm P là điểm biểu diễn số phức z3=−1−2iz3=−1−2i
-
Câu 7:
Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình vẽ?
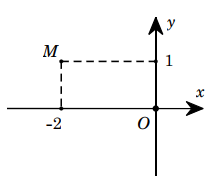
A. z4=2+i
B. z2=1+2i
C. z3=−2+i
D. z1=1−2i
-
Câu 8:
Trong mặt phẳng tọa độ (hình vẽbên), số phức z=3-4i được biểu diễn bởi điểm nào trong các điểm A, B, C, D?
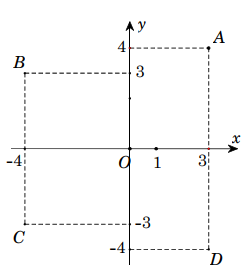
A. Điểm A
B. Điểm B
C. Điểm C
D. Điểm D
-
Câu 9:
Cho số phức z=1−2i . Điểm nào dưới đây là điểm biểu diễn của số phức w=iz trên mặt phẳng tọa độ?
A. Q(1;2)
B. N(2;1)
C. M(1;-2)
D. P(-2;1)
-
Câu 10:
Điểm biểu diễn số phức z=2-3i có tọa độ là:
A. (2;3)
B. (-2;-3)
C. (2;-3)
D. (-2;3)
-
Câu 11:
Với x y , là hai số thực thỏa mãn x(3+5i)+y(1−2i)3=9+14i . Tính giá trị của biểu thức P=2x−3y
A. P=205109
B. P=35361
C. P=17261
D. P=94109
-
Câu 12:
Cho số phức z=x+iy thỏa mãn z2=−8+6i . Mệnh đề nào sau đây là sai?
A. {x2−y2=−8xy=3
B. {x4+8x2−9=0y=3x
C. {x=1y=3 hoặc {x=−1y=−3
D. x2+y2+2xy=−8+6i
-
Câu 13:
Cho hai số phức z1=a+bi(a;b∈R) và z2=3−4i. Biết z1=z22, tính P=ab
A. 168
B. -600
C. 31
D. -12
-
Câu 14:
Tìm tất cả các số thực x, y thỏa mãn x2+y−(2y+4)i=2i
A. (x;y)=(√3;−3) hoặc (x;y)=(−√3;3)
B. (x;y)=(√3;3) hoặc (x;y)=(√3;−3)
C. (x;y)=(√3;−3) hoặc (x;y)=(−√3;−3)
D. (x;y)=(√3;3) hoăc (x;y)=(−√3;−3)
-
Câu 15:
Tìm tất cả các số thực x; y sao cho x2−1+yi=−1+2i.
A. x=0;y=2
B. x=√2;y=−2
C. x=√2;y=2
D. x=−√2;y=2
-
Câu 16:
Cho hai số thực x y , thỏa mãn 2x+3+(1−2y)i=2(2−i)−3yi+x. Tính giá trị biểu thức P=x2−3xy−y.
A. 13
B. -3
C. 11
D. -12
-
Câu 17:
Tìm tất cả các số thực x y ; thỏa mãn (2x−y)i+y(1−2i)2=3+7i
A. x=1;y=−1
B. x=1;y=1
C. x=−1;y=1
D. x=−1;y=−1
-
Câu 18:
Biết rằng có duy nhất một cặp số thực (x;y) thỏa mãn (x+y)+(x−y)i=5+3i. Tính S=x+y
A. 5
B. 3
C. 4
D. 6
-
Câu 19:
Cho hai số phức z=(2x+3)+(3y−1)i và z′=3x+(y+1)i. Khi z=z′ , chọn khẳng định đúng trong các khẳng định sau:
A. x=−53;y=0
B. x=−53;y=43
C. x=3;y=1
D. x=1;y=3
-
Câu 20:
Cho hai số phức z1=a+bi(a;b∈R) và z2=2017−2018i . Biết z1=z2 tính tổng S=a+2b
A. -1
B. 4035
C. -45
D. -2019
-
Câu 21:
Tập hợp các điểm trong mặt phẳng toạ độ biểu diễn các số phức z thoả mãn |z+4−8i|=2√5 là đường tròn có phương trình:
A. (x+4)2+(y−8)2=20
B. (x+4)2+(y−8)2=2√5
C. (x−4)2+(y+8)2=2√5
D. (x−4)2+(y+8)2=20
-
Câu 22:
Tập hợp các điểm biểu diễn cho số phức z thỏa mãn |z−3+4i|=5 là
A. Một đường Elip
B. Một đường tròn.
C. Một đường thẳng
D. Một đường parabol.
-
Câu 23:
Trong mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn |z−i|=|(1+i)z|là một đường tròn, đường tròn đó có phương trình là
A. x2+y2+2x+2y−1=0
B. x2+y2+2x+1=0
C. x2+y2+2x−1=0
D. x2+y2+2y−1=0
-
Câu 24:
Trên mặt phẳng phức, tập hợp các điểm biểu diễn số phức z thỏa mãn |z+i|=|2¯z−i|là một đường tròn có bán kính là R . Tính giá trị của R.
A. R=1
B. R=19
C. R=23
D. R=13
-
Câu 25:
Tập hợp điểm biểu diễn các số phức thỏa |zi+1|=11 là một đường tròn. Tìm tâm I của đường tròn đó
A. I(0;-1)
B. I(0;1)
C. I(-1;0)
D. I(1;0)
-
Câu 26:
Tập hợp điểm biểu diễn các số phức z thỏa mãn |z−i|=|¯z+3|trong mặt phẳng Oxy là:
A. Đường thẳng Δ:3x−y+4=0
B. Đưởng thẳng Δ:x+y+4=0
C. Đường thẳng Δ:3x+y+4=0
D. Đường thẳng Δ:x+y−4=0
-
Câu 27:
Trong mặt phẳng phức, tập hợp các điểm biểu diễn của số phức z thỏa mãn điều
kiện |z+2|=|i−z| là đường thẳng Δ có phương trìnhA. 4x−2y+3=0
B. 4x+2y+3=0
C. 2x+4y+13=0
D. −2x+4y−13=0
-
Câu 28:
Tìm tập hợp điểm biểu diễn của số phức z biết |z−1|=|z+2i|
A. Hypebol.
B. Đường tròn.
C. Đường thẳng.
D. Parabol.
-
Câu 29:
Trong mặt phẳng phức với hệ tọa độ Oxy , điểm biểu diễn của các số phức z=3+bivớib∈R luôn nằm trên đường có phương trình là:
A. y=3
B. y=x+3
C. x=3
D. y=x
-
Câu 30:
Tập hợp điểm biểu diễn số phức z thỏa mãn |z|2=z2 là
A. Một đường tròn
B. Một điểm .
C. Một đường thẳng.
D. Một đoạn thẳng
-
Câu 31:
Tìm tập hợp những điểm M biểu diễn số phức z trong mặt phẳng phức, biết số phức z thỏa mãn điều kiện |z−2i|=|¯z+1|
A. Tập hợp những điểm M là đường thẳng có phương trình 4x + 2 y + 3 = 0 .
B. Tập hợp những điểm M là đường thẳng có phương trình 4x - 2 y + 3 = 0 .
C. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4 y + 3 = 0 .
D. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4 y - 3 = 0 .
-
Câu 32:
Cho các số phức z thỏa mãn |z+1−i|=|z−1+2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. 4x−6y−3=0
B. 4x+6y+3=0
C. 4x+6y−3=0
D. 4x−6y+3=0
-
Câu 33:
Trong mặt phẳng phức tập hợp điểm M ( z ) thoả mãn z0z+¯z0z+1=0vớiz0=1−i là đường thẳng có phương trình
A. 2x+2y=1=0
B. -2x+2y-1=0
C. -2x-2y-1=0
D. 2x-2y-1=0
-
Câu 34:
Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z2=(¯z)2 là:
A. Trục hoành
B. Trục tung
C. Gồm cả trục hoành và trục tung
D. Đường thẳng y=x
-
Câu 35:
Cho các số phức z1=−1+i,z2=2+3i,z3=5+i,z4=2−i lần lượt có các điểm biểu diễn trên mặt phẳng phức là M, N, P,Q . Hỏi tứ giác MNPQ là hình gì?
A. Tứ giác MNPQ là hình thoi
B. Tứ giác MNPQ là hình vuông
C. Tứ giác MNPQ là hình bình hành
D. Tứ giác MNPQ là hình chữ nhật
-
Câu 36:
Cho số phức z=m+(m−3)i,m∈R . Tìm m để điểm biểu diễn của số phức z nằm trên đường phân giác của góc phần tư thứ hai và thứ tư.
A. m=0
B. m=23
C. m=12
D. m=32
-
Câu 37:
Gọi M là điểm biểu diễn số phức z=i(1+2i)2 . Tọa độ của điểm M là
A. M(4;-3)
B. M(4;3)
C. M(-4;3)
D. M(-4;-3)
-
Câu 38:
Cho số phức z=(1+2i)(2−i), điểm biểu diễn của số phức i.z là
A. M(4;3)
B. M(-3;4)
C. M(3;4)
D. M(4;-3)
-
Câu 39:
Cho số phức z = 1 + 2i . Điểm nào dưới đây là điểm biểu diễn của số phức w=z+i¯z trên mặt phẳng toạ độ?
A. P(-3;3)
B. M(3;3)
C. Q(3;2)
D. N(2;3)
-
Câu 40:
Giả sử A, B theo thứ tự là điểm biểu diễn của số phức z1,z2 . Khi đó độ dài của AB bằng
A. |z1|−|z2|
B. |z1+z2|
C. |z1−z2|
D. |z1|+|z2|
-
Câu 41:
Gọi A , B lần lượt là các điểm biểu diễn của các số phức z1=1+2i;z2=5−i. Tính độ dài đoạn thẳng AB
A. √5+√26
B. 5
C. 25
D. √37
-
Câu 42:
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z tìm phần thực và phần ảo của số phức z
.png)
A. Phần thực là 1 và phần ảo là -2i
B. Phần thực là 2 và phần ảo là -1
C. Phần thực là -2 và phần ảo là i
D. Phần thực là 1 và phần ảo là -2
-
Câu 43:
Cho số phức z = 5 - 4i . Số phức đối của z có điểm biểu diễn là
A. (-5;4)
B. (-5;-4)
C. (5;4)
D. (5;-4)
-
Câu 44:
Điểm A trong hình vẽ bên biểu diễn cho số phức z
.png)
Tìm phần thực và phần ảo của số phức ¯z
A. Phần thực là -3 và phần ảo là 2i
B. Phần thực là -3 và phần ảo là 2
C. Phần thực là 3 và phần ảo là -2i
D. Phần thực là 3 và phần ảo là -2
-
Câu 45:
Cho số phức z thoả mãn (2+i)z=10−5i . Hỏi điểm biểu diễn số phức z là điểm nào trong các điểm M,N, P, Q ở hình bên ?
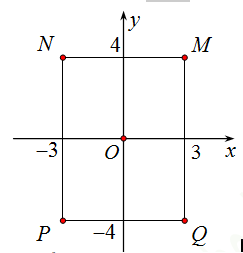
A. Điểm N
B. Điểm M
C. Điểm P
D. Điểm Q
-
Câu 46:
Điểm M trong hình vẽ bên biểu diễn số phức ¯z.
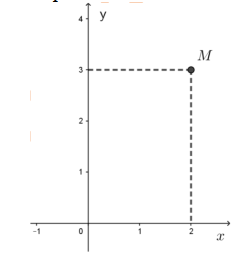
Số phức z bằng
A. 3+2i
B. 3-2i
C. 2+3i
D. 2-3i
-
Câu 47:
Trong hình vẽ bên, điểm M biểu diễn số phức z . Số phức ¯z
.png)
A. 2+i
B. 2-i
C. 1+2i
D. 1-2i
-
Câu 48:
Mệnh đề nào dưới đây sai?
A. Điểm M (-1; 2) là điểm biểu diễn số phức z = -1+ 2i
B. Số phức z=√2i là số thuần ảo.
C. Mô đun của số phức z=a+bi(a,b∈R)là a² + b²
D. Số phức z = 5 - 3i có phần thực là 5 , phần ảo -3
-
Câu 49:
Phần thực của số phức (1+i)30 bằng
A. 0
B. 215
C. −215
D. 1
-
Câu 50:
Tìm phần ảo của số phức z=(1−i)2+(1+i)2 .
A. -4
B. 0
C. 2
D. 4














