Trắc nghiệm Số phức Toán Lớp 12
-
Câu 1:
Điểm M trong hình vẽ dưới đây biểu diễn số phức .
.png)
Số phức z bằng ?
A. 2 -3i
B. 2+3i
C. 3+2i
D. 3-2i
-
Câu 2:
Cho số phức z thỏa mãn điều kiện . Điểm M là điểm biểu diễn số phức z trên mặt phẳng tọa độ Oxy. Tọa độ của điểm M là
A.
B.
C.
D.
-
Câu 3:
Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức ?
.png)
A. P
B. M
C. N
D. Q
-
Câu 4:
Cho số phức z = 1 + 2i . Điểm nào dưới đây là điểm biểu diễn của số phức trên mặt phẳng toạ độ?
A. M(3;3)
B. Q(3;2)
C. P(2;3)
D. N(-3;3)
-
Câu 5:
Cho số phức z = 2018 - 2017i. Điểm M biểu diễn của số phức liên hợp của là
A. M(-2018;2017)
B. M(2018;-2017)
C. M(2018;2017)
D. M(-2018; -2017)
-
Câu 6:
Biểu diễn hình học của số phức z = 2 -3i là điểm nào trong những điểm sau đây?
A. I(-2;3)
B. I(2;-3)
C. I(2;3)
D. I(-2;-3)
-
Câu 7:
Tìm tọa độ điểm M là điểm biểu diễn số phức z biết z thỏa mãn phương trình .
A. M(-1;4)
B. M(1;4)
C. M(-1;-4)
D. M(1;-4)
-
Câu 8:
Cho số phức z = -4+5i . Biểu diễn hình học của z là điểm có tọa độ
A. (-4;5)
B. (-4;-5)
C. (4;-5)
D. (4;5)
-
Câu 9:
Số phức liên hợp của số phức z = i(1-2i) có điểm biểu diễn là điểm nào dưới đây?
A. E(2;-1)
B. B(-1;2)
C. A(1;2)
D. F(-2;1)
-
Câu 10:
Hỏi điểm M(3;-1) là điểm biểu diễn số phức nào sau đây?
A. z = -1 + 3i
B. z = 1 - 3i
C. z = 3 - i
D. z = -3 + i
-
Câu 11:
Cho số phức , thỏa mãn
A. -5
B. 5
C. -3
D. 3
-
Câu 12:
Tính môđun của số phức z thỏa mãn
A. 2
B. 4
C.
D.
-
Câu 13:
Cho số phức z thỏa điều kiện . Tính môđun của số phức
A.
B.
C.
D.
-
Câu 14:
Cho số phức z thỏa mãn . Tìm phần ảo của số phức
A.
B.
C.
D.
-
Câu 15:
Cho số phức . Khi đó môđun của z bằng
A. 1
B.
C. 13
D.
-
Câu 16:
Tìm các số thực x, y thỏa mãn .
A.
B.
C.
D.
-
Câu 17:
Cho số phức z thỏa mãn . Xác định phần thực, phần ảo của số phức.
A. Phần thực là -2; phần ảo là 5 .i
B. Phần thực là -2; phần ảo là 5
C. Phần thực là -2; phần ảo là 3.
D. Phần thực là -3; phần ảo là 5 .
-
Câu 18:
Cho số phức z thỏa . Mô đun của số phức z là:
A.
B.
C.
D.
-
Câu 19:
Cho z, w là các số phức thỏa mãn . Tìm tập hợp các điểm biểu diễn của số phức w .
A. Hình tròn .
B. Đường tròn
C. Hình tròn
D. Đường tròn
-
Câu 20:
Xét các số phức có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình . Tìm tập hợp các điểm biểu diễn của số phức
A. Đường thẳng.
B. Đoạn thẳng
C. Điểm.
D. Đường tròn
-
Câu 21:
Số phức z thỏa mãn điều kiện nào sau đây thì có tập hợp các điểm biểu diễn của nó trên mặt phẳng tọa độ là đường tròn tâm I (0;1), bán kính R =2?
A.
B.
C.
D.
-
Câu 22:
Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện là số thuần ảo là:
A. Đường tròn có tâm
B. Đường thẳng nối hai điểm A(2;0) và B(0;1)
C. Đường tròn có tâm nhưng bỏ đi hia điểm
D. Đường trung trực của đoạn thẳng AB với A(2;0) và B(0;1)
-
Câu 23:
Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện là:
A. Đường tròn có tâm I (-3;0) , bán kính R = 3
B. Đường tròn có tâm I (3;0) , bán kính R = 3
C. Đường tròn có tâm I (-3;0) , bán kính R = 9
D. Đường tròn có tâm I (3;0) , bán kính R = 9
-
Câu 24:
Trong mặt phẳng tọa độ, tập hợp các điểm M(x;y) biểu diễn của số phức thỏa mãn là số thực là:
A. Đường tròn nhưng bỏ hai điểm (0;1) và (0;-1)
B. Parabol
C. Trục hoành.
D. Trục tung bỏ điểm biểu diễn số phức z= i
-
Câu 25:
Trong mặt phẳng tọa độ, tập hợp các điểm M(x;y)biểu diễn của số phức thỏa mãn là:
A. Đường tròn tâm O bán kính R=1
B. Đường tròn đường kính AB với
C. Đường trung trực của đoạn thẳng AB với
D. Đường thẳng vuông góc với đoạn AB tại A với
-
Câu 26:
Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện là
A. Trục hoành.
B. Trục hoành và trục tung.
C. Đường phân giác góc phần tư thứ nhất và thứ ba
D. Các đường phân giác của các gốc tọa độ
-
Câu 27:
Trong mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z có phần thực bằng 2 là đường thẳng có phương trình:
A. x=-2
B. x=2
C. x=1
D. x=-1
-
Câu 28:
Cho các số phức , thỏa mãn . Gọi M, N lần lượt là điểm biểu diễn các số phức , sao cho với O là gốc tọa độ. Tính giá trị biểu thức
A.
B.
C. P=5
D. P=4
-
Câu 29:
Tìm môđun của số phức z biết
A.
B.
C.
D.
-
Câu 30:
Xét số phức z thỏa mãn . Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
-
Câu 31:
Xét số phức z thỏa mãn Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
-
Câu 32:
Cho số phức . Mệnh đề nào sau đây là đúng?
A.
B.
C.
D.
-
Câu 33:
Cho là hai số phức thỏa mãn và . Tính giá trị của biểu thức
A. P=1008
B.
C. P=36
D.
-
Câu 34:
Cho là hai số phức thỏa mãn biết . Tính giá trị biểu thức
A.
B.
C.
D.
-
Câu 35:
Cho hai số phức , thỏa mãn
A.
B.
C.
D.
-
Câu 36:
Tính tổng các phần thực của các số phức z thỏa mãn có phần ảo bằng 1.
A. 2
B. 1
C. 3
D. 0
-
Câu 37:
Cho số phức z thỏa mãn . Tính tổng phần thực và phần ảo của z
A. 0
B. 1
C. -1
D. 2
-
Câu 38:
Có bao nhiêu số phức z thỏa mãn và là số thực.
A. 0
B. 1
C. 2
D. 3
-
Câu 39:
Có bao nhiêu số phức z thỏa mãn là số thuần ảo.
A. 0
B. 4
C. 3
D. 2
-
Câu 40:
Cho số phức z thỏa mãn . Tính
A.
B.
C.
D.
-
Câu 41:
Cho số phức . Tính
A.
B. -5
C. 5
D.
-
Câu 42:
Cho số phức z thỏa mãn . Tính
A. 144
B.
C. 12
D. 0
-
Câu 43:
Tính môđun của số phức z , biết z thỏa mãn
A. 4
B. 2
C.
D. 10
-
Câu 44:
Gọi M là điểm biểu diễn của số phức z , biết tập hợp các điểm M là phần tô đậm ở hình bên (kể cả biên). Mệnh đề nào sau đây đúng ?
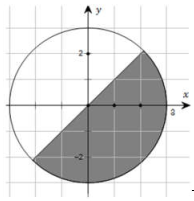
A. z có phần ảo không nhỏ hơn phần thực.
B. z có phần thực không nhỏ hơn phần ảo và có môđun không lớn hơn 3.
C. z có phần thực bằng phần ảo.
D. z có môđun lớn hơn 3.
-
Câu 45:
Một hình vuông tâm là gốc tọa độ O , các cạnh song song với các trục tọa độ và có độ dài bằng 4 . Hãy xác định điều kiện của a và b để điểm biểu diễn số phức z=a+bi nằm trên đường chéo của hình vuông.
A.
B.
C.
D.
-
Câu 46:
Gọi M là điểm biểu diễn của số phức z , biết tập hợp các điểm M là phần tô đậm ở hình bên (kể cả biên). Mệnh đề nào sau đây đúng ?
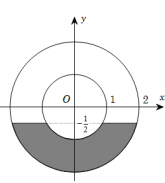
A. và phần ảo lớn hơn
B. và phần ảo lớn hơn
C.
D. và phần ảo nhỏ hơn
-
Câu 47:
Gọi M là điểm biểu diễn của số phức z , biết tập hợp các điểm M là phần tô đậm ở hình bên (không kể biên). Mệnh đề nào sau đây đúng :
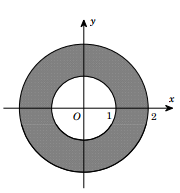
A.
B.
C.
D.
-
Câu 48:
Trong mặt phẳng tọa độ, cho số phức với . Khi đó điểm biểu diễn số phức z nằm trên trên đường có phương trình nào trong các phương trình sau?
A. Parabol
B. Parabol
C. Đương thẵng y=2 x
D. Parabol
-
Câu 49:
Trong mặt phẳng tọa độ, điểm biểu diễn của các số phức với luôn nằm trên đường có phương trình nào trong các phương trình sau?
A.
B.
C.
D.
-
Câu 50:
Gọi A là điểm biểu diễn của số phức và B là điểm biểu diễn của số phức . Mệnh đề nào sau đây là đúng?
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng nhau qua trục tung.
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O .
D. Hai điểm A và B đối xứng nhau qua đường thẳng y = x














