Trắc nghiệm Hàm số lượng giác Toán Lớp 11

Câu 1:

Tìm chu kì của các hàm số sau $y = \tan x + \tan \frac{x}{2}$

A. $T_0=3\pi$

B. $T_0=2\pi$

C. $T_0=\pi$

D. $T_0=4\pi$
Câu 2:

Tìm chu kì của các hàm số sau y = tan x.tan 3x

A. $T_0=3\pi$

B. $T_0=2π$

C. $T_0=\pi/3$

D. $T_0=\pi$
Câu 3:

Tìm giá trị nhỏ nhất của hàm số $y = tan ^2x - 4tan x + 1$

A. miny=−2

B. miny=−3

C. miny=−4

D. miny=−1
Câu 4:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = 2sin ^2x + cos ^22x$

A. $\max y = 4;\min y = \frac{3}{4}$

B. $maxy=3;miny=2$

C. $maxy=4;miny=2$

D. $\max y = 3;\min y = \frac{3}{4}$
Câu 5:

Tìm chu kì cơ sở (nếu có) của các hàm số sau $y = sin 3x + 2cos 2x$

A. $T _0 = 2 π$

B. $T _0 = π$

C. $T _0 = 3 π$

D. $T _0 = 4 π$
Câu 6:

Tìm tập xác định của hàm số $y = \sqrt {\frac{{1 - \cos 3x}}{{1 + \sin 4x}}}$

A. $D = R \setminus \left\{ { - \frac{\pi }{8} + k\frac{\pi }{4},k \in Z} \right\}$

B. $D = R \setminus \left\{ { - \frac{3\pi }{8} + k\frac{\pi }{2},k \in Z} \right\}$

C. $D = R \setminus \left\{ { - \frac{\pi }{8} + k\frac{\pi }{2},k \in Z} \right\}$

D. $D = R \setminus \left\{ { k\frac{2\pi }{3},k \in Z} \right\}$
Câu 7:

Tìm chu kì của các hàm số sau $f( x ) = sin 2x + sin x$

A. $T_0=2π$

B. $T_0=3π$

C. $T_0=π$

D. $T_0=4\pi$
Câu 8:

Tìm tập xác định của hàm số sau $y= \tan \left( {2x + \frac{\pi }{3}} \right)$

A. $D = R \setminus \left\{ {\frac{\pi }{3} + k\frac{\pi }{2};k \in Z} \right\}$

B. $D = R \setminus \left\{ {\frac{\pi }{4} + k\frac{\pi }{2};k \in Z} \right\}$

C. $D = R \setminus \left\{ {\frac{\pi }{12} + k\frac{\pi }{2};k \in Z} \right\}$

D. $D = R \setminus \left\{ {\frac{\pi }{8} + k\frac{\pi }{2};k \in Z} \right\}$
Câu 9:

Tìm tập xác định của hàm số $y= \tan \left( {2x - \frac{\pi }{4}} \right)$

A. $D = R \setminus \left\{ {\frac{\pi }{8} + \frac{{k\pi }}{2},k \in Z} \right\}$

B. $D = R \setminus \left\{ {\frac{3\pi }{8} + \frac{{k\pi }}{2},k \in Z} \right\}$

C. $D = R \setminus \left\{ {\frac{3\pi }{8} + {k\pi },k \in Z} \right\}$

D. $D = R \setminus \left\{ {\frac{3\pi }{4} + \frac{{k\pi }}{2},k \in Z} \right\}$
Câu 10:

Tìm tập xác định của hàm số sau $y = tan 3x.cot 5x$

A. $D = R \setminus \left\{ {\frac{\pi }{4} + k\frac{\pi }{3},\frac{{n\pi }}{5};k,n \in Z} \right\}$

B. $D = R \setminus \left\{ {\frac{\pi }{5} + k\frac{\pi }{3},\frac{{n\pi }}{5};k,n \in Z} \right\}$

C. $D = R \setminus \left\{ {\frac{\pi }{6} + k\frac{\pi }{4},\frac{{n\pi }}{5};k,n \in Z} \right\}$

D. $D = R \setminus \left\{ {\frac{\pi }{6} + k\frac{\pi }{3},\frac{{n\pi }}{5};k,n \in Z} \right\}$
Câu 11:

Hàm số $y = \frac{{1 - 2\sin x}}{{\cos 3x - 1}}$ xác định trên:

A. $D = R \setminus \left\{ {\frac{{k2\pi }}{3},k \in Z} \right\}$

B. $% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbb % a9q8WqFfeaY-biLkVcLq-JHqpepeea0-as0Fb9pgeaYRXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % Gaamiraiabg2da9mrr1ngBPrwtHrhAYaqeguuDJXwAKbstHrhAGq1D % VbacfaGae8xhHi1efv3ySLgznfgDOfdarCqr1ngBPrginfgDObYtUv % gaiyaacqGFwiIGdaGadaWdaeaapeWaaSaaa8aabaWdbiabec8aWbWd % aeaapeGaaGOnaaaacqGHRaWkdaWcaaWdaeaapeGaam4Aaiabec8aWb % WdaeaapeGaaG4maaaacaGGSaGaam4AaiabgIGiolab-rsiAbGaay5E % aiaaw2haaaaa!5B56! D = R\setminus \left\{ {\frac{\pi }{6} + \frac{{k\pi }}{3},k \in Z} \right\}$

C. $D = R \setminus \left\{ {\frac{{k\pi }}{3},k \in Z} \right\}$

D. $D = R \setminus \left\{ {\frac{{k\pi }}{2},k \in Z} \right\}$
Câu 12:

Tìm chu kì của các hàm số sau $f\left( x \right) = \sin \left( {x + \frac{\pi }{5}} \right)$

A. $T_0=2π$

B. $T_0=π$

C. $T_0=3π$

D. $T_0=4π$
Câu 13:

Tìm chu kì của hàm số y = f( x ) = tan 2x

A. ${T_0} = 2\pi$

B. ${T_0} = \frac{\pi }{2}$

C. ${T_0} = \pi$

D. ${T_0} = 4\pi$
Câu 14:

Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số $\frac{3}{{1 + \sqrt {2 + {{\sin }^2}x} }}$

A. $\min y = \frac{{ - 3}}{{1 + \sqrt 3 }};\max y = \frac{3}{{1 + \sqrt 2 }}$

B. $\min y = \frac{3}{{1 + \sqrt 3 }};\max y = \frac{4}{{1 + \sqrt 2 }}$

C. $\min y = \frac{2}{{1 + \sqrt 3 }};\max y = \frac{3}{{1 + \sqrt 2 }}$

D. $\min y = \frac{3}{{1 + \sqrt 3 }};\max y = \frac{3}{{1 + \sqrt 2 }}$
Câu 15:

Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số ${\frac{4}{{1 + 2{{\sin }^2}x}}}$

A. $\min y = \frac{4}{3};\max y = 4$

B. $\min y = \frac{4}{3};\max y = 3$

C. $\min y = \frac{4}{3};\max y = 2$

D. $\min y = \frac{4}{3};\max y = 1$
Câu 16:

Đồ thị hàm số y = tan x nhận đường thẳng nào sau đây là tiệm cận?

A. $y = \frac{\pi }{3} + k\pi \left( {k \in Z} \right)$

B. $x=kπ(k∈Z)$

C. $x = \frac{\pi }{2} + k\pi \left( {k \in Z} \right)$

D. $y = \frac{{k\pi }}{2}\left( {k \in Z} \right)$
Câu 17:

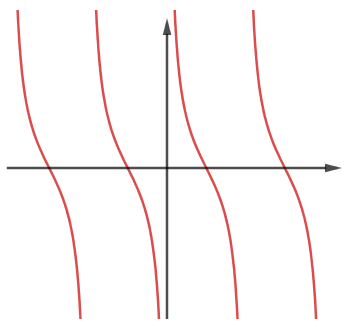
Đường cong trong hình có thể là đồ thị của hàm số nào dưới đây?

A. y=cot⁡x

B. y=tan⁡x

C. y=sin⁡x

D. y=cosx
Câu 18:

Chọn mệnh đề đúng:

A. Hàm số y=sin⁡x có chu kỳ T=π

B. Hàm số y=cos⁡x và hàm số y=tan⁡x có cùng chu kỳ

C. Hàm số y=cot⁡x và hàm số y=tan⁡x có cùng chu kỳ.

D. Hàm số y=cot⁡x có chu kỳ T=2π
Câu 19:

Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y = 3 - 2cos ^2 3x$

A. miny=1;maxy=2

B. miny=1;maxy=3

C. miny=2;maxy=3

D. miny=−1;maxy=3
Câu 20:

Tìm tập giá trị nhỏ nhất, giá trị lớn nhất của hàm số sau $y = 1 + 3\sin \left( {2x - \frac{\pi }{4}} \right)$

A. maxy=−2,miny=4

B. maxy=2,miny=4

C. maxy=−2,miny=3

D. maxy=4,miny=−2
Câu 21:

Trong các hàm số sau đây là hàm số lẻ

A. $y = \sin x.{\cos ^2}x + \tan x$

B. $y = \frac{{{\rm{cos}}2x}}{{{x^2}}}$

C. $y = \left| {\sin x - x} \right|$

D. $y = {\cot ^2}x.$
Câu 22:

Hàm số nào dưới đây là hàm số chẵn?

A. $y = {x^2} - \sin x$

B. $y = {x^2} + \sin x$

C. $y = {x^3} - \sin x$

D. $y = cos x-{x^2}$
Câu 23:

Hàm số nào sau đây không là hàm số lẻ?

A. y=tan⁡x

B. y=cot⁡x

C. y=sin⁡x

D. y=cosx
Câu 24:

Điểm O (0;0) luôn thuộc đồ thị hàm số

A. y=cos⁡x

B. y=sin⁡x

C. y=cot⁡x

D. y=tanx−1
Câu 25:

Đồ thị hàm số y = tan x luôn đi qua điểm nào dưới đây?

A. $O(0;0)$

B. $M(0;1)$

C. $N\left( {\frac{\pi }{2};0} \right)$

D. $P(1;0)$
Câu 26:

Hàm số y = sin x nghịch biến trên khoảng nào dưới đây:

A. $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$

B. $\left( { - \pi;\frac{\pi }{2}} \right)$

C. $(0;π)$

D. $R$
Câu 27:

Hàm số y = cos x nghịch biến trên mỗi khoảng:

A. $\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)$

B. $\left( { - \pi + k2\pi ;k2\pi } \right)$

C. $R$

D. $\left( {k2\pi ;\pi + k2\pi } \right)$
Câu 28:

Hàm số nào sau đây có tập giá trị là R?

A. y=tan⁡2x

B. y=cos2x

C. y=sin2x

D. y=−sinx
Câu 29:

Tập giá trị của hàm số y = sin x là:

A. (−1;1)

B. [−1;1]

C. R

D. [0;1]
Câu 30:

Tập xác định của hàm số y = 2sin x là

A. [0;2].

B. [−2;2].

C. R

D. [−1;1]
Câu 31:

Hàm số y = cos x xác định trên:

A. $R \setminus \left\{ {k\pi ,k \in Z} \right\}$

B. $R \setminus \left\{ {\frac{{k\pi }}{2},k \in Z} \right\}$

C. $R \setminus \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}$

D. $R$
Câu 32:

Hàm số y = sin x có tập xác định là

A. $R \setminus \left\{ {k\pi ,k \in Z} \right\}$

B. $R \setminus \left\{ {\frac{{k\pi }}{2},k \in Z} \right\}$

C. $R \setminus \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}$

D. $R$
Câu 33:

Tìm điều kiện xác định của hàm số $y=\frac{1-3 \cos x}{\sin x}$

A. $x \neq k 2 \pi$

B. $x \neq \frac{k \pi}{2}$

C. $x \neq \frac{\pi}{2}+k \pi$

D. $x \neq k \pi$
Câu 34:

Tìm tập xác định D của hàm số $y=\cot x+\sin 5 x+\cos x$

A. $D=R \backslash\left\{\frac{\pi}{2}+k \pi, k \in Z\right\}$

B. $D=R \backslash\left\{\frac{\pi}{2}+k 2 \pi, k \in Z\right\}$

C. $D=R \backslash\{k \pi, k \in Z\}$

D. $D=R \backslash\{k 2 \pi, k \in Z\}$
Câu 35:

Hàm số $y=\frac{2 \sin x+1}{1-\cos x}$ xác định khi

A. $x \neq \frac{\pi}{2}+k 2 \pi$

B. $x \neq k \pi$

C. $x \neq k 2 \pi$

D. $x \neq \frac{\pi}{2}+k \pi$
Câu 36:

Cho $x, y, z>0 \text { và } x+y+z=\frac{\pi}{2}$ Tìm giá trị lớn nhất của $y=\sqrt{1+\tan x \cdot \tan y}+\sqrt{1+\tan y \cdot \tan z}+\sqrt{1+\tan z \cdot \tan x}$

A. $y_{\max }=1+2 \sqrt{2}$

B. $y_{\max }=3 \sqrt{3}$

C. $y_{\max }=2$

D. $y_{\max }=2 \sqrt{3}$
Câu 37:

Cho hàm số $y=\frac{1}{2-\cos x}+\frac{1}{1+\cos x} \text { vói } x \in\left(0 ; \frac{\pi}{2}\right)$ Kết luận nào sau đây là đúng?

A. $\min\limits _{\left(0 ; \frac{\pi}{2}\right)} y=\frac{4}{3}\,\, khi \,\,x=\frac{\pi}{3}+k \pi, k \in \mathbb{Z}$

B. $\min\limits _{\left(0 ; \frac{\pi}{2}\right)} y=\frac{2}{3}\,\, khi \,\,x=\frac{\pi}{3}$

C. $\min\limits _{\left(0 ; \frac{\pi}{2}\right)} y=\frac{2}{3}\,\, khi \,\,x=\frac{\pi}{3}+k 2 \pi, k \in \mathbb{Z}$

D. $\min\limits _{\left(0 ; \frac{\pi}{2}\right)} y=\frac{4}{3}\,\, khi \,\,x=\frac{\pi}{3}$
Câu 38:

Tìm giá trị lớn nhất của hàm số $y=\sqrt{1+\frac{1}{2} \cos ^{2} x}+\frac{1}{2} \sqrt{5+2 \sin ^{2} x}$ .

A. $1+\frac{\sqrt{5}}{2}$

B. $\frac{\sqrt{22}}{2}$

C. $\frac{\sqrt{11}}{2}$

D. $1+\sqrt{5}$
Câu 39:

Giá trị nhỏ nhất của hàm số $y=\sin x \sqrt{\cos x}+\cos x \sqrt{\sin x}$ là:

A. 0

B. $\sqrt{2}$

C. $\sqrt[4]{2}$

D. $\sqrt{6}$
Câu 40:

Giá trị lớn nhất của hàm số $y=\sin ^{4} x+\cos ^{4} x+\sin x \cos x$ là:

A. $\frac{9}{8}$

B. $\frac{5}{4}$

C. 1

D. $\frac{4}{3}$
Câu 41:

Hàm số $y=2 \cos x+\sin \left(x+\frac{\pi}{4}\right)$ đạt giá trị lớn nhất là

A. $5-2 \sqrt{2}$

B. $5+2 \sqrt{2}$

C. $\sqrt{5+2 \sqrt{2}}$

D. $\sqrt{5-2 \sqrt{2}}$
Câu 42:

Hàm số $y=4 \cot ^{2} 2 x-\frac{\sqrt{3}\left(1-\tan ^{2} x\right)}{\tan x}$ đạt giá trị nhỏ nhất là

A. 0

B. $3-2 \sqrt{3}$

C. $2-2 \sqrt{2}$

D. -1
Câu 43:

Tìm tập xác định D của hàm số $y=\sqrt{5+2 \cot ^{2} x-\sin x}+\cot \left(\frac{\pi}{2}+x\right)$

A. $D=\mathbb{R} \backslash\left\{\frac{k \pi}{2}, k \in \mathbb{Z}\right\}$

B. $D=\mathbb{R} \backslash\left\{-\frac{k \pi}{2}, k \in \mathbb{Z}\right\}$

C. $D=\mathbb{R}$

D. $D=\mathbb{R} \backslash\{k \pi, k \in \mathbb{Z}\}$
Câu 44:

Hàm số $y=\tan x+\cot x+\frac{1}{\sin x}+\frac{1}{\cos x}$ không xác định trong khoảng nào trong các khoảng sau đây?

A. $\left(k 2 \pi ; \frac{\pi}{2}+k 2 \pi\right)$

B. $\left(\pi+k 2 \pi ; \frac{3 \pi}{2}+k 2 \pi\right)$

C. $\left(\frac{\pi}{2}+k 2 \pi ; \pi+k 2 \pi\right)$

D. $(\pi+k 2 \pi ; 2 \pi+k 2 \pi)$
Câu 45:

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y=\frac{\sin x+\cos x}{2 \sin x-\cos x+3}$ lần lượt là:

A. $m=-1 ; M=\frac{1}{2}$

B. $m=-1 ; M=2$

C. $m=-\frac{1}{2} ; M=1$

D. $m=1 ; M=2$
Câu 46:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau $y=3(3 \sin x+4 \cos x)^{2}+4(3 \sin x+4 \cos x)+1$

A. $\min y=\frac{1}{3} ; \max y=96$

B. $\min y-\frac{1}{3} ; \max y=6$

C. $\min y=-\frac{1}{3} ; \max y=96$

D. $\min y=2 ; \max y=6$
Câu 47:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau $y=\frac{\sin ^{2} 2 x+3 \sin 4 x}{2 \cos ^{2} 2 x-\sin 4 x+2}$

A. $\min y=\frac{5-\sqrt{97}}{4}, \max y=\frac{5+\sqrt{97}}{4}$

B. $\min y=\frac{5-\sqrt{97}}{18}, \max y=\frac{5+\sqrt{97}}{18}$

C. $\min y=\frac{5-\sqrt{97}}{8}, \max y=\frac{5+\sqrt{97}}{8}$

D. $\min y=\frac{7-\sqrt{97}}{8}, \max y=\frac{7+\sqrt{97}}{8}$
Câu 48:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau $y=3 \cos x+\sin x-2$

A. $\min y=-2-\sqrt{5} ; \max y=-2+\sqrt{5}$

B. $\min y=-2-\sqrt{7} ; \max y=-2+\sqrt{7}$

C. $\min y=-2-\sqrt{3} ; \max y=-2+\sqrt{3}$

D. $\min y=-2-\sqrt{10} ; \max y=-2+\sqrt{10}$
Câu 49:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau $y=\frac{2 \sin ^{2} 3 x+4 \sin 3 x \cos 3 x+1}{\sin 6 x+4 \cos 6 x+10}$

A. $\min y=\frac{11-9 \sqrt{7}}{83} ; \max y=\frac{11+9 \sqrt{7}}{83}$

B. $\min y=\frac{22-9 \sqrt{7}}{11} ; \max y=\frac{22+9 \sqrt{7}}{11}$

C. $\min y=\frac{33-9 \sqrt{7}}{83} ; \max y=\frac{33+9 \sqrt{7}}{83}$

D. $\min y=\frac{22-9 \sqrt{7}}{83} ; \max y=\frac{22+9 \sqrt{7}}{83}$
Câu 50:

Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau $y=\frac{\sin 2 x+2 \cos 2 x+3}{2 \sin 2 x-\cos 2 x+4}$

A. $\min y=-\frac{2}{11} ; \max y=2$

B. $\min y=\frac{2}{11} ; \max y=3$

C. $\min y=\frac{2}{11} ; \max y=4$

D. $\min y=\frac{2}{11} ; \max y=2$