Trắc nghiệm Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán Lớp 12

Câu 1:

Một nhà sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dung tích 1000 cm³. Biết rằng bán kính của nắp đậy sao cho nhà sản xuất tiết kiệm nguyên vật liệu nhất có giá trị là a. Hỏi giá trị a gần với giá trị nào nhất dưới đây?

Câu 2:

Một con cá bơi ngược dòng để vượt một khoảng cách là 300km, vận tốc nước là 6(km/h). Vận tốc bơi của cá khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong t giờ được cho bởi công thức: E(v) =  c.v³.t, trong đó c là hằng số, E tính bằng Jun. Hỏi vận tốc bơi của cá khi nước đứng yên sao cho năng lượng tiêu hao ít nhất là bao nhiêu ?

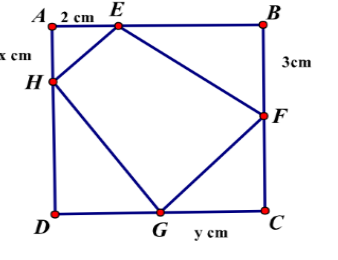
Câu 3:

Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng x + y để diện tích hình thang EFGH đạt giá trị nhỏ nhất.

Câu 4:

Giá trị lớn nhất của hàm số \(f(x) = \left| {{x^3} + 3{x^2} – 72x + 90} \right| + m\) trên đoạn \(\left[ { – 5;5} \right]\) là 2018. Trong các khẳng định dưới đây khẳng định nào đúng?

Câu 5:

Để giá trị lớn nhất của hàm số \(y = \left| {\sqrt {2x – {x^2}} – 3m + 4} \right|\) đạt giá trị nhỏ nhất thì m thỏa

Câu 6:

Cho hàm số \(f(x) = \left| {{x^4} – 8{x^2} – m} \right|.\) Có bao nhiêu giá trị nguyên của \(m \in {\rm{[}} – 50;50]\) sao cho với mọi số thực \(a, b, c \in {\rm{[}}0;3]\) thì \(f(a),{\rm{ }}f(b),{\rm{ }}f(c)\) là độ dài ba cạnh của một tam giác.

Câu 7:

Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{{{x^2} + mx + m}}{{x + 1}}} \right|\) trên \(\left[ {1;\,2} \right]\) bằng 2. Số phần tử của S là

Câu 8:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right)\). Hàm số \(y = f’\left( x \right)\) liên tục trên tập số thực và có đồ thị như hình vẽ.

Biết \(f\left( { – 1} \right) = \frac{{13}}{4},\,f\left( 2 \right) = 6\). Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(g\left( x \right) = {f^3}\left( x \right) – 3f\left( x \right)\) trên \(\left[ { – 1;2} \right]\) bằng:

Câu 9:

Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{{{x^2} + mx + m}}{{x + 1}}} \right|\) trên \(\left[ {1;2} \right]\) bằng 2. Số phần tử của tập S là

Câu 10:

Xét hàm số \(y = \left| {{x^2} + ax + b} \right|\), với a,b là tham số. Gọi M là giá trị lớn nhất của hàm số trên \(\left[ { – 1;3} \right]\). Khi M nhận giá trị nhỏ nhất có thể được, tính a + 2b.

Câu 11:

Cho hàm số \(y = {x^3} + 3m{x^2} + 3\left( {2m – 1} \right)x + 1\) (với m là tham số). Tìm tất cả các giá trị của tham số m để trên đoạn \(\left[ { – 2;0} \right]\) hàm số trên đạt giá trị lớn nhất bằng 6.

Câu 12:

Để giá trị lớn nhất của hàm số \(y = f\left( x \right) = \left| {{x^3} – 3x + 2m – 1} \right|\) trên đoạn \(\left[ {0;2} \right]\) là nhỏ nhất thì giá trị của m thuộc

Câu 13:

Cho hàm số \(y = {x^3} + 3m{x^2} + 3\left( {2m – 1} \right)x + 1\) (với m là tham số). Tìm tất cả các giá trị của tham số m để trên đoạn \(\left[ { – 2;0} \right]\) hàm số trên đạt giá trị lớn nhất bằng 6.

Câu 14:

Cho hàm số \(f\left( x \right)\) có đạo hàm là \(f’\left( x \right)\). Đồ thị hàm số \(y = f’\left( x \right)\) được cho như hình vẽ bên. Biết rằng \(f\left( 0 \right) + f\left( 2 \right) = f\left( 1 \right) + f\left( 3 \right)\). Giá trị lớn nhất của \(f\left( x \right)\) trên đoạn \(\left[ {0;3} \right]\) là

Câu 15:

Đồ thị hàm số \(y = f’\left( x \right)\) là đường cong nét đậm và \(y = g’\left( x \right)\) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của \(y = f’\left( x \right)\) và \(y = g’\left( x \right)\) trên hình vẽ lần lượt có hoành độ a,b,c. Tìm giá trị nhỏ nhất của hàm số \(h\left( x \right) = f\left( x \right) – g\left( x \right)\) trên đoạn \(\left[ {a;c} \right]\)?

Câu 16:

Tìm các giá trị nguyên dương \(n \ge 2\) để hàm số \(y = {\left( {2 – x} \right)^n} + {\left( {2 + x} \right)^n}\) với \(x \in \left[ { – 2;{\rm{ 2}}} \right]\) có giá trị lớn nhất gấp 8 lần giá trị nhỏ nhất.

Câu 17:

Biết hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có M và m lần lượt là GTLN, GTNN của hàm số trên đoạn \(\left[ {0;2} \right]\). Trong các hàm số sau, hàm số nào cũng có GTLN và GTNN tương ứng là M và m?.

Câu 18:

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \sqrt {1 – {x^2}} + 3\sqrt[3]{{{{\left( {1 – {x^2}} \right)}^2}}}\). Hỏi điểm \(A\left( {M;m} \right)\) thuộc đường tròn nào sau đây?

Câu 19:

Có tất cả bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số \(y = \left| {{x^2} – 2x + m} \right|\) trên đoạn \(\left[ { – 1;2} \right]\) bằng 5.

Câu 20:

Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho \(\mathop {\max }\limits_{\left[ { – 2;1} \right]} \left( {{x^4} – 6m{x^2} + {m^2}} \right) = 16\). Số phần tử của S là ?

Câu 21:

Giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(f\left( x \right) = 5\left( {\sqrt {x – 1} + \sqrt {3 – x} } \right) + \sqrt {\left( {x – 1} \right)\left( {3 – x} \right)} \) lần lượt là m và M, tính \(S = {m^2} + {M^2}\).

Câu 22:

Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = x\left( {2017 + \sqrt {2019 – {x^2}} } \right)\) trên tập xác định của nó. Tính M – m.

Câu 23:

Hàm số \(y = 4\sqrt {{x^2} – 2x + 3} + 2x – {x^2}\) đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là:

Câu 24:

Biết rằng phương trình \(\sqrt {2 – x} + \sqrt {2 + x} – \sqrt {4 – {x^2}} = m\) có nghiệm khi m thuộc \(\left[ {a;b} \right]\) với \(a, b \in \mathbb{R}\). Khi đó giá trị của \(T = \left( {a + 2} \right)\sqrt 2 + b\) là?

Câu 25:

Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số \(y = \frac{{x – {m^2} – 2}}{{x – m}}\) trên đoạn \(\left[ {0;4} \right]\) bằng – 1.

Câu 26:

Biết rằng giá trị lớn nhất của hàm số \(y = \left| {{x^2} + 2x + m – 4} \right|\) trên đoạn \(\left[ { – 2;\,1} \right]\) đạt giá trị nhỏ nhất, giá trị của tham số m bằng

Câu 27:

Cho hàm số \(y = \left| {{x^2} + 2x + a – 4} \right|\). Tìm a để giá trị lớn nhất của hàm số trên đoạn \(\left[ { – 2;1} \right]\) đạt giá trị nhỏ nhất?

Câu 28:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới. Xét hàm số \(g\left( x \right) = f\left( {2{x^3} + x – 1} \right) + m\). Tìm m để \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = – 10\).

Câu 29:

Cho hàm số \(y = \frac{{1 – m\sin x}}{{\cos x + 2}}\). Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn \(\left[ {0;10} \right]\) để giá trị nhỏ nhất của hàm số nhỏ hơn – 2?

Câu 30:

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Đồ thị của hàm số \(y = f’\left( x \right)\) như hình bên. Đặt \(g\left( x \right) = 2f\left( x \right) – {\left( {x + 1} \right)^2}\). Mệnh đề nào dưới đây đúng?

Câu 31:

Có một giá trị \({m_0}\) của tham số m để hàm số \(y = {x^3} + \left( {{m^2} + 1} \right)x + m + 1\) đạt giá trị nhỏ nhất bằng 5 trên đoạn \(\left[ {0;\,1} \right]\). Mệnh đề nào sau đây đúng?

Câu 32:

Cho x;y là hai số thực bất kỳ thuộc đoạn \(\left[ {1;3} \right].\) Gọi \(M,{\rm{ }}m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(S = \frac{x}{y} + \frac{y}{x}.\) Tính M + m.

Câu 33:

Cho hàm số \(y = \frac{{x + m}}{{x + 1}}\) (m là tham số thực) thoả mãn \(\mathop {\min }\limits_{\left[ {1\;;\;2} \right]} y + \mathop {{\rm{max}}}\limits_{\left[ {1\;;\;2} \right]} y = \frac{{16}}{3}\). Mệnh đề nào dưới đây đúng?

Câu 34:

Biết giá trị lớn nhất của hàm số \(y = \left| {\sqrt {4 – {x^2}} + x – \frac{1}{2}} \right| + m\) là 18. Mệnh đề nào sau đây đúng?

Câu 35:

Chohàm số \(y = \frac{1}{3}{x^3} + {m^2}x – 2{m^2} + 2m – 9,m\) là tham số. Gọi S là tập tất cả các giá trị của m sao cho giá trị lớn nhất của hàm số trên đoạn \(\left[ {0;3} \right]\) không vượt quá 3. Tìm m?

Câu 36:

Gọi m là giá trị để hàm số \(y = \frac{{x – {m^2}}}{{x + 8}}\) có giá trị nhỏ nhất trên \(\left[ {0;\;3} \right]\) bằng – 2. Mệnh đề nào sau đây là đúng?

Câu 37:

Hàm số \(f\left( x \right) = \frac{{mx + 5}}{{x – m}}\) có giá trị nhỏ nhất trên đoạn \(\left[ {0;1} \right]\) bằng – 7 khi

Câu 38:

Gọi m và M lần lượt là các giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = {{\rm{e}}^{2 – 3x}}\) trên đoạn \(\left[ {0;2} \right]\). Mối liên hệ giữa M và m là

Câu 39:

Số các giá trị tham số m để hàm số \(y = \frac{{x – {m^2} – 1}}{{x – m}}\) có giá trị lớn nhất trên \(\left[ {0;\,4} \right]\) bằng – 6 là

Câu 40:

Tìm tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số \(y = \frac{{x + 2{m^2} – m}}{{x – 3}}\) trên đoạn \(\left[ {0;1} \right]\) bằng – 2.

Câu 41:

Tìm x để hàm số \(y = \sqrt {x + 2} + \sqrt {6 – x} \) đạt giá trị lớn nhất?

Câu 42:

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = – 3 + \sqrt {4 – {x^2}} \) lần lượt là.

Câu 43:

M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = x + 1 + \sqrt {2 – {x^2}} \). Tính M – m?

Câu 44:

Tìm tập giá trị T của hàm số \(y = x + \sqrt {4 – {x^2}} .\).

Câu 45:

Cho hàm số \(f\left( x \right) = \frac{{x – {m^2}}}{{x + 8}},\) với m là tham số. Giá trị lớn nhất của m để \(\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = – 2\) là

Câu 46:

Cho hàm số \(y = \frac{{x + m}}{x}\) thỏa \(\mathop {\min }\limits_{\left[ {1;2} \right]} y + \mathop {\max }\limits_{\left[ {1;2} \right]} y = 8\), với m là tham số thực. Mệnh đề nào dưới đây đúng?

Câu 47:

Cho hàm số \(y = {x^3} – 3{x^2} – 9x + m\) có giá trị lớn nhất trên đoạn \(\left[ { – 2;0} \right]\) bằng 2, với m là tham số thực. Mệnh đề nào dưới đây đúng?

Câu 48:

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = – {x^2} – 1\). Với các số thực dương a, b thỏa mãn a < b, giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\) bằng.

Câu 49:

Có một giá trị \({m_0}\) của tham số m để hàm số \(y = {x^3} + \left( {{m^2} + 1} \right)x + m + 1\) đạt giá trị nhỏ nhất bằng 5 trên đoạn \(\left[ {0;1} \right]\). Mệnh đề nào sau đây là đúng?

Câu 50:

Gọi A, B là giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = \frac{{x + {m^2} + m}}{{x – 1}}\) trên đoạn \(\left[ {2;3} \right]\). Tìm tất cả các giá trị thực của tham số m để \(A + B = \frac{{13}}{2}\).