Để giá trị lớn nhất của hàm số \(y = f\left( x \right) = \left| {{x^3} – 3x + 2m – 1} \right|\) trên đoạn \(\left[ {0;2} \right]\) là nhỏ nhất thì giá trị của m thuộc
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXét hàm số \(y = g\left( x \right) = {x^3} – 3x + 2m – 1\) trên đoạn \(\left[ {0;2} \right]\), ta có:
\(y’ = 3{x^2} – 3,\,\,\,y’ = 0 \Leftrightarrow 3{x^2} – 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = – 1\\x = 1\end{array} \right.\)
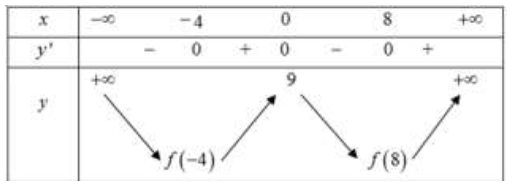
Bảng biến thiên của hàm số hàm số \(y = g\left( x \right) = {x^3} – 3x + 2m – 1\) trên đoạn \(\left[ {0;2} \right]\)
.png)
Ta luôn có: \(2m – 3 < 2m – 1 < 2m + 1 \Leftrightarrow g\left( 1 \right) < g\left( 0 \right) < g\left( 2 \right)\)
Suy ra: \(F = \mathop {\max }\limits_{\left[ {0;2} \right]} f\left( x \right) = \max \left\{ {\left| {2m – 3} \right|,\left| {2m + 1} \right|} \right\}\).
Nếu \(\left| {2m – 3} \right| \le \left| {2m + 1} \right| \Leftrightarrow {\left( {2m – 3} \right)^2} \le {\left( {2m + 1} \right)^2} \Leftrightarrow 8 \le 16m \Leftrightarrow m \ge \frac{1}{2}\) thì
\(F = \left| {2m + 1} \right| \ge \left| {2.\frac{1}{2} + 1} \right| \ge 2\).
Suy ra: \({F_{\min }} = 2 \Leftrightarrow m = \frac{1}{2}\).
Nếu \(\left| {2m – 3} \right| \ge \left| {2m + 1} \right| \Leftrightarrow {\left( {2m – 3} \right)^2} \ge {\left( {2m + 1} \right)^2} \Leftrightarrow 8 \ge 16m \Leftrightarrow m \le \frac{1}{2}\) thì
\(F = \left| {2m – 3} \right| = 3 – 2m \ge 3 – 2.\frac{1}{2} \ge 2\).
Suy ra:\({F_{\min }} = 2 \Leftrightarrow m = \frac{1}{2}\).
Vậy \(m \in \left( {0;1} \right)\).
Câu hỏi liên quan
-
Cho hàm số \(f(x)=\sin ^{3} x-3 \sin x+2 .\) Gọi và lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho.
Khi đó là \(M+2 m\) là? -
Giá trị lớn nhất của hàm số \(f ( x) = x³ - 3x + 3\) trên \(\left[ { - 1;\frac{3}{2}} \right]\)bằng
-
Giá trị lớn nhất của hàm số \(y = \sqrt { - {x^2} + 4x} \) là:
-
Cho hàm số \(f\left( x \right) = \frac{{2\sqrt x + m}}{{\sqrt {x + 1} }}\) với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3.
-
Hàm số \(y=\cos 2 x-4 \sin x+4\) có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \(\left[0 ; \frac{\pi}{2}\right]\) lần lượt là:
-
Cho hàm số \(y = \frac{{x + m}}{{x + 1}}\) (m là tham số thực) thoả mãn \(\mathop {\min }\limits_{\left[ {1\;;\;2} \right]} y + \mathop {{\rm{max}}}\limits_{\left[ {1\;;\;2} \right]} y = \frac{{16}}{3}\). Mệnh đề nào dưới đây đúng?
-
Cho hàm số \(y = \frac{{1 – m\sin x}}{{\cos x + 2}}\). Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn \(\left[ {0;10} \right]\) để giá trị nhỏ nhất của hàm số nhỏ hơn – 2?
-
Tìm giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} – 4x}}{{2x + 1}}\) trên đoạn \(\left[ {0;3} \right]\).
-
Hàm số \(y=x+\frac{1}{x}+x^{2}+\frac{1}{x^{2}}\) có giá trị nhỏ nhất, giá trị lớn nhất trên đoạn [1;3] là:
-
Hàm số \(y = {\left( {4 – {x^2}} \right)^2} + 1\) có giá trị lớn nhất trên đoạn \(\left[ { – 1;1} \right]\) là:
-
Tìm giá trị nhỏ nhất của hàm số \(y=f(x)=\sqrt{x-2}+\sqrt{8-x}\)
-
Hàm số \(y=\frac{x-1}{\sqrt{x^{2}+2}}\) đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [-3;0] lần lượt tại \(x_{1} ; x_{2}\) Khi đó \(x_{1} . x_{2}\) bằng:
-
Số nguyên nhỏ nhất của tham số để PT \({x^2} + \left( {m + 2} \right)x + 4 = \left( {m - 1} \right)\sqrt {{x^3} + 4x} \) có nghiệm là
-
Cho hàm số y=f(x) có bảng biến thiên như sau:
.PNG)
\(\text { Đặt } g(x)=[f(x)]^{3}-3[f(x)]^{2}\).Khẳng định nào sau đây đúng?
-
Hàm số \(y=\frac{1}{3} x^{3}-\frac{5}{2} x^{2}+6 x+1\) đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [1;3] tại điểm có hoành độ lần lượt là \(x_{1} ; x_{2}\) . Khi đó tổng \(x_{1} +x_{2}\) bằng
-
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x)=2 x-4 \sqrt{6-x}\) trên đoạn [-3 ; 6]. Tổng M+m có giá trị là:
-
Hàm số \(f(x)=2 \sin x+\sin 2 x\) trên đoạn \(\left[0 ; \frac{3 \pi}{2}\right]\) có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó M.m bằng
-
Giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} – 8{x^2} + 16x – 9\) trên đoạn \(\left[ {1;\,3} \right]\) là
-
Có tất cả bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số \(y = \left| {{x^2} – 2x + m} \right|\) trên đoạn \(\left[ { – 1;2} \right]\) bằng 5.
-
Tìm giá trị nhỏ nhất của hàm số \(y=\frac{x^2+3}{x-1}\)trên đoạn [2;4] .
