Tìm các giá trị nguyên dương \(n \ge 2\) để hàm số \(y = {\left( {2 – x} \right)^n} + {\left( {2 + x} \right)^n}\) với \(x \in \left[ { – 2;{\rm{ 2}}} \right]\) có giá trị lớn nhất gấp 8 lần giá trị nhỏ nhất.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(y’ = – n{\left( {2 – x} \right)^{n – 1}} + n{\left( {2 + x} \right)^{n – 1}} = n\left[ {{{\left( {2 + x} \right)}^{n – 1}} – {{\left( {2 – x} \right)}^{n – 1}}} \right]\)
\(y’ = 0 \Leftrightarrow {\left( {2 + x} \right)^{n – 1}} = {\left( {2 – x} \right)^{n – 1}}\)
Trường hợp 1. n chẵn \( \Leftrightarrow n – 1\) lẻ \( \Rightarrow y’ = 0 \Leftrightarrow \left( {2 + x} \right) = \left( {2 – x} \right) \Leftrightarrow x = 0\)
Trường hợp 2. n lẻ \( \Leftrightarrow n – 1\) chẵn \( \Rightarrow y’ = 0 \Leftrightarrow \left[ \begin{array}{l}2 + x = 2 – x\\2 + x = – 2 + x\end{array} \right. \Leftrightarrow x = 0\)
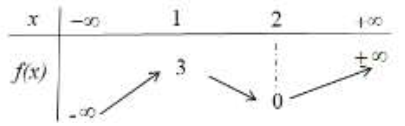
Ta có bảng biên thiên:
.png)
\(\mathop {{\rm{Min}}}\limits_{\left[ { – 2;2} \right]} = f\left( 0 \right) = {2^{n + 1}}; \mathop {{\rm{Max}}}\limits_{\left[ { – 2;2} \right]} = f\left( 2 \right) = f\left( { – 2} \right) = {4^n}\)
Theo bài ra ta có \({4^n} = {8.2^{n + 1}} \Leftrightarrow n = 4\).



.jpg.png)
.jpg.png)
.jpg.png)
.png)











