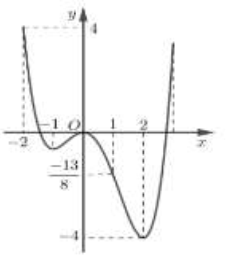
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left[ { – 4;4} \right]$, có các điểm cực trị trên $\left( { – 4;4} \right)$ là – 3, $– \frac{4}{3}$; 0; 2 và có đồ thị như hình vẽ. Đặt hàm số $y = g\left( x \right) = f\left( {{x^3} + 3x} \right) + m$ với m là tham số. Gọi ${m_1}$ là giá trị của m để $\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = 4, {m_2}$ là giá trị của m để $\mathop {\min g\left( x \right)}\limits_{\left[ { – 1;0} \right]} = – 2$. Giá trị của ${m_1} + {m_2}$ bằng

Giá trị lớn nhất của hàm số $y=2 \sin ^{4} x+\cos ^{2} x+3$ bằng

Hàm số $y=\sqrt{1+x^{2}}+\sqrt{1-x^{2}}$ đạt giá trị nhỏ nhất lần lượt tại hai điểm có hoành độ:

Giá trị lớn nhất của hàm số $y=-\frac{1}{3}x^3-\frac{1}{2}x^2+2x-1$ trên đoạn $\left[ {\frac{1}{2};2} \right]$ là

$\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{11x - 1}}{{2x + 3}}\text{ trên đoạn } \left[ { - 1;4} \right]$

Cho hàm số y=f(x) có đồ thị như hình dưới. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y=f(-2 x) \text { trên }\left[-1 ; \frac{1}{2}\right]$ Giá trị m+M bằng 

Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số $y = 2{x^3} + 3{x^2} – 12x + 1$ trên đoạn $\left[ { – 1;3} \right].$ Khi đó tổng M + m có giá trị là một số thuộc khoảng nào dưới đây?

Hàm số $y=\frac{x-1}{\sqrt{x^{2}+2}}$đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [-3 ; 0] lần lượt tại $x_{1} ; x_{2}$ . Khi đó $x_{1} . x_{2}$ bằng

Hàm số $y=\cos 2 x-4 \sin x+4$ có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn $\left[0 ; \frac{\pi}{2}\right]$ lần lượt là:

Giá trị nhỏ nhất của hàm số $y=\frac{1}{\sin x}$trên khoảng (0;π ) là:

Hàm số $y=\frac{x^{2}-2}{\sqrt{x^{2}+1}}$ có giá trị nhỏ nhất bằng

Cho đồ thị hàm số $y = f\left( x \right)$ như hình vẽ bên dưới. Biết rằng m là tham số thực, để giá trị nhỏ nhất của hàm số $g\left( x \right) = f\left( {2x + 3} \right) + {x^2} – 4mx + 4{m^2} – 1$ bằng – 4 thì tham số m bằng

Giá trị lớn nhất của hàm số $y=2 \sin ^{2} x+2 \sin x-1$ bằng

Hàm số $y=\sin x+1$ đạt giá trị lớn nhất trên đoạn $\left[-\frac{\pi}{2} ; \frac{\pi}{2}\right]$ bằng

Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên trên đoạn $\left[ { – 1;4} \right]$ như sau:

Giá trị lớn nhất của hàm số $y = \left| {f\left( x \right)} \right|$ trên đoạn đoạn $\left[ { – 1;4} \right]$ bằng

Một trang chữ của một quyển sách tham khảo Văn học cần diện tíc 384 cm² . Biết rằng trang giấy được canh lề trái là 2 cm , lề phải là 2 cm , lề trên 3 cm và lề dưới là 3 cm . Tìm chiều dài và chiều rộng của trang sách để trang sách có diện tích nhỏ nhất

Giá trị lớn nhất của hàm số $y=e^{x}+4 e^{-x}+3 x$ trên đoạn [1 ; 2] bằng

Cho hàm số y = x³- 3x+ 1. Tìm tìm tập hợp tất cả giá trị m > 0, để giá trị nhỏ nhất của hàm số trên D = [m+ 1; m+ 2] luôn bé hơn 3 là:

Hàm số $y=\sqrt{x^{2}+1}+x^{2}$ có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1;1] lần lượt là:

Giá trị lớn nhất của hàm số $y = \frac{{3x + 2}}{{x + 1}}$ trên $\left[ {0;\,2} \right]$ bằng

Cho hàm số $y=\sqrt{x^{2}-x+1}$ . Khẳng định nào sau đây đúng: