Trắc nghiệm Hàm số liên tục Toán Lớp 11
-
Câu 1:
Cho phương trình x5−5x−3=0, điều nào sau đây không đúng?
A. Phương trình có nghiệm
B. Phương trình có nghiệm thuộc (2;3)
C. Phương trình có nghiệm thuộc (−1;0)
D. Phương trình có nghiệm thuộc (0;2).
-
Câu 2:
Phương trình nào sau đây vô nghiệm ?
A. x4−2x2−1=0
B. x4+x2sinx+2=0
C. x3-3sin2x=0
D. xsin3x+cosx=0
-
Câu 3:
Phương trình xcosx−x2+1=0 có nghiệm thuộc khoảng nào?
A. (−4;−3)
B. (0;1)
C. (1;2)
D. (3;4)
-
Câu 4:
Cho phương trình mx3−x+1=0. Điều nào sau đây đúng?
A. Phương trình vô nghiệm
B. Phương trình luôn có ba nghiệm phân biệt
C. Phương trình có ít nhất một nghiệm
D. Phương trình có ít nhất hai nghiệm
-
Câu 5:
Cho phương trình xsinx+x2−3=0. Nhận xét nào sau đây không đúng?
A. Phương trình có nghiệm thuộc (−3;3)
B. Phương trình có nghiệm thuộc (−3;0)
C. Phương trình có nghiệm thuộc (0;3)
D. Phương trình có nghiệm thuộc (3;4)
-
Câu 6:
Phương trình x2−4sinx+1=0 có nghiệm thuộc khoảng?
A. (0;π2)(0;π2)
B. (π;3π2)(π;3π2)
C. (−2π;−π)(−2π;−π)
D. (2π;3π)(2π;3π)
-
Câu 7:
Phương trình nào sau đây có nghiệm trên R?
A. x2+1=0x2+1=0
B. x4+2x2+3=0x4+2x2+3=0
C. x3−3x+21=0x3−3x+21=0
D. x6−4x3+5=0x6−4x3+5=0
-
Câu 8:
Phương trình x3−3x2+1=0 có nghiệm thuộc khoảng ?
A. (5;7)
B. (3;4)
C. (−1;0)
D. (9;11)
-
Câu 9:
Phương trình x4+3x3−3=0 có nghiệm trên khoảng nào sau đây?
A. (3;1)
B. (0;1)
C. (1;2)
D. (2;3)
-
Câu 10:
Cho các số thực a, b, c thỏa mãn c2 + a = 18 vàlimx→+∞(√ax2+bx−cx)=−2limx→+∞(√ax2+bx−cx)=−2. Tính P = a + b + 5c
A. 18
B. 12
C. 9
D. 5
-
Câu 11:
Đặt f(n)=(n2+n+1)2+1.f(n)=(n2+n+1)2+1. Xét dãy số (un ) sao cho un=f(1).f(3).f(5)...f(2n−1)f(2).f(4).f(6)...f(2n)un=f(1).f(3).f(5)...f(2n−1)f(2).f(4).f(6)...f(2n). ) Tínhlimn√unlimn√un
A. limn√un=√2.limn√un=√2.
B. limn√un=1√3.limn√un=1√3.
C. limn√un=√3.limn√un=√3.
D. limn√un=1√2.limn√un=1√2.
-
Câu 12:
Tính giới hạn: lim[(1−122)(1−132)...(1−1n2)]lim[(1−122)(1−132)...(1−1n2)]
A. 1
B. 0,5
C. 3
D. 1,5
-
Câu 13:
Cho hàm số f(x)={−xcosx khi x<0x21+x khi 0≤x<1x3 khi x≥1. Hàm số f(x) liên tục tại:
A. Mọi điểm x∈R
B. Mọi điểm trừ x=1
C. Mọi điểm trừ x=0
D. Mọi điểm trừ x=2.
-
Câu 14:
Tính tổng S gồm tất cả các giá trị m để hàm số f(x)={x2+x khi x<12 khi x=1 liên tục tại x=1m2x+1 khi x>1
A. S=-1
B. S=0
C. S=1
D. S=2
-
Câu 15:
Số điểm gián đoạn của hàm số h(x)={2x khi x<0x2+1 khi 0≤x≤23x−1 khi x>2
A. 1
B. 2
C. 3
D. 0
-
Câu 16:
Cho hàm số f(x)={x2−1x−1 khi x<3,x≠14 khi x=1√x+1 khi x≥3. Hàm số f(x) liên tục tại:
A. Mọi điểm thuộc R .
B. Mọi điểm trừ x=1
C. Mọi điểm trừ x=3
D. Mọi điểm trừ x=1 và x=3
-
Câu 17:
Cho hàm số f(x)={x2x khi x<1,x≠00 khi x=0√x khi x≥1. Hàm số f(x) liên tục tại:
A. mọi điểm thuộc R
B. mọi điểm trừ x=1
C. mọi điểm trừ x=0
D. mọi điểm trừ x=0 và x=1.
-
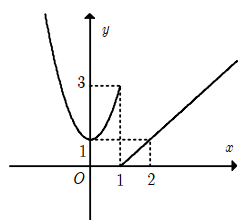
Câu 18:
Hàm số f(x) có đồ thị như hình bên không liên tục tại điểm có hoành độ là bao nhiêu?
A. x=0
B. x=1
C. x=2
D. x=3
-
Câu 19:
Tìm giá trị lớn nhất của a để hàm số f(x)={3√3x+2−2x−2 khi x>2a2x+14 khi x≤2 liên tục tại x=2.
A. amax=3.
B. amax=0.
C. amax=1.
D. amax=2.
-
Câu 20:
Tìm giá trị nhỏ nhất của a để hàm số f(x)={x2−5x+6√4x−3−x khi x>31−a2x khi x≤3 liên tục tại x = 3 .
A. −2√3
B. 2√3
C. −43
D. 43
-
Câu 21:
Biết rằng f(x)={x2−1√x−1 khi x≠1a khi x=1 liên tục trên đoạn [0;1] (với a là tham số). Khẳng định nào dưới đây về giá trị a là đúng?
A. a là một số nguyên.
B. a là một số vô tỉ.
C. a>5.
D. a<0.
-
Câu 22:
Có bao nhiêu giá trị của tham số a để hàm số f(x)={x2−3x+2|x−1| khi x≠1a khi x=1 liên tục trên R.
A. 0
B. 1
C. 2
D. 3
-
Câu 23:
Biết rằng hàm số f(x)={√x khi x∈[0;4]1+m khi x∈(4;6] liên tục trên [0;6]. Khẳng định nào sau đây đúng?
A. m<2
B. 2≤m<3
C. 3<m<5
D. m≥5
-
Câu 24:
Có bao nhiêu giá trị thực của tham số m để hàm số f(x)={m2x2 khi x≤2(1−m)x khi x>2 liên tục trên R ?
A. 0
B. 1
C. 2
D. 3
-
Câu 25:
Số điểm gián đoạn của hàm số f(x)={0,5 khi x=−1x(x+1)x2−1 khi x≠−1,x≠11 khi x=1 là:
A. 0
B. 1
C. 2
D. 3
-
Câu 26:
Biết rằng limx→0sinxx=1 .Tìm giá trị thực của tham số m để hàm số f(x)={1+cosx(x−π)2 khi x≠πm khi x=π liên tục tại x=π.
A. m=π2
B. m=−π2
C. m=12
D. m=−12
-
Câu 27:
Biết rằng limx→0sinxx=1. Tìm giá trị thực của tham số m để hàm số f(x)={sinπxx−1 khi x≠1m khi x=1 liên tục tại x=1 .
A. m=π.
B. m=−π.
C. m=-1.
D. m=1.
-
Câu 28:
Biết rằng limx→0sinxx=1. Hàm số f(x)={tanxx khi x≠00 khi x=0 liên tục trên khoảng nào sau đây?
A. (0;π2).
B. (−∞;π4).
C. (−π4;π4).
D. (−∞;+∞).
-
Câu 29:
Tìm giá trị thực của tham số m để hàm số f(x)={x2sin1x khi x≠0m khi x=0 liên tục tại x=0.
A. m=-1
B. m=0
C. m=1
D. m=-2
-
Câu 30:
Biết rằng hàm số f(x)={3−x√x+1−2 khi x≠3m khi x=3 liên tục tại x = 3 (với m là tham số). Khẳng định nào dưới đây đúng?
A. m∈(−3;0).
B. m≤−3.
C. m∈[0;5)
D. m∈[5;+∞) .
-
Câu 31:
Tìm giá trị thực của tham số k để hàm số y=f(x)={√x−1x−1 khi x≠1k+1 khi x=1 liên tục tại x=1
A. k=−12
B. k=−1√2
C. k=12
D. k=1√2
-
Câu 32:
Tìm giá trị thực của tham số m để hàm số f(x)={x3−x2+2x−2x−1 khi x≠13x+m khi x=1 liên tục tại x=1
A. m=0
B. m=1
C. m=2
D. Không tìm được m.
-
Câu 33:
Tìm giá trị thực của tham số m để hàm số f(x)={x2−x−2x−2 khi x≠2m khi x=2 liên tục tại x=2.
A. m=3
B. m=4
C. m=5
D. m=6
-
Câu 34:
Xác định a, b để hàm số f(x)={x3−3x2+2xx(x−2) khi x(x−2)≠0a khi x=2b khi x=0 liên tục trên R.
A. {a=1b=−1
B. {a=2b=1
C. {a=−1b=−1
D. Không tìm được giá trị của a, b.
-
Câu 35:
Xác định a,b đểhàm số f(x)={sinx khi |x|≤π2ax+b khi |x|>π2liên tục trên R.
A. {a=2πb=0
B. {a=2πb=π
C. {a=2πb=0
D. Không tìm được giá trị a,b.
-
Câu 36:
Tìm a để hàm số f(x)={√3x+1−2x2−1 khi x>1a(x2−2)x−3 khi x≤1 sau liên tục tại x=1.
A. a=√32
B. a=±√3
C. a=34
D. a=-1
-
Câu 37:
Tìm a để hàm số f(x)={√4x+1−1ax2+(2a+1)x khi x≠03 khi x=0 liên tục tại x=0.
A. a=√6
B. a=−16
C. a=−13
D. Không tìm được giá trị của a.
-
Câu 38:
Tìm a để hàm số f(x)={x+2a khi x<0x2+x+1 khi x≥0 liên tục tại x=0.
A. a=12
B. a=1√2
C. a=13
D. a=1√3
-
Câu 39:
Chọn giá trị f(0) để hàm số f(x)=3√2x+8−2√3x+4−2 liên tục tại điểm x=0.
A. 29
B. 1
C. -2
D. −19
-
Câu 40:
Chọn giá trị f(0) để hàm số f(x)=√2x+1−1x(x+1) liên tục tại điểm x=0.
A. f(0)=1
B. f(0)=-1
C. f(0)=2
D. f(0)=-2
-
Câu 41:
Tìm a để hàm số f(x)={x4−5x2+4x3−8 khi x<2ax2+x+1 khi x≥2 liên tục tại x=2.
A. Không tìm được giá trị của a.
B. a=12
C. Với mọi a.
D. a=−12
-
Câu 42:
Tìm a để hàm số f(x)={3√4x−2x−2 khi x≠2a khi x=2 liên tục tại x=2.
A. a=−13
B. a=13
C. a=0.
D. Không tìm được giá trị của a.
-
Câu 43:
Tìm già trị của m để hàm số f(x)={x2+x−2x−1 nếu x≠1m nếu x=1 liên tục tại x = 1.
A. Không tồn tại m.
B. Với mọi m.
C. m=3.
D. m=2.
-
Câu 44:
Tìm các giá trị của tham số m để hàm số f(x)={x2−3x+2x2−x nếu x<1mx+m+1 nếu x≥1 liên tục trên ℝ .
A. m=-1
B. m=-2
C. m=-3
D. m=-4
-
Câu 45:
Tìm m để hàm số f(x)={√x−1x2−1 nếu x≠1m2x nếu x=1 liên tục tại x = 1.
A. m=±12
B. m=−12
C. m=-1
D. m=1
-
Câu 46:
Tìm các giá trị của a và b để hàm số f(x)={ax−b nếu x≤13x nếu 1<x<2bx2−a nếu x≥2 liên tục tại x=1 và gián đoạn tại x=2.
A. {a=b+3b≠3
B. a=b≠3
C. {a=3b=3
D. {a=b+3b≠−1
-
Câu 47:
Tìm điều kiện của a và b để hàm số f(x)={ax−b nếux≤13x nếu 1<x<2bx2−a nếu x≥2 liên tục tại x=1.
A. 2a+b=1
B. a=1, b=2
C. a-b=3
D. a+b=-1
-
Câu 48:
Tìm số thực a sao cho hàm số f(x)={a2x2 nếu x≤2(1−a)x nếu x>2 liên tục trên R
A. a=−1,a=12
B. a=−1
C. a=32
D. a=2
-
Câu 49:
Cho hàm số f(x)={1x−1−3x3−1 nếu x>1mx+2 nếu x≤1.. Với giá trị nào của tham số m thì hàm số f(x) liên tục tại x = 1 .
A. m=1
B. m=-1
C. m=0
D. m=2
-
Câu 50:
Tìm già trị của m để hàm số f(x)={x2−x−2x−2 nếu x≠2m nếu x=2 liên tục tại x = 2.
A. m=1
B. m=2
C. m=3
D. m=4