Trắc nghiệm Hàm số liên tục Toán Lớp 11
-
Câu 1:
Tìm các giá trị của tham số m để hàm số \(f(x)=\left\{\begin{array}{ccc} \frac{x^{2}-3 x+2}{x^{2}-2 x} & \text { nếu } & x<2 \\ m x+m+1 & \text { nếu } & x \geq 2 \end{array}\right.\) liên tục trên \(\mathbb{R}\).
A. \(m=-\frac{1}{6} .\)
B. Với mọi m.
C. Không tìm được m.
D. m=1
-
Câu 2:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{a x^{2}-(a-2) x-2}{\sqrt{x+3}-2} & \text { khi } x \neq 1 \\ 8+a^{2} & \text { khi } x=1 \end{array}\right.\). Có tất cả bao nhiêu giá trị của a để hàm số liên tục tại x=1?
A. 0
B. 1
C. 2
D. 3
-
Câu 3:
Tìm m để các hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sqrt[3]{x-2}+2 x-1}{x-1} & \text { khi } x \neq 1 \\ 3 m-2 & \text { khi } x=1 \end{array}\right.\) liên tục trên \(\mathbb{R}\)?
A. \(m=-1\)
B. \(m=\frac{4}{3}\)
C. \(m=1\)
D. \(m=0\)
-
Câu 4:
Cho hàm số \(f(x)=\left\{\begin{array}{lr} \frac{\sqrt{4 x+1}-1}{a x^{2}+(2 a+1) x} & \text { khi } x \neq 0 \\ 3 & \text { khi } x=0 \end{array}\right.\) Tìm giá trị của a để hàm số f(x) liên tục tại \(x_{0}=0\)
A. \(a=\frac{1}{2}\)
B. \(a=-\frac{1}{6}\)
C. \(a=\frac{1}{4}\)
D. \(a=1\)
-
Câu 5:
Hàm số \(f(x)=\left\{\begin{array}{ll} 3 & \text { khi } x=-1 \\ \frac{x^{4}+x}{x^{2}+x} & \text { khi } x \neq-1, x \neq 0 \\ 1 & \text { khi } x=0 \end{array}\right.\) liên tục tại:
A. Mọi điểm trừ x x = = 0, 1.
B. Mọi điểm x ∈ ℝ
C. Mọi điểm trừ x = -1.
D. Mọi điểm trừ x = 0.
-
Câu 6:
Biết rằng\(\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\). Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} \frac{1+\cos x}{(x-\pi)^{2}} & \text { khi } x \neq \pi \\ m & \text { khi } x=\pi \end{array}\right.\) liên tục tại \(x=\pi\)?
A. \(m=\frac{\pi}{2} .\)
B. \(m=-\frac{\pi}{2} .\)
C. \(m=\frac{1}{2}\)
D. \(m=-\frac{1}{2}\)
-
Câu 7:
Biết rằng\(\lim\limits _{x \rightarrow 0} \frac{\sin x}{x}=1\) . Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sin \pi x}{x-1} & \text { khi } x \neq 1 \\ m & \text { khi } x=1 \end{array}\right.\) liên tục tại x = 1 ?
A. m=-1
B. m=0
C. \(m=\pi\)
D. \(m=-\pi\)
-
Câu 8:
Biết rằng \(\lim\limits _{x \rightarrow 0} \frac{\sin x}{x}=1\). Hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\tan x}{x} & \text { khi } x \neq 0 \\ 0 & \text { khi } x=0 \end{array}\right.\) liên tục trên khoảng nào sau đây?
A. \(\left(0 ; \frac{\pi}{2}\right) .\)
B. \(\left(-\infty ; \frac{\pi}{4}\right) .\)
C. \(\left(-\frac{\pi}{4} ; \frac{\pi}{4}\right) .\)
D. \((-\infty ;+\infty)\)
-
Câu 9:
Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} x^{2} \sin \frac{1}{x} & \text { khi } x \neq 0 \\ m & \text { khi } x=0 \end{array}\right.\) liên
tục tại x = 0.A. \(m \in(-2 ;-1) . \)
B. \(m \leq-2 .\)
C. \(m \in[-1 ; 7) .\)
D. \(m \in[7 ;+\infty) .\)
-
Câu 10:
Biết rằng hàm số \(f(x)=\left\{\begin{array}{ll} \frac{3-x}{\sqrt{x+1}-2} & \text { khi } x \neq 3 \\ m & \text { khi } x=3 \end{array}\right.\) liên tục tại x = 3 (với m là tham số). Khẳng định nào dưới đây đúng?
A. \(m \in(-3 ; 0) . \)
B. \(m \leq-3 . \)
C. \(m \in[0 ; 5) . \)
D. \(m \in[5 ;+\infty) .\)
-
Câu 11:
Tìm giá trị thực của tham số k để hàm số \(y=f(x)=\left\{\begin{array}{ll} \frac{\sqrt{x}-1}{x-1} & \text { khi } x \neq 1 \\ k+1 & \text { khi } x=1 \end{array}\right.\) liên tục tại x = 1.
A. \(k=\frac{1}{2} \text { . }\)
B. \(k=-\frac{1}{2} \text { . }\)
C. \(k=0\)
D. \(k=1\)
-
Câu 12:
Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x^{3}-x^{2}+2 x-2}{x-1} & \text { khi } x \neq 1 \\ 3 x+m & \text { khi } x=1 \end{array}\right.\) liên tục tại x = 1.
A. m=0
B. m=1
C. m=2
D. m=3
-
Câu 13:
Tìm giá trị thực của tham số m để hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x^{2}-x-2}{x-2} & \text { khi } x \neq 2 \\ m & \text { khi } x=2 \end{array}\right.\) liên tục tại x=2
A. m=1
B. m=2
C. m=3
D. m=4
-
Câu 14:
Cho hàm số f (x) xác định và liên tục trên \((-4 ;+\infty) \text { với } f(x)=\frac{x}{\sqrt{x+4}-2}\) với x ≠ 0 . Tính f(0)?
A. 2
B. 3
C. 4
D. 0
-
Câu 15:
Cho hàm số f(x) xác định và liên tục trên [-3;3] với \(f(x)=\frac{\sqrt{x+3}-\sqrt{3-x}}{x}\)với x ≠ 0 . Tính f(x)?
A. \(\frac{\sqrt{3}}{3}\)
B. \(-\frac{\sqrt{3}}{3}\)
C. 0
D. 1
-
Câu 16:
Cho hàm số f(x) xác định và liên tục trên \(\mathbb{R} \text { với } f(x)=\frac{x^{2}-3 x+2}{x-1}\) với mọi \(x \neq 1 . \text { Tính } f(1)\).
A. 1
B. 2
C. 3
D. -1
-
Câu 17:
\(\text { Hàm số } f(x)=\frac{x^{3}+x \cos x+\sin x}{2 \sin x+3} \text { liên tục trên: }\)
A. \([-1 ; 1]\)
B. \([1 ; 5]\)
C. \(\left(\frac{3}{2} ;+\infty\right)\)
D. \(\mathbb{R}\)
-
Câu 18:
\(\text { Hàm số } f(x)=\sqrt{3-x}+\frac{1}{\sqrt{x+4}} \text { liên tục trên: }\)
A. \(\left[\begin{array}{llll} -4 ; 3] . \end{array}\right.\)
B. \([-4 ; 3) \)
C. \((-4 ; 3] . \)
D. \([-\infty ;-4] \cup[-3 ;+\infty) .\)
-
Câu 19:
Cho hàm số \(f(x)=\left\{\begin{array}{l} \frac{x^{3}-8}{x-2} \text { khi } x \neq 2 \\ m x+1 \text { khi } x=2 \end{array}\right.\). Tìm tất cả các giá trị của tham số thực m để hàm số liên tục tại x = 2
A. \(m=\frac{11}{2}\)
B. \(m=\frac{13}{2}\)
C. \(m=\frac{15}{2}\)
D. \(m=\frac{17}{2}\)
-
Câu 20:
Cho hàm số \(f(x)=\left\{\begin{array}{l} 3 x+2 \text { khi } x<-1 \\ x^{2}-1 \text { khi } x \geq-1 \end{array}\right.\). Chọn khẳng định đúng trong các khẳng định sau.
A. f(x) liên tục trên \(\begin{aligned} &\mathbb{R} \end{aligned}\)
B. f(x) liên tục trên \((-\infty ;-1]\)
C. f(x) liên tục trên \([-1 ;+\infty)\)
D. f(x) liên tục tại x=1
-
Câu 21:
Cho hàm số \(\begin{equation} f(x)=\frac{x-2}{x^{2}-3 x+2} \end{equation}\) . Hàm số liên tục trên
A. \((-\infty ; 1) \text { và }(1 ;+\infty)\)
B. \(\mathbb{R}\)
C. \(\begin{array}{l} (-\infty ; 2) \text { và }(2 ;+\infty) \end{array}\)
D. \((-\infty ; 1),(1 ; 2) \text { và }(2 ;+\infty)\)
-
Câu 22:
Cho hàm số \(\begin{equation} f(x)=\frac{x^{2}+1}{x^{2}+5 x+6} \end{equation}\). Hàm số f (x) liên tục trên khoảng nào sau đây?
A. \(\begin{equation} \begin{aligned} &(-\infty ; 3) . \end{aligned} \end{equation}\)
B. \((2 ; 3) .\)
C. \((-3 ; 2) \)
D. \((-3 ;+\infty) \)
-
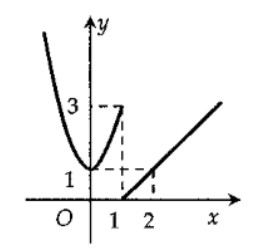
Câu 23:
Hàm số y=f(x) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
A. 0
B. 1
C. 2
D. 3
-
Câu 24:
Phương trình x4 - 3x2 + 1 = 0
A. Không có nghiệm trong (-1; 3)
B. Không có nghiệm trong (0; 1)
C. Có ít nhất hai nghiệm
D. Chỉ có một nghiệm duy nhất
-
Câu 25:
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^2} + 3x + 2}}{{{x^2} + x}}\,neu\,x \ne - 1\\3x + a\,neu\,x = - 1\end{array} \right.\)
Với giá trị nào của tham số a thì hàm số f(x) liên tục tại x = -1?
A. a = 2
B. a = 4
C. a = 3
D. a = 6
-
Câu 26:
Cho hàm số f(x) xác định trên khoảng K chứa a. Hàm số f(x) liên tục tại x = a nếu:
A. \(f\left( x \right)\) có giới hạn hữu hạn khi \(x \to a\)
B. \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = + \infty \)
C. \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = a\)
D. \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = f\left( a \right)\)
-
Câu 27:
Tìm giá trị của tham số \(m\) để hàm số
\(f\left( x \right) = \left\{ \matrix{
{{\sqrt x - 1} \over {{x^2} - 1}},\,\,{\rm{ nếu }}\,\,x \ne 1 \hfill \cr
{m^2}{\rm{ ,\,\, nếu }}\,\,x = 1 \hfill \cr} \right.\) liên tục trên \(\left( {0; + \infty } \right)\).A. \(m = \pm \dfrac{7}{2}\).
B. \(m = \pm \dfrac{5}{2}\).
C. \(m = \pm \dfrac{3}{2}\).
D. \(m = \pm \dfrac{1}{2}\).
-
Câu 28:
Cho hàm số \(f(x)=2 \sin x+3 \tan 2 x\). Khẳng định nào sau đây đúng nhất?
A. Hàm số liên tục trên \(\mathbb{R}\)
B. Hàm số liên tục tại mọi điểm.
C. \(\operatorname{TXĐ}: D=\mathbb{R} \backslash\left\{\frac{\pi}{2}+k \frac{\pi}{2}, k \in \mathbb{Z}\right\}\)
D. Hàm số gián đoạn tại các điểm \(x=\frac{\pi}{4}+k \frac{\pi}{2}, k \in \mathbb{Z}\)
-
Câu 29:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} a^{2} x^{2} \,\,\,\,\,\,\,\,\,\,\,\,, x \leq \sqrt{2}, a \in \mathbb{R} \\ (2-a) x^{2}, x>\sqrt{2} \end{array}\right.\). Giá trị của a để f (x) liên tục trên \(\mathbb{R}\) là
A. 1 và 2.
B. -1 và -2.
C. 1 và -2.
D. -1 và 2.
-
Câu 30:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\tan x}{x}, & x \neq 0 \wedge x \neq \frac{\pi}{2}+k \pi, k \in \mathbb{Z} \\ 0 & , x=0 \end{array}\right.\). Hàm số y=f(x) liên tục trên các khoảng
nào sau đây?A. \(\left(0 ; \frac{\pi}{2}\right)\)
B. \(\left(-\infty ; \frac{\pi}{4}\right)\)
C. \(\left(-\frac{\pi}{4} ; \frac{\pi}{4}\right)\)
D. \((-\infty ;+\infty)\)
-
Câu 31:
Cho hàm số \(f(x)=\left\{\begin{array}{l} \frac{\sqrt[3]{x}-1}{\sqrt{x}-1} \quad \text { khi } x>1 \\ \frac{\sqrt[3]{1-x}+2}{x+2} \text { khi } x \leq 1 \end{array}\right.\). Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên \(\mathbb{R}\)
B. Hàm số không liên tục trên \(\mathbb{R}\)
C. Hàm số không liên tục trên \((1:+\infty)\)
D. Hàm số gián đoạn tại các điểm x=1
-
Câu 32:
Cho hàm số \(f(x)=\left\{\begin{array}{cc} \frac{x^{2}-5 x+6}{2 x^{3}-16} & \text { khi } x<2 \\ 2-x & \text { khi } x \geq 2 \end{array}\right.\). Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục trên \(\mathbb{R}\)
B. Hàm số liên tục tại mọi điểm.
C. Hàm số không liên tục trên \((2:+\infty)\)
D. Hàm số gián đoạn tại điểm x=2
-
Câu 33:
Cho hàm số \(f(x)=\frac{x^{2}+1}{x^{2}+5 x+6}\).Khi đó hàm số \(f(x)\) liên tục trên các khoảng nào sau đây?
A. \((-3 ; 2)\)
B. \((-2 ;+\infty)\)
C. \((-\infty ; 3)\)
D. \((2 ; 3)\)
-
Câu 34:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{3-\sqrt{9-x}}{x} & , 0<x<9 \\ m & , x=0 \\ \frac{3}{x} & , x \geq 9 \end{array}\right.\). Tìm m để f(x) liên tục trên \([0 ;+\infty)\) là?
A. \(\frac{1}{3}\)
B. \(\frac{1}{2}\)
C. \(\frac{1}{6}\)
D. 1
-
Câu 35:
Tìm a để các hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sqrt{3 x+1}-2}{x^{2}-1} & \text { khi } x>1 \\ \frac{a\left(x^{2}-2\right)}{x-3} & \text { khi } x \leq 1 \end{array}\right.\)liên tục tại x=1
A. \(\frac{1}{2}\)
B. \(\frac{1}{4}\)
C. \(\frac{3}{4}\)
D. 1
-
Câu 36:
Tìm a để các hàm số \(f(x)=\left\{\begin{array}{lr} \frac{\sqrt{4 x+1}-1}{a x^{2}+(2 a+1) x} & \text { khi } x \neq 0 \\ 3 & \text { khi } x=0 \end{array}\right.\) liên tục tại x=0
A. \(\frac{1}{2}\)
B. \(\frac{1}{4}\)
C. \(-\frac{1}{6}\)
D. 1
-
Câu 37:
Tìm a để các hàm số \(f(x)=\left\{\begin{array}{c} x+2 a \text { khi } x<0 \\ x^{2}+x+1 \text { khi } x \geq 0 \end{array}\right.\) liên tục tại x=0.
A. \(\frac{1}{2}\)
B. \(\frac{1}{4}\)
C. 0
D. 1
-
Câu 38:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x^{2}-x-2}{\sqrt{x-2}}+2 x & \text { khi } x>2 \\ x^{2}-x+3 & \text { khi } x \leq 2 \end{array}\right.\). Khẳng định nào sau đây đúng nhất?
A. Hàm số liên tục tại \(x_{0}=2\)
B. Hàm số liên tục tại mọi điểm.
C. Hàm số không liên tục tại \(x_{0}=2\).
D. Tất cả đều sai
-
Câu 39:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sqrt[3]{x}-1}{x-1} & \text { khi } x \neq 1 \\ \frac{1}{3} & \text { khi } x=1 \end{array}\right.\) . Khẳng định nào sau đây đúng nhất?
A. Hàm số liên tục tại x =1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại x =1
D. Tất cả đều sai.
-
Câu 40:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x+1+\sqrt[3]{x-1}}{x} & \text { khi } x \neq 0 \\ 2 & \text { khi } x=0 \end{array}\right.\). Khẳng định nào sau đây đúng nhất?
A. Hàm số liên tục tại \(x_{0}=0.\)
B. Hàm số liên tục tại mọi điểm như gián đoạn tại \(x_{0}=0.\)
C. Hàm số không liên tục tại \(x_{0}=0\)
D. Tất cả đều sai
-
Câu 41:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x+\sqrt{x+2}}{x+1} & \text { khi } x>-1 \\ 2 x+3 & \text { khi } x \leq-1 \end{array}\right.\). Khẳng định nào sau đây đúng nhất?
A. Hàm số liên tục tại tại tại \(x_{0}=-1\)
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại\(x_{0}=-1\)
D. Tất cả đều sai.
-
Câu 42:
Chọn giá trị f (0) để các hàm số \(f(x)=\frac{\sqrt[3]{2 x+8}-2}{\sqrt{3 x+4}-2}\) liên tục tại điểm x=0.
A. 1
B. 2
C. \(\frac{2}{9}\)
D. \(\frac{1}{9}\)
-
Câu 43:
Chọn giá trị f (0) để các hàm số \(f(x)=\frac{\sqrt{2 x+1}-1}{x(x+1)}\) liên tục tại điểm x=0
A. 1
B. 2
C. 3
D. 4
-
Câu 44:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{x^{2}-3 x+2}{\sqrt{x-1}}+2 & \text { khi } x>1 \\ 3 x^{2}+x-1 & \text { khi } x \leq 1 \end{array}\right.\) . Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x = 1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại x =1
D. Tất cả đều sai.
-
Câu 45:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sqrt{x}-2}{x-4} & \text { khi } x \neq 4 \\ \frac{1}{4} & \text { khi } x=4 \end{array}\right.\). Khẳng định nào sau đây đúng?
A. Hàm số liên tục tại x = 4.
B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x = 4.
C. Hàm số không liên tục tại x = 4.
D. Tất cả đều sai.
-
Câu 46:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} (x+1)^{2} & , x>1 \\ x^{2}+3 & , x<1 \\ k^{2} & , x=1 \end{array}\right.\). Tìm k để \(f(x)\) gián đoạn tại x=1
A. \(k \neq\pm 2\)
B. \(k \neq 2\)
C. \(k \neq-2\)
D. \(k \neq\pm 1\)
-
Câu 47:
Cho hàm số \(f(x)=\left\{\begin{array}{ll} \frac{\sin 5 x}{5 x} & x \neq 0 \\ a+2 & x=0 \end{array}\right.\). Tìm a để \(f(x)\) liên tục tại x=0
A. 1
B. -1
C. 2
D. -2
-
Câu 48:
Giới hạn dãy số \(\left(u_{n}\right) \text { với } u_{n}=\frac{3 n-n^{4}}{4 n-5}\) là:
A. \(-\infty\)
B. \(+\infty\)
C. \(\frac{3}{4}\)
D. 0
-
Câu 49:
Giá trị của \(\lim \frac{-n^{2}+2 n+1}{\sqrt{3 n^{4}+2}}\) bằng:
A. \(-\frac{\sqrt{3}}{3}\)
B. \(-\frac{2}{3}\)
C. \(-\frac{1}{2}\)
D. \(\frac{1}{2}\)
-
Câu 50:
Kết quả đúng của \(\lim \left(5-\frac{n \cos 2 n}{n^{2}+1}\right)\) là
A. 4
B. 5
C. -4
D. \(\frac{1}{4}\)
