Trắc nghiệm Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán Lớp 12
-
Câu 1:
Tìm giá trị lớn nhất của hàm số y=3sinx−4sin3xy=3sinx−4sin3x trên đoạn [−π2;π2][−π2;π2].
A. -1
B. 1
C. 3
D. 7
-
Câu 2:
Tìm M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y=x+√2cosxy=x+√2cosx trên đoạn [0;π2][0;π2].
A. M=π4+1;m=√2M=π4+1;m=√2
B. M=π2;m=√2M=π2;m=√2
C. M=1;m=0M=1;m=0
D. M=√2;m=1M=√2;m=1
-
Câu 3:
Tìm giá trị lớn nhất của hàm số f(x)=x+cos2xf(x)=x+cos2x trên đoạn [0;π2][0;π2]
A. ππ
B. 00
C. π2π2
D. π4π4
-
Câu 4:
Cho hàm số y=|3cosx−4sinx+8|y=|3cosx−4sinx+8| với x∈[0;2π]x∈[0;2π]. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Khi đó tổng M + m bằng bao nhiêu?
A. 8√28√2
B. 7√37√3
C. 8√38√3
D. 16
-
Câu 5:
Giá trị nhỏ nhất của hàm số y=2cos3x−92cos2x+3cosx+12 là:
A. 1
B. -24
C. -12
D. -9
-
Câu 6:
Tìm giá trị lớn nhất của hàm số y=cos2x+4cosx+1
A. minRy=5
B. maxRy=6
C. minRy=7
D. minRy=8
-
Câu 7:
Tìm giá trị nhỏ nhất của hàm số y=2cos2x+4cosx
A. minRy=5
B. minRy=−2
C. minRy=7
D. minRy=8
-
Câu 8:
Giá trị nhỏ nhất của hàm số y=5sinx−cos2x là:
A. -6
B. -7
C. -4
D. 3
-
Câu 9:
Hàm số y=4√x2−2x+3+2x−x2 đạt giá trị lớn nhất tại hai giá trị x1,x2 . Tính x1.x2
A. 2
B. 1
C. 0
D. -1
-
Câu 10:
Cho hàm số y=5√3−x . Tìm giá trị nhỏ nhất của hàm số
A. 3
B. 2
C. 0
D. 5
-
Câu 11:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=√−x2+6x−5 trên đoạn [1;5] lần lượt là:
A. 2 và 0
B. 4 và 0
C. 3 và 0 .
D. 0 và -2
-
Câu 12:
Tìm giá trị lớn nhất của hàm số y=√x−1+√3−x trên đoạn [1;3].
A. max[1;3]y=2
B. max[1;3]y=√2
C. max[1;3]y=−√2
D. max[1;3]y=−2
-
Câu 13:
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)=2x−4√6−x trên đoạn [-3 ; 6]. Tổng M+m có giá trị là:
A. 18
B. -6
C. -12
D. -4
-
Câu 14:
Tìm giá trị nhỏ nhất của hàm số y=√5x2+4 trên đoạn [-3;1].
A. min[−3;1]y=3
B. min[−3;1]y=7
C. min[−3;1]y=2
D. min[−3;1]y=0
-
Câu 15:
Giá trị lớn nhất của hàm số y=√−x2+4x là:
A. 4
B. 0
C. -2
D. 2
-
Câu 16:
Giá trị nhỏ nhất của hàm số y=√6−x−√x+4 đạt tại x0,giá trị của x0 là:
A. x0=−√10
B. x0=−4
C. x0=6
D. x0=√10
-
Câu 17:
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y=−3+√4−x2 lần lượt là:
A. -3 và 0
B. -3 và -1
C. 0 và 2
D. -2 và 2
-
Câu 18:
Kết luận nào là đúng về giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=√x−x2?
A. Có giá trị lớn nhất và có giá trị nhỏ nhất
B. Có giá trị nhỏ nhất và không có giá trị lớn nhất
C. Có giá trị lớn nhất và không có giá trị nhỏ nhất
D. Không có giá trị lớn nhất và giá trị nhỏ nhất.
-
Câu 19:
Giá trị lớn nhất của hàm số f(x)=x2+3x−1x−2 trên đoạn [-2;0] là:
A. 2
B. 1
C. 4
D. 3
-
Câu 20:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=x2−2x+3x−1 trên đoạn [2;4] là:
A. min[2;4]f(x)=2;max[2;4]f(x)=113
B. min[2;4]f(x)=2√2;max[2;4]f(x)=3
C. min[2;4]f(x)=2;max[2;4]f(x)=3
D. min[2;4]f(x)=2√2;max[2;4]f(x)=113
-
Câu 21:
Hàm số y=x2−3xx+1 đạt giá trị lớn nhất trên đoạn [0;3] là:
A. 1
B. 3
C. 2
D. 0
-
Câu 22:
Giá trị lớn nhất của hàm số y=x(5−2x)2 trên [0; 3] là:
A. 0
B. 12527
C. 25027
D. 2503
-
Câu 23:
Giá trị lớn nhất của hàm số f(x)=−x2+4 là:
A. 0
B. 4
C. 2
D. Đáp án khác
-
Câu 24:
Cho hai số thực dương thỏa mãn 1≤x≤2;1≤y≤2 . Giá trị nhỏ nhất m của biểu thức P=x+2yx2+3y+5+y+2xy2+3x+5+14(x+y−1)
A. m=0
B. m=854
C. m=−10
D. m=78
-
Câu 25:
Cho a , b là các số thực dương thỏa mãn 2(a2+b2)+ab=(a+b)(ab+2). Giá trị nhỏ nhất m của biểu thức P=4(a3b3+b3a3)−9(a2b2+b2a2)
A. m=−10
B. m=854
C. m=−234
D. m=0
-
Câu 26:
Cho hai số thực x≠0,y≠0 thay đổi và thỏa mãn điều kiện (x+y)xy=x2+y2−xy . Giá trị lớn nhất M của biểu thức A=1x3+1y3 là:
A. M=0
B. M=1
C. M=2
D. M=16
-
Câu 27:
Cho các số thực x , y thoả mãn (x−4)2+(y−4)2+2xy≤32 Giá trị nhỏ nhất m của biểu thức A=x3+y3+3(xy−1)(x+y−2)
A. m=17−5√54
B. m=16
C. m=398
D. m=0
-
Câu 28:
Cho các số thực x , y thõa mãnx≥0,y≥0 và x+y=1
Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức S=(4x2+3y)(4y2+3x)+25xy là:A. M=252;m=19116
B. M=12;m=19116
C. M=252;m=12
D. M=252;m=0
-
Câu 29:
Giá trị lớn nhất, nhỏ nhất của hàm số y=2x2+3x+3x+1 trên đoạn [0;2] lần lượt là:
A. 173;3
B. 173;−5
C. 3;−5
D. −3;5
-
Câu 30:
Giá trị lớn nhất của hàm số y=ln2xx trên đoạn [1;e3] là :
A. 0
B. 9e3
C. 4e2
D. 4e
-
Câu 31:
Hàm số y=f(x)=x+1√x2+1 có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1;2] lần lượt bằng:
A. 3√5;0
B. √5;0
C. √2;0
D. √5;1√5
-
Câu 32:
Giá trị lớn nhất của hàm số y=x+√1+9x28x2+1 trên khoảng (0;+∞) là:
A. √32
B. 3√22
C. 3√24
D. −3√22
-
Câu 33:
Hàm số y=−2sin3x+3cos2x−6sinx+4 có giá trị lớn nhất bằng
A. -6
B. -7
C. 8
D. 9
-
Câu 34:
Hàm số y=2cos3x−72cos2x−3cosx+5 có giá trị nhỏ nhất bằng:
A. 32
B. 12
C. 52
D. 1
-
Câu 35:
Hàm số y=x+√18−x2 có giá trị lớn nhất bằng:
A. 5
B. -6
C. 6
D. -5
-
Câu 36:
Hàm số y=2sin2x+5cos2x−1 có giá trị nhỏ nhất bằng
A. 1
B. 2
C. 3
D. 4
-
Câu 37:
Giá trị lớn nhất của hàm số y=√x−2+√4−x là:
A. -2
B. 2
C. 3
D. -3
-
Câu 38:
Giá trị nhỏ nhất của hàm số y=(x+3)√−x2−2x+3 là:
A. 2
B. 1
C. 0
D. 3
-
Câu 39:
Giá trị lớn nhất của hàm số y=13x3−12x2−6x+3 trên đoạn [0;4] là:
A. −213
B. 2
C. 1
D. 3
-
Câu 40:
Cho hàm số y=sinx+1sin2x+sinx+1. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số đã cho. Chọn mệnh đề đúng
A. M=m+23
B. M=m+1
C. M=32m
D. M=m+32
-
Câu 41:
Cho hàm số y=2cos2x+|cosx|+1|cosx|+1. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số đã cho. Khi đó M+m bằng
A. -4
B. -6
C. -5
D. 3
-
Câu 42:
Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số y=sin4x+cos2x+2 là:
A. M=3;m=−114
B. M=114;m=−3
C. M=3;m=114
D. M=−114;m=−3
-
Câu 43:
Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số y=sin4x−4sin2x+5 là:
A. M=2 ; m=-5
B. M=5 ; m=2
C. M=5 ; m=-2
D. M=-2 ; m=-5
-
Câu 44:
Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số y=2cos2x+2sinx là
A. M=94;m=−4
B. M=4;m=0
C. M=0;m=−94
D. M=4;m=−94
-
Câu 45:
Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số:y=2sin2x+2sinx−1 là:
A. M=−1;m=−32
B. M=3;m=−1
C. M=3;m=−32
D. M=32;m=−3
-
Câu 46:
Cho một tấm nhôm hình vuông cạnh a. Người ta cắt ở 4 góc 4 hình vuông bằng nhau, rồi gập tấm nhôm lại để được một cái hộp không nắp. Tìm cạnh của hình vuông bị cắt sao cho thể tích của khối hộp là lớn nhất?
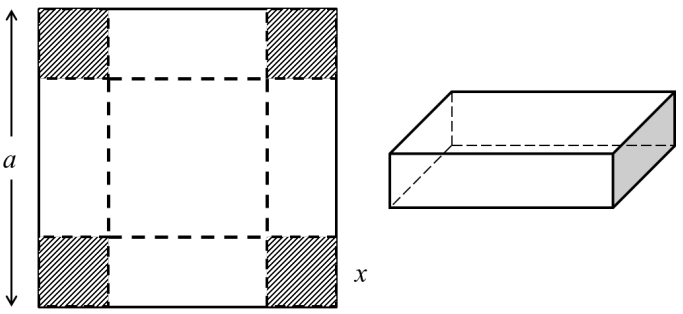
A. 5a6
B. a6
C. a12
D. a9
-
Câu 47:
Trong các hình trụ nội tiếp hình cầu bán kính R, hình trụ có thể tích lớn nhất bằng
A. ‘4πR3√3
B. 4πR33√3
C. πR33√3
D. 4πR33
-
Câu 48:
Một hộp không nắp được làm từ một mảnh các tông theo mẫu như hình vẽ. Hộp có đáy là một hình vuông cạnh x cm, chiều cao h cm và có thể tích 500 cm3. Giá trị của x để diện tích của mảnh các tông nhỏ nhất bằng
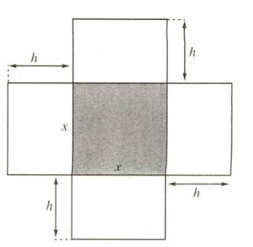
A. 100
B. 300
C. 10
D. 1000 .
-
Câu 49:
Cho ∆ABC đều cạnh a. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên BC, hai đỉnh P, Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định vị trí của điểm M sao cho hình chữ nhật có diện tích lớn nhất ?
A. BM=2a3
B. BM=3a4
C. BM=a3
D. BM=a4
-
Câu 50:
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f(t)=45t2−t3,t=0,1,2,…,25 Nếu coi f(t) là hàm số xác định trên đoạn [0;25] thì đạo hàm f’(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Xác định ngày mà tốc độ truyền bệnh là lớn nhất?
A. Ngày thứ 19.
B. Ngày thứ 5.
C. Ngày thứ 16.
D. Ngày thứ 15.














