Trắc nghiệm Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán Lớp 12

A. \(\min\limits _{x \in[0 ; \pi]} y=1\)

B. \(\min\limits _{x \in[0 ; \pi]} y=-1\)

C. \(\min\limits _{x \in[0 ; \pi]} y=0\)

D. \(\min\limits _{x \in[0 ; \pi]} y=-2\)

A. \(\max\limits _{x \in\left[-\frac{\pi}{2} ; 0\right]} f(x)=-1\)

B. \(\max\limits _{x \in\left[-\frac{\pi}{2} ; 0\right]} f(x)=1\)

C. \(\max\limits _{x \in\left[-\frac{\pi}{2} ; 0\right]} f(x)=0\)

D. \(\max\limits _{x \in\left[-\frac{\pi}{2} ; 0\right]} f(x)=2\)

A. \(\min \limits_{[2 ; 8]} y=y(2)=-\sqrt{6}\)

B. \(\min \limits_{[2 ; 8]} y=y(2)=\sqrt{6}\)

C. \(\min \limits_{[2 ; 8]} y=y(2)=2\sqrt{6}\)

D. \(\min \limits_{[2 ; 8]} y=y(2)=-2\sqrt{6}\)

A. \(\max\limits _{x \in[2 ; 4]} f(x)=4\)

B. \(\max\limits _{x \in[2 ; 4]} f(x)=2\)

C. \(\max\limits _{x \in[2 ; 4]} f(x)=6\)

D. \(\max\limits _{x \in[2 ; 4]} f(x)=8\)

A. \(\max\limits _{[0 ; 2]} y=\frac{1}{3} ; \min\limits _{[0 ; 2]} y=-5\)

B. \(\max\limits _{[0 ; 2]} y=5 ; \min\limits _{[0 ; 2]} y=-\frac{1}{3}\)

C. \(\max\limits _{[0 ; 2]} y=-\frac{1}{3} ; \min\limits _{[0 ; 2]} y=-5\)

D. \(\max\limits _{[0 ; 2]} y=5 ; \min\limits _{[0 ; 2]} y=\frac{1}{3}\)

A. \(\max\limits _{[-1 ; 5]} y=154\)

B. \(\max\limits _{[-1 ; 5]} y=-6\)

C. \(\max\limits _{[-1 ; 5]} y=47\)

D. \(\max\limits _{[-1 ; 5]} y=266\)

A. \(\min y=1\)

B. \(\min y=2\)

C. \(\min y=-2\)

D. \(\min y=-2\)

A. \(\max\limits _{\mathbb{R}} f(x)=1\)

B. \(\max\limits _{\mathbb{R}} f(x)=2\)

C. \(\max\limits _{\mathbb{R}} f(x)=3\)

D. \(\max\limits _{\mathbb{R}} f(x)=4\)

A. \(\min\limits _{(0 ;+\infty)} f(x)=\sqrt{2}\)

B. \(\min\limits _{(0 ;+\infty)} f(x)=2\)

C. \(\min\limits _{(0 ;+\infty)} f(x)=\sqrt{5}\)

D. \(\min\limits _{(0 ;+\infty)} f(x)=5\)

A. \(\max \limits_{(-\infty ; 1)} f(x)=\frac{1}{8}\)

B. \(\max \limits_{(-\infty ; 1)} f(x)=8\)

C. \(\max \limits_{(-\infty ; 1)} f(x)=5\)

D. \(\max \limits_{(-\infty ; 1)} f(x)=\frac{1}{5}\)

A. \(\max\limits _{\mathbb{R}} f(x)=\frac{47}{30}\)

B. \(\max\limits _{\mathbb{R}} f(x)=\frac{-47}{30}\)

C. \(\max\limits _{\mathbb{R}} f(x)=\frac{30}{47}\)

D. \(\max\limits _{\mathbb{R}} f(x)=\frac{37}{40}\)

A. \(\min\limits _{[0 ;+\infty)} f(x)=-1\)

B. \(\min\limits _{[0 ;+\infty)} f(x)=1\)

C. \(\min\limits _{[0 ;+\infty)} f(x)=0\)

D. Không tồn tại giá trị nhỏ nhất của hàm số.

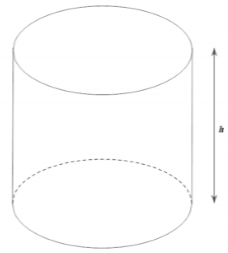
A. 10,5

B. 10,6

C. 10,7

D. 10,8

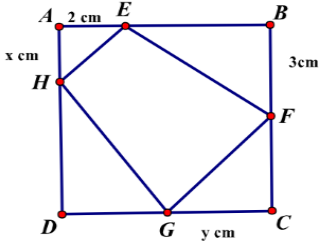
A. \(2 + \sqrt 3 \)

B. \(3 \sqrt 2 \)

C. \(2 \sqrt 2 \)

D. Tất cả sai 

A. \(m\le 2\)

B. \(m\le 1\)

C. \(m > 2\)

D. Đáp án khác 

A. 0 < m < 1

B. m < 0

C. m > 0

D. - 1 < m < 0

A. m = 1

B. m = 3

C. m = 5

D. m = - 1

A. (0;1)

B. \(\left( {\frac{1}{2};1} \right)\)0

C. (2;3)

D. (0;2)

A. 1 < m < 3

B. \( m\in \left( {1;3\sqrt 5 \; - \;4} \right)\)

C. \(m \in \;\left( {1;\sqrt 5 } \right)\)

D. \(1 < m \le 4\)

A. m = 0

B. m = 2

C. m = 4

D. m = 5

A. - 4

B. 2

C. 0

D. - 2

A. m = 1

B. m = - 2

C. m = - 1

D. m = - 1 hoặc m = 2

A. \(f(a)\)

B. \(f\left( {\sqrt {ab} } \right)\)

C. \(f(b\)

D. \(f\left( {\frac{{a + b}}{2}} \right)\)

A. 6

B. 8

C. 7

D. 9

A. 20 và 18

B. 20 và 15.

C. 16 và 15

D. 16  và 13.

A. 4

B. 3

C. 1

D. 2

A. 4

B. 5

C. 6

D. 3

A. 4

B. 6

C. 5

D. 8

A. 3

B. 4

C. 1

D. 2

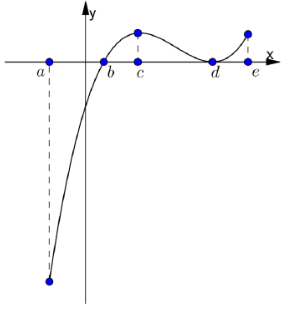
A. \(\left\{ {\begin{array}{*{20}{l}} {\mathop {max}\limits_{\left[ {a,e} \right]} \;f\left( x \right) = f\left( c \right)}\\ {\mathop {min}\limits_{\left[ {a,e} \right]} \;f\left( x \right) = f\left( a \right)} \end{array}} \right.\)

B. \(\left\{ {\begin{array}{*{20}{l}} {\mathop {max}\limits_{\left[ {a,e} \right]} \;f\left( x \right) = f\left( a \right)}\\ {\mathop {min}\limits_{\left[ {a,e} \right]} \;f\left( x \right) = f\left( b \right)} \end{array}} \right.\)

C. \(\left\{ {\begin{array}{*{20}{l}} {\mathop {max}\limits_{\left[ {a,e} \right]} \;f\left( x \right) = f\left( e \right)}\\ {\mathop {min}\limits_{\left[ {a,e} \right]} \;f\left( x \right) = f\left( b \right)} \end{array}} \right.\)

D. \(\left\{ {\begin{array}{*{20}{l}} {\mathop {max}\limits_{\left[ {a,e} \right]} \;f\left( x \right) = f\left( d \right)}\\ {\mathop {min}\limits_{\left[ {a,e} \right]} \;f\left( x \right) = f\left( b \right)} \end{array}} \right.\)

A. m < - 1

B. \(m \le  - \frac{4}{7}\)

C. \(m \ge  - \frac{4}{7}\)

D. m > - 1

A. 1

B. 2

C. \(\frac{3}{2}\)

D. 0

A. \(2\sqrt 2  + 4;\;2.\)

B. \(2\sqrt 2  -2;\;2.\)

C. \(2\sqrt 2;\;2.\)

D. \(4;2\)

A. \(2\sqrt 2  - 2;\;2.\)

B. \(2\sqrt 2  + 2;\;2.\)

C. \(2\sqrt 2  ;\;2.\)

D. \(0;\;2.\)

A. \(\frac{{28}}{{27}}\).

B. 4

C. \(\frac{{82}}{{27}}\).

D. 2

A. 5

B. 6

C. 4

D. Tất cả sai

A. Có giá trị lớn nhất và có giá trị nhỏ nhất

B. Có giá trị nhỏ nhất và không có giá trị lớn nhất

C. Có giá trị lớn nhất và không có giá trị nhỏ nhất

D. Không có giá trị lớn nhất và giá trị nhỏ nhất

A. - 3 và 0.

B. - 3 và - 1

C. 0 và 2

D. - 2 và 2.

A. min_{[-3; 1]}y = 3

B. min_{[-3; 1]}y = 7

C. min_{[-3; 1]}y = 2

D. min_{[-3; 1]}y = 0

A. - 1

B. 0

C. 2

D. 1

A.  min_[0;3]y = 0

B.  min_[0;3]y = \( - \frac{3}{7}\)

C.  min_[0;3]y = - 4

D.  min_[0;3]y = - 1

A. \( - \frac{{338}}{{27}}\)

B. \( - \frac{{446}}{{27}}\)

C. \(- 10\)

D. \( - \frac{{14}}{{27}}\)

A. M = 40; m = - 41

B. M = 40; m = - 8

C. M = - 41; m = 40

D. M = 15; m = - 8

A. \( - \frac{1}{3}\)

B. - 5

C. 5

D. \(  \frac{1}{3}\)

A. Có giá trị nhỏ nhất tại x = -1 và giá trị lớn nhất tại x = 1

B. Có giá trị nhỏ nhất tại x = 1 và giá trị lớn nhất tại x = - 1

C. Có giá trị nhỏ nhất tại x = - 1 và không có giá trị lớn nhất

D. Không có giá trị nhỏ nhất và có giá trị lớn nhất tại x = 1

A. min_[2 ;4] y = 6

B. min_[2 ;4] y = - 2

C. min_[2 ;4] y = - 3

D. min_[2 ;4] y = 19/3

A. 1

B. 3

C. 2

D. 0

A. d = 3

B. d = 4

C. d = 5

D. d = 2

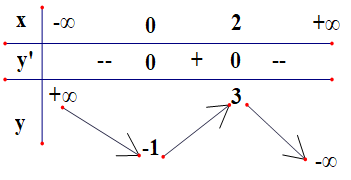
A. Hàm số có 2 cực trị

B. Hàm số có giá trị cực đại bằng 3

C. Hàm số có giá trị lớn nhất bằng 3, giá trị nhỏ nhất bằng -1

D. Hàm số đạt cực tiểu tại x = 0

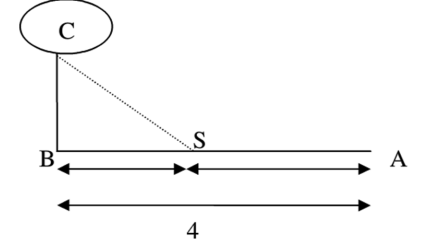
A. \(\frac{15}{4} \mathrm{km}\)

B. \(\frac{13}{4} \mathrm{km}\)

C. \(\frac{10}{4} \mathrm{km}\)

D. \(\frac{19}{4} \mathrm{km}\)