Cho hàm số \(y = \left| {{x^4} - 4{x^3} + 4{x^2} + a} \right|\). Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M ≤ 2m?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai+ Xét hàm số y = x4 - 4x3+ 4x2+ a trên đoạn [ 0; 2].
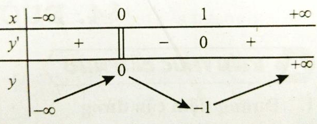
Ta có đạo hàm y’ = 4x3-12x2+ 8x
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 1\\
x = 2
\end{array} \right.\)
Khi đó; y( 0) = y( 2) = a; y( 1) = a+ 1
+ Nếu a ≥ 0 thì M = a+ 1,m = a.
Để M ≤ 2m khi a ≥ 1, suy ra {1;2;3} thỏa mãn
+ Nếu a ≤ - 1 thì \(M = \left| a \right| = - a,\;m = \left| {a + 1} \right| = - a - 1.\)
Để M ≤ 2m thì a ≤ - 2, suy ra a {−2;−3}
Vậy có 5 giá trị nguyên của a thỏa mãn yêu cầu.
Câu hỏi liên quan
-
Cho hàm số y=f(x) xác định và liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y=f(x) trên đoạn [-2;2]?
-
Tìm giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} – 3{x^2} – 9x + 10\) trên \(\left[ { – 2;\;2} \right]\).
-
Tìm giá trị nhỏ nhất của hàm số \(y=x+\frac{9}{x}\) trên đoạn \([2 ; 4] .\)
-
Tìm giá trị nhỏ nhất của hàm số \(y=2 \sin ^{2} x+5 \cos ^{2} x-1\)
-
Gia trị lớn nhất của hàm số \(y=\frac{x^2+3x+3}{x+1}\) trên đoạn \(\left[ { - \frac{1}{2};1} \right]\)
-
Cho hàm số \(y = 5\sqrt {3 - x} \). Tìm giá trị nhỏ nhất của hàm số.
-
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Đồ thị của hàm số \(y = f’\left( x \right)\) như hình bên. Đặt \(g\left( x \right) = 2f\left( x \right) – {\left( {x + 1} \right)^2}\). Mệnh đề nào dưới đây đúng?
.jpg.png)
-
Cho hàm số \(y = {x^3} + 3m{x^2} + 3\left( {2m – 1} \right)x + 1\) (với m là tham số). Tìm tất cả các giá trị của tham số m để trên đoạn \(\left[ { – 2;0} \right]\) hàm số trên đạt giá trị lớn nhất bằng 6.
-
Giá trị nhỏ nhất của hàm số \(y=\frac{x-1}{x+1}\) trên đoạn [0;3] là:
-
\(\text{Tìm giá trị lớn nhất của hàm số }y = f\left( x \right) = \frac{{4x - 7}}{x}\text{ trên đoạn } \left[ {1;3} \right]\)
-
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{ - x + 3}}{{2x + 5}}\text{ trên đoạn } \left[ { - 1;2} \right]\)
-
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f’\left( x \right)\) có bảng biến thiên như sau:
.png)
Bất phương trình \(f\left( x \right) < {x^3} + m\) đúng với mọi \(x \in \left( { – 1\,;\,1} \right)\) khi và chỉ khi
-
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = - 3 + \sqrt {4 - {x^2}} \) lần lượt là
-
Giá trị nhỏ nhất của hàm số \(y=x+\frac{9}{x}\) trên đoạn [2;4] là:
-
Tìm tập giá trị T của hàm số \(y = x + \sqrt {4 – {x^2}} .\).
-
Tìm GTLN và GTNN của các hàm số sau \(y=\frac{2 \sin x-1}{\sin x+2}\)
-
Cho hàm số \(y=2 x^{3}-3 x^{2}-m\) . Trên \([-1 ; 1]\) hàm số có giá trị nhỏ nhất là -1 . Tính m
-
Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số:\(y=2 \sin ^{2} x+2 \sin x-1\) là:
-
Giá trị lớn nhất của hàm số \(y=\sqrt{x+4}+\sqrt{4-x}-4 \sqrt{(x+4)(4-x)}+5\) bằng
-
Giá trị lớn nhất của hàm số \(f(x)=\frac{9}{x}+x\) trên khoảng \((-\infty ; 0)\)bằng
