ADMICRO
GTLN của hàm số \(y = \frac{{x + 1}}{{{x^2} + 1}}\) trên khoảng (0; 4) đạt được
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
ZUNIA12
Lời giải:
Báo saiXét
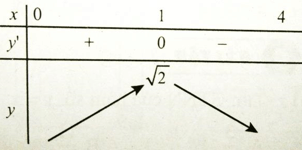
\(y' = \frac{{\sqrt {{x^2} + 1} - \left( {x + 1} \right)\frac{x}{{\sqrt {{x^2} + 1} }}}}{{{x^2} + 1}} = \frac{{1 - x}}{{{{\left( {\sqrt {{x^2} + 1} } \right)}^3}}}\)
Ta có: \(y' = 0 \Rightarrow x = 1\)
Vậy hàm số có GTLN bằng \(\sqrt 2 \) khi x = 1 .
ZUNIA9
AANETWORK



.PNG)
.png)











