Cho \(x^{2}-x y+y^{2}=2 \text { . }\)Giá trị nhỏ nhất của \(P=x^{2}+x y+y^{2} b\) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\text { Xét } \frac{P}{2}=\frac{x^{2}+x y+y^{2}}{2}=\frac{x^{2}+x y+y^{2}}{x^{2}-x y+y^{2}}\)
+\(\text { Nếu } y=0 \text { thì } x^{2}=2 \text { . Do đó } P=x^{2}=2 \text { suy ra } \min P=2\)
+\(\text { Nếu } y \neq 0 \text { ta chia tử mẫu cho } y^{2} \text { ta được: } \frac{P}{2}=\frac{x^{2}+x y+y^{2}}{x^{2}-x y+y^{2}}=\frac{1+\left(\frac{x}{y}\right)+\left(\frac{x}{y}\right)^{2}}{1-\left(\frac{x}{y}\right)+\left(\frac{x}{y}\right)^{2}}\)
\(\text { Đặt } t=\frac{x}{y}, \text { khi đó } \frac{P}{2}=\frac{1+t+t^{2}}{1-t+t^{2}} \text { . Xét } f(t)=\frac{1+t+t^{2}}{1-t+t^{2}} \Rightarrow f^{\prime}(t)=\frac{-2 t^{2}+2}{\left(1-t+t^{2}\right)^{2}} ; f^{\prime}(t)=0 \Leftrightarrow\left[\begin{array}{l} t=1 \\ t=-1 \end{array}\right.\)
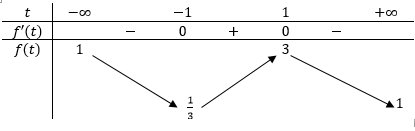
Bảng biến thiên:
\(\text { Khi đó } \min \frac{P}{2}=\frac{1}{3} \text { do đó } \min P=\frac{2}{3} \text { . }\)



.png)











