Trắc nghiệm Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán Lớp 12
-
Câu 1:
Cho một tờ giấy hình chữ nhật với chiều dài 12 cm và chiều rộng 8 cm. Gấp góc bên phải của tờ giấy sao cho góc ở đỉnh của nó chạm với đáy như hình vẽ. Khi độ dài nếp gấp là nhỏ nhất thì giá trị nhỏ nhất đó là bao nhiêu.
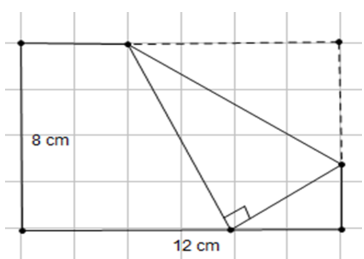
A. 6√15+6√3
B. 6√15−6√3
C. 8√2
D. 6√3
-
Câu 2:
Một công ty muốn làm đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn đảo. Hòn đảo cách bờ biển 6 km . Giá để xây đường ống trên bờ là 50000 USD mỗi km , và 130000 USD mỗi km để xây dưới nước. B' là điểm trên bờ biển sao cho BB' vuông góc với bờ biển. Khoảng cách từ A đến B' là 9 km . Vị trí C trên đoạn AB' sao cho khi nối ống theo ACB thì số tiền ít nhất. Khi đó C cách A một đoạn bằng bao nhiêu ?
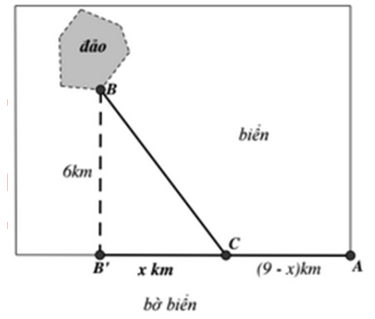
A. 6,5km
B. 6km
C. 0km
D. 9km
-
Câu 3:
Một chất điểm chuyển động theo phương trình S=−2t3+18t2+2t+1 trong đó t tính bằng giây (s) và S tính bằng mét (m). Thời gian vận tốc chất điểm đạt giá trị lớn nhất là
A. t=5s
B. t=6s
C. t=3s
D. t=1s
-
Câu 4:
Khi xây nhà, chủ nhà cần làm một bồn nước bằng gạch và xi măng có dạng hình hộp đứng đáy là hình chữ nhật có chiều rộng là x(m), chiều dài gấp 2 lần chiều rộng và không nắp, có chiều cao là h(m) có thể tích là 43m3 Tìm chiều rộng của đáy hình chữ nhật để chi phí xây dựng là thấp nhất.
A. x=1,5(m)
B. x=2(m)
C. x=1(m)
D. x=2,5(m)
-
Câu 5:
Một trang chữ của một quyển sách tham khảo Văn học cần diện tíc 384 cm2 . Biết rằng trang giấy được canh lề trái là 2 cm , lề phải là 2 cm , lề trên 3 cm và lề dưới là 3 cm . Tìm chiều dài và chiều rộng của trang sách để trang sách có diện tích nhỏ nhất
A. Chiều dài: 32 cm và chiều rộng: 12 cm .
B. Chiều dài: 24 cm và chiều rộng: 16 cm .
C. Chiều dài: 40 cm và chiều rộng: 20 cm .
D. Chiều dài: 30 cm và chiều rộng: 20 cm
-
Câu 6:
Cho hàm số y=5√3−x. Tìm giá trị nhỏ nhất của hàm số.
A. 3
B. 5
C. 0
D. 1
-
Câu 7:
Giá trị nhỏ nhất của hàm số y=√6−x−√x+4 đạt tại x0, tìm x0?
A. x0 = √10
B. x0 = - 4
C. x0 = 6
D. x0 = −√10
-
Câu 8:
Hàm số y=4√x2−2x+3+2x−x2 đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là
A. 2
B. 1
C. 0
D. - 1
-
Câu 9:
Hàm số y=√4−x−√x+6 đạt giá trị nhỏ nhất tại x = x0. Tìm x0
A. x0 = -6
B. x0 = - 1
C. x0 = 0
D. x0 = 4
-
Câu 10:
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)=2x−4√6−x trên đoạn [-3;6]. Tổng M + m có giá trị là
A. 18
B. - 6
C. - 12
D. - 4
-
Câu 11:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=√−x2+6x−5 trên đoạn [1;5] lần lượt là
A. 2 và 0
B. 4 và 0
C. 3 và 0
D. 0 và -2
-
Câu 12:
Giá trị lớn nhất của hàm số y=√−x2+4x là:
A. 4
B. 0
C. - 2
D. 2
-
Câu 13:
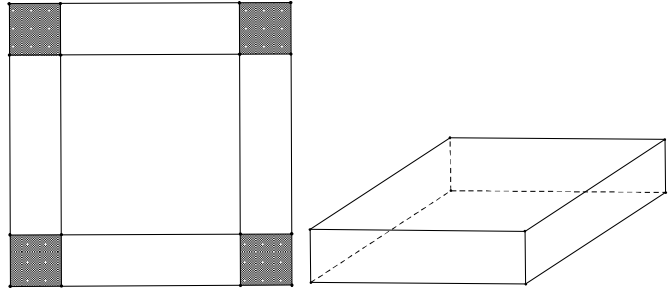
Cho hình vẽ
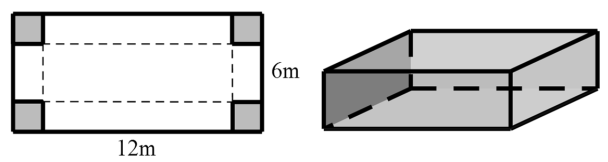
Bạn An có một tấm nhôm hình chữ nhật có chiều dài 12(m), chiều rộng 6(m). Bạn nhờ bác thợ hàn cắt ở bốn góc bốn hình vuông bằng nhau và gập tấm nhôm lại (như hình trên) để được một cái hộp không nắp dùng để đựng nước. Hỏi bác thợ hàn phải cắt cạnh hình vuông bằng bao nhiêu sao cho khối hộp chứa được nhiều nước nhất ?
A. 24√3(m)
B. 3−√3(m)
C. 3+√3(m)
D. 24−√3(m)
-
Câu 14:
Cho một tấm nhôm hình vuông cạnh 24cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông cạnh bằng nhau, mỗi hình vuông có cạnh bằng x (cm) rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất
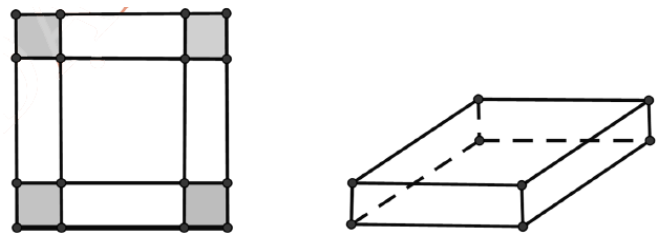
A. x=6
B. x=4
C. x=2
D. x=8
-
Câu 15:
Cho một tấm nhôm hình vuông cạnh 18 cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x cm , rồi gấp tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
A. x=2
B. x=4
C. x=6
D. x=3
-
Câu 16:
Hình chữ nhật có chu vi không đổi là 8 m. Diện tích lớn nhất của hình chữ nhật đó là:
A. 4m2
B. 16m2
C. 8m2
D. 2m2
-
Câu 17:
Cho x, y là hai số không âm thỏa mãn x+y=2 . Tìm giá trị nhỏ nhất của biểu thức P=13x3+x2+y2−x+1
A. minP=5
B. minP=73
C. minP=173
D. minP=1153
-
Câu 18:
Giá trị lớn nhất của hàm số f(x)=9x+x trên khoảng (−∞;0)bằng
A. 3
B. -6
C. -9
D. -3
-
Câu 19:
Giá trị nhỏ nhất của hàm số y=sin3x−cos2x+sinx+23 trên khoảng (−π2;π2) bằng:
A. 2327
B. 6
C. -1
D. 1
-
Câu 20:
Tìm giá trị nhỏ nhất của hàm số y=2√3−x trên nửa khoảng [−4;−2)
A. ymin=0
B. ymin=−6
C. ymin=−3
D. ymin=2
-
Câu 21:
Tìm giá trị lớn nhất của hàm số y=x2−3x−2 trên khoảng (−∞;2)
A. max(−∞;2)y=4
B. max(−∞;2)y=3
C. max(−∞;2)y=1
D. max(−∞;2)y=2
-
Câu 22:
Hàm số y=1x2+1 có bảng biến thiên như hình vẽ. Xét trên tập xác định của hàm số. Hãy chọn khẳng định đúng ?
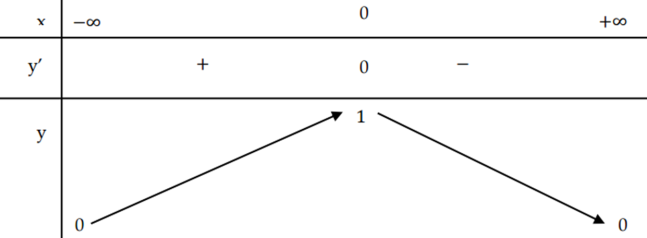
A. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
B. Hàm số có giá trị lớn nhất bằng 0.
C. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
D. Hàm số có giá trị lớn nhất bằng 1.
-
Câu 23:
Tìm giá trị nhỏ nhất của hàm số y=x+4x trên khoảng (0;+∞)
A. 4
B. 2
C. -2
D. -4
-
Câu 24:
Trên khoảng (0;+∞) thì hàm số y=−x3+3x+1
A. Có giá trị nhỏ nhất là miny=3
B. Có giá trị lớn nhất là maxy=−1
C. Có giá trị nhỏ nhất là miny=−1
D. Có giá trị lớn nhất là maxy=3
-
Câu 25:
Biết rằng giá trị lớn nhất của hàm sốy=ln2xx trên đoạn [1;e3]là M=men trong đó m, n là các số tự nhiên. Tính S=m2+2n3
A. S=135
B. S=24
C. S=22
D. S=32
-
Câu 26:
Tìm GTLN và GTNN của hàm số f(x)=(x2−2)⋅e2x trên đoạn [-1 ; 2].
A. 2e4vè−e2
B. 2e4và−1e2
C. 4e4và−e2
D. 4e4và−1e2
-
Câu 27:
Tìm GTLN và GTNN của hàm số f(x)=x+9x trên đoạn [1;4] là:
A. max[1;4](x)=10,min[1;4]f(x)=6
B. max[1;4](x)=9,min[1;4]f(x)=−6
C. max[1;4](x)=9,min[1;4]f(x)=6
D. max[1;4](x)=10,min[1;4]f(x)=−6
-
Câu 28:
Tính giá trị lớn nhất của hàm số y=x−lnx trên [12;e]
A. maxx∈[12,e]y=e−1.
B. maxx∈[12,e]y=1
C. maxx∈[12,e]y=e
D. maxx∈[12;e]y=12+ln2
-
Câu 29:
Tìm giá trị nhỏ nhất của hàm số y=2x+ln(1−2x) trên [−1;0]
A. minx∈[−1;0]=−2+ln3
B. minx∈[−1,0]=0
C. minx∈[−1,0]=−1
D. minx∈[−1;0]=2+ln3
-
Câu 30:
Giá trị nhỏ nhất của hàm số f(x)=x(2−lnx) trên [2;3] là
A. 1
B. 4−2ln2
C. e
D. −2+2ln2
-
Câu 31:
Giá trị lớn nhất của hàm số f(x)=lnxx trên đoạn [1;3] là:
A. 1e
B. e
C. ln33
D. 24,2
-
Câu 32:
Tìm GTLN và GTNN của các hàm số sau y=2sinx+cosx+1sinx−2cosx+3
A. {maxy=1miny=−12
B. {maxy=2miny=12
C. {maxy=2miny=1
D. {maxy=2miny=−12
-
Câu 33:
Tìm GTLN và GTNN của các hàm số sau y=2sinx−1sinx+2
A. maxy=13
B. maxy=−13
C. miny=−3
D. miny=12
-
Câu 34:
Một nhà máy sản xuất được 60000 sản phẩm trong một ngày và tổng chi phí sản xuất x sản phẩm được cho bởi:
P(x)=250000+0,08x+200000000x
Hỏi nhà máy nên sản xuất bao nhiêu sản phẩm mỗi ngày để chi phí sản xuất là nhỏ nhất?
A. 30000
B. 40000
C. 50000
D. 60000
-
Câu 35:
Khu chung cư Royal City có 250 căn hộ cho thuê. Nếu người ta cho thuê x căn hộ thì lợi nhuận hàng tháng, tính theo triệu đồng, được cho bởi: P(x)=−8x2+3200x−−80000.. Hỏi lợi nhuận tối đa họ có thể đạt được là bao nhiêu?
A. 150000
B. 220000
C. 292000
D. 250000
-
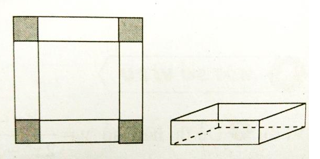
Câu 36:
Cho tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ bên để được một cái hộp không nắp. Với giá trị nào của x thì hộp nhận được có thể tích lớn nhất?
A. 6
B. 4
C. 3
D. 2
-
Câu 37:
Xét hàm số y=x2x−1
Trong các khẳng định sau, khẳng định nào là đúng?
A. Hàm số có giá trị lớn nhất bằng 4.
B. Hàm số có giá trị cực đại bằng 4.
C. Hàm số có giá trị lớn nhất bằng 0.
D. Hàm số có giá trị cực đại bằng 0.
-
Câu 38:
Cho hàm số y = f(x) xác định và liên tục trên R và có bảng biến thiên. Khẳng định nào sau đây là khẳng định đúng?
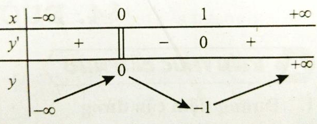
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1.
D. Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 1.
-
Câu 39:
GTLN của hàm số y = 2sinx + cos2x trên đoạn [0; π] là
A. 1
B. 32
C. 2
D. 74
-
Câu 40:
GTNN của hàm số y=x+2+1(x−1) trên khoảng (1; +∞) là:
A. Không tồn tại
B. 5
C. 1
D. 2
-
Câu 41:
GTNN của hàm số y=x(x+2) trên nửa khoảng (-2;4] là
A. 0
B. 1
C. 3
D. Không tồn tại
-
Câu 42:
GTLN của hàm số y=x4−8x2+16 trên đoạn [-1;3] là
A. 0
B. 15
C. 25
D. 30
-
Câu 43:
GTNN của hàm số y=x3+3x2−9x+1 trên đoạn [-4;4] là
A. - 4
B. 1
C. 4
D. - 1
-
Câu 44:
Tìm GTNN của hàm số y=x2−3x+5?
A. 32.
B. 114
C. 3
D. 5
-
Câu 45:
Một hành lang giữa hai tòa tháp có hình dạng một hình lăng trụ đứng. Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20m, rộng 5m. Với độ dài xấp xỉ nào của BC thì thể tích hành lang này lớn nhất
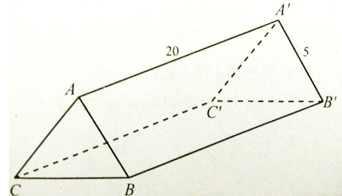
A. 6m
B. 7m
C. 8m
D. 9m
-
Câu 46:
Tìm GTLN của hàm số y=x−√x2+1 ?
A. 0
B. 1
C. Không tồn tại
D. Không có đáp án
-
Câu 47:
GTLN của hàm số y=x+1x2+1 trên khoảng (0; 4) đạt được
A. x = 1
B. x = - 1
C. x=√2
D. Không tồn tại
-
Câu 48:
GTLN của hàm số y=−x2+4x+7 đạt được khi x bằng:
A. 11
B. 4
C. 7
D. 2
-
Câu 49:
Một công ti quản lí chuẩn bị xây dựng một khu chung cư mới. Họ tính toán nếu tòa nhà có x căn hộ thì chi phí bảo trì của tòa nhà là: C(x)=4000−14x+0,04x2.. Khu đất của họ có thể xây được tòa nhà chứa tối đa 300 căn hộ. Hỏi họ nên xây dựng tòa nhà có bao nhiêu căn hộ để chi phí bảo trì của tòa nhà là nhỏ nhất?
A. 150
B. 175
C. 300
D. 225
-
Câu 50:
Giá trị lớn nhất của hàm số y={−x2+3,−2≤x≤03−x,0<x≤3x−3,3<x≤7 có đồ thị như hình bên là

A. 3
B. 7
C. - 1
D. 4














