Trắc nghiệm Đường tiệm cận Toán Lớp 12

Câu 1:

Đồ thị hàm số $y = \frac{{\sqrt {{x^2} + 3} - 2}}{{{x^2} - 3x + 2}}$ có bao nhiêu đường tiệm cận đứng?

Câu 2:

Tìm tất cả các giá trị thực của tham số mm để đồ thị hàm số $y = \frac{{x - 1}}{{x - m}}$ có tiệm cận đứng.

Câu 3:

Hàm số $y = \frac{{2x - 1}}{{x - 1}}{\mkern 1mu} {\mkern 1mu} \left( H \right)$. Gọi M là một điểm bất kì thuộc (H). Tiếp tuyến với (H) tại M tạo với hai đường tiệm cận một tam giác có diện tích bằng:

Câu 4:

Đồ thị hàm số $y = \frac{{{x^2} - 3x + 4}}{{x - 2}}$ có tiệm cận đứng là đường thẳng

Câu 5:

Cho hàm số $y = \frac{{x - 1}}{{x - 2}}$ có đồ thị (C). Có bao nhiêu điểm M ∈ (C) sao cho tổng khoảng cách từ M đến hai đường tiệm cận bằng 2?

Câu 6:

Cho hàm số $y = \frac{{m{x^2} - 2x + 1}}{{x - 2}}{\mkern 1mu} {\mkern 1mu} \left( C \right)$. Với giá trị nào của m thì đồ thị hàm số (C) không có tiệm cận xiên?

Câu 7:

Tìm các tiệm cận đứng và ngang của đồ thị mỗi hàm số sau: $y = \frac{{{x^2} - x - 2}}{{{{(x - 1)}^2}}}$

Câu 8:

Số tiệm cận của đồ thị hàm số  $y = \frac{{3x + 1}}{{3 - 2x}}$

Câu 9:

Tiệm cận đứng của đồ thị hàm số $y = \frac{{2{x^2} - x + 2}}{{{x^2} - 5}}$

Câu 10:

Tiệm cận đứng và ngang của đồ thị hàm số $y = - \frac{3}{{x - 2}}$

Câu 11:

Tiệm cận ngang của đồ thị hàm số $y = \frac{{{x^2} - 12x + 27}}{{{x^2} - 4x + 5}}$

Câu 12:

Cho hàm số $y = \frac{{3x - 1}}{{x + 4}}$. Gọi II là giao điểm của hai đường tiệm cận. Tính OI

Câu 13:

Tọa độ giao điểm hai đường tiệm cận của đồ thị hàm số $y=\frac{x-2}{x+1}$ là

Câu 14:

Tiệm cận ngang của đồ thị hàm số $y=\frac{x-20221}{x+2020}$ là

Câu 15:

Cho hàm số $y = \frac{{2{x^2} - 3x + m}}{{x - m}}$ . Để đồ thị hàm số không có tiệm cận đứng thì các giá trị của tham số m là:

Câu 16:

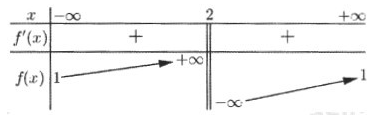
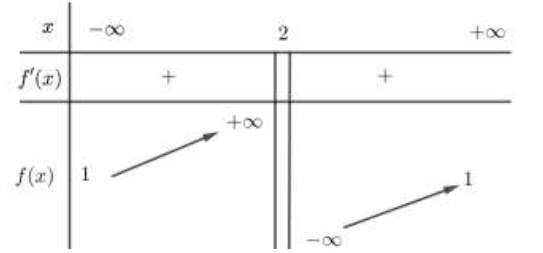
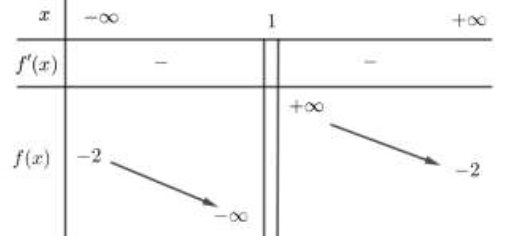
Cho hàm số $f\left( x \right) = \frac{{ax + 1}}{{bx + c}}$ (a,b,c thuộc R) có bảng biến thiên như sau: 

Trong các số (a,b ) và (c ) có bao nhiêu số dương ?

Câu 17:

Số đường tiệm cận của đồ thị hàm số ${y = \frac{{x - 2}}{{\sqrt {{x^2} - 4} }}}$

Câu 18:

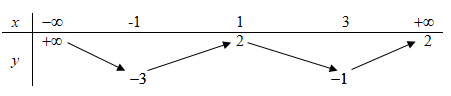
Cho hàm số y = f( x ) có bảng biến thiên như sau:

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số$y = \frac{1}{{f\left( x \right) - 1}}$

Câu 19:

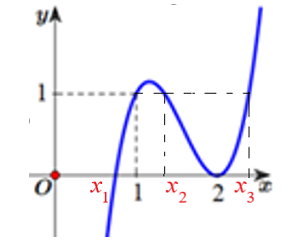
Cho hàm số $f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số $g(x) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}}$ có bao nhiêu tiệm cận đứng?

Câu 20:

Cho hàm số $y = \frac{{a{x^2} + 3ax + 2a + 1}}{{x + 2}}$. Chọn kết luận đúng:

Câu 21:

Số tiệm cận của đồ thị hàm số $y=\frac{\sqrt{x^{2}-3}}{x-1}$ là?

Câu 22:

Tìm điểm M thuộc đồ thị hàm số $y=\frac{2 x+1}{x-1}$ sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến trục hoành?

Câu 23:

Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y=\frac{x^{2}-m x-2 m^{2}}{x-2}$ có tiệm cận đứng 

Câu 24:

Số tiệm cận của đồ thị hàm số $y=\left\{\begin{array}{l} \frac{\sqrt{x^{2}+1}}{x} \text { nếu } x \geq 1 \\ \frac{2 x}{x-1} \text { nếu } x<1 \end{array} .\right.$

Câu 25:

Số đường tiệm cận của đồ thị hàm số $y=\frac{\sqrt{4-x^{2}}}{x^{2}-3 x-4}$ là:
 

Câu 26:

Đồ thị hàm số $y=\frac{\sqrt{x^{2}-x+1}+m x}{x-1}$ có đường tiệm cận đứng khi 

Câu 27:

Số tiệm cận của hàm số $y=\frac{\sqrt{x^{2}+1}+\sqrt[3]{x^{3}+3 x^{2}+1}}{x-1}$ là?

Câu 28:

Số tiệm cận của hàm số $y=\frac{\sqrt{x^{2}+1}-x}{\sqrt{x^{2}-9}-4}$ là:

Câu 29:

Với giá trị nào của m thì đồ thị $(\mathrm{C}): y=\frac{m x-1}{2 x+m}$ có tiệm cận đứng đi qua điểm $M(-1 ; \sqrt{2}) ?$

Câu 30:

Tìm tất cả các đường tiệm cận của đồ thị hàm số $y=\frac{x+3}{\sqrt{x^{2}+1}}$

Câu 31:

Số đường tiệm cận của đồ thị hàm số $y=\frac{2 x-1}{x^{2}-3 x+2}$ là:

Câu 32:

Đồ thị hàm số $y=\frac{2 x-7}{x+2}$ có bao nhiêu đường tiệm cận? 

Câu 33:

Đồ thị hàm số $y=\frac{3 x-1}{3 x+2}$ có đường tiệm cận ngang là

Câu 34:

Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang $y=\frac{1-3 x^{2}}{x^{2}-6 x+9}$ lần lượt là 

Câu 35:

Đồ thị hàm số $y=\frac{2 x-3}{x^{2}-3 x+2}$ có các đường tiệm cận đứng và tiệm cận ngang lần lượt là: 

Câu 36:

Đồ thị hàm số $y=\frac{1-3 x}{x+2}$ có các đường tiệm cận đứng và tiệm cận ngang lần lượt là: 

Câu 37:

Đồ thị hàm số $y=\frac{2 x-11}{x-1}$ có các đường tiệm cận đứng và tiệm cận ngang lần lượt là: 

Câu 38:

Cho hàm số$y=\frac{2 x-3}{x-2}(C)$. Gọi d là tiếp tuyến bất kì của (C), d cắt hai đường tiệm cận của đồ thị (C) lần lượt tại A, B. Khi đó khoảng cách giữa A và B ngắn nhất bằng 

Câu 39:

Cho hàm số $y=\frac{2 x-3}{x-2}(C)$. Gọi d là khoảng cách từ giao điểm của 2 tiệm cận của (C) đến một tiếp tuyến bất kỳ của đồ thị (C). Giá trị lớn nhất của d là 

Câu 40:

Cho hàm số $y=\frac{2 x-3}{x-2}(C)$. Gọi M là điểm bất kỳ trên (C), d là tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C). Giá trị nhỏ nhất của d là 

Câu 41:

Đồ thị hàm số $y=\frac{x+2}{3 x+9}$ có đường tiệm cận đứng là x=a và đường tiệm cận ngang là y=b. Giá trị của số nguyên m nhỏ nhất thỏa mãn $m \geq a+b$ là 

Câu 42:

Xác định m để đồ thị hàm số $y=\frac{x-1}{x^{2}+2(m-1) x+m^{2}-2}$ có đúng hai tiệm cận đứng 

Câu 43:

Xác định m để đồ thị hàm số $y=\frac{3}{4 x^{2}+2(2 m+3) x+m^{2}-1}$ có đúng hai tiệm cận đứng.

Câu 44:

Xác định m để đồ thị hàm số $y=\frac{x^{2}-(2 m+3) x+2(m-1)}{x-2}$ không có tiệm cận đứng

Câu 45:

Đồ thị hàm số $y=\frac{\sqrt{x^{2}-x+1}+m x}{x-1}$ có đường tiệm cận đứng khi 

Câu 46:

Đồ thị hàm số $y=\frac{\sqrt{x^{2}+2 x+2}-m x}{x+2}$ có hai đường tiệm cận ngang với 

Câu 47:

Giá trị của m để đồ thị hàm số $y=\frac{x-m}{m x-1}$ không có tiệm cận đứng là 

Câu 48:

Cho hàm số y =f(x) có bảng biến thiên 

Số tiệm cận đứng của đồ thị hàm số $y=\frac{2018}{f(x)}$ là

Câu 49:

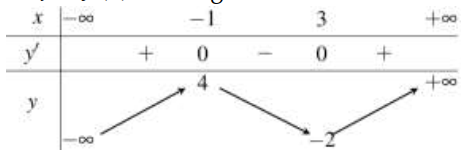
Cho hàm số $f(x)=\frac{a x-b}{c x+b+1}(a, b, c \in \mathbb{R})$ có bảng biến thiên như sau: 

Biết tập hợp tất cả các giá trị b thoả mãn là khoảng $(m: n) \text { . Tính tổng } S=m+2 n$

Câu 50:

Cho hàm số $f(x)=\frac{a x+3}{b x+c},(b \in \mathbb{Z})$ có bảng biến thiên như sau:

$\text { Tính tông } S=a+b+c \text { . }$