Trắc nghiệm Khái niệm về mặt tròn xoay Toán Lớp 12
-
Câu 1:
Cho số thực dương a, kí hiệu H là hình phẳng giới hạn bởi đồ thị hàm số y = 4(x−a)ex, trục hoành và trục tung. Gọi V là thể tích của khổi tròn xoay tạo thành khi quay H quanh trục hoành, tìm a biết V = 4π(e2 − 5).
A. a = 4
B. a = 6
C. a = 1
D. a = 2
-
Câu 2:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a2a và đường cao \(SA = a\sqrt 3 .\). Mặt phẳng (P) vuông góc với SA tại trung điểm M của SA cắt SB, SC, SD lần lượt tại N,P,Q. Xét hình trụ có đáy là đường tròn ngoại tiếp MNPQ và đường sinh MA thì thể tích khối trụ này có giá trị là
A. \(\frac{{\sqrt 3 \pi {a^3}}}{2}\)
B. \(\frac{{\sqrt 3 \pi {a^3}}}{4}\)
C. \(\pi {a^3}\)
D. \(\frac{{\pi {a^3}}}{4}\)
-
Câu 3:
Một khối trụ có thể tích là 25 (đvtt). Nếu tăng bán kính lên 33 lần thì thể tích khối trụ mới tăng lên bao nhiêu lần?
A. 3
B. 9
C. 27
D. 6
-
Câu 4:
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi O là tâm đáy, M là trung điểm của OA. Tính khoảng cách từ điểm M đến mặt phẳng (SCD).
A. \(\frac{{a\sqrt 6 }}{9}\)
B. \({a\sqrt 6 }\)
C. \(\frac{{a\sqrt 6 }}{4}\)
D. \(\frac{{a\sqrt 6 }}{6}\)
-
Câu 5:
Cho a,b là hai số dương. Gọi K là hình phẳng nằm trong góc phần tư thứ hai, giới hạn bởi parabol y=ax2 và đường thẳng y = −bx. Thể tích khối tròn xoay tạo được khi quay K xung quanh trục hoành là một số không phụ thuộc và giá trị của a và b nếu a và b thỏa mãn điều kiện sau
A. \({b^5} = {a^3}\)
B. \({b^4} = 2{a^2}\)
C. \({b^4} = {a^3}\)
D. \({b^3} = {a^5}\)
-
Câu 6:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA = 2a. Góc giữa (SAB) và đáy bằng 60o, góc giữa (SBC) và đáy bằng 45o. Tính thể tích khối chóp S.ABCD' biết chân đường cao hạ từ S nằm trong hình vuông ABCD.
A. \(\frac{{16{a^3}}}{7}\left( {dvtt} \right)\)
B. \(\sqrt 2 {a^3}(dvtt)\)
C. \(\frac{{16{a^3}}}{21}\left( {dvtt} \right)\)
D. 2a3 (dvtt)
-
Câu 7:
Gọi D là miền phẳng giới hạn bởi đồ thị các hàm số \(y = \sqrt {\cos x} ,y = 0,x = 0\) và \(x = \frac{\pi }{4}\). Tính thể tích của khối tròn xoay khi quay D quanh trục hoành.
A. \(\frac{{\sqrt 2 \pi }}{2}\)
B. \({\sqrt 2 \pi }\)
C. \(\frac{\pi }{2}\)
D. \(\frac{\pi }{{2\sqrt 2 }}\)
-
Câu 8:
Cho hình chóp S.ABC có SA = 8, SA vuông góc với đáy. Tam giác ABC vuông tại A, BC = 7. Tính bán kính của mặt cầu ngoại tiếp khối chóp.
A. \(\frac{{\sqrt {113} }}{3}\)
B. \(\frac{{\sqrt {113} }}{4}\)
C. \(\frac{{\sqrt {113} }}{2}\)
D. \({\sqrt {113} }\)
-
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAD là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SC là
A. \(\frac{{a\sqrt 3 }}{{21}}\)
B. \(\frac{{2a\sqrt 3 }}{{21}}\)
C. \(\frac{{a\sqrt 3 }}{{7}}\)
D. \(\frac{{a\sqrt 21 }}{{7}}\)
-
Câu 10:
Cho hình chóp tứ giác đều có cạnh đáy bằng a, mặt bên tạo với mặt đáy một góc 600. Diện tích xung quanh của hình nón ngoại tiếp hình chóp là
A. \(\frac{{\pi {a^2}\sqrt {10} }}{4}\)
B. \(\frac{{\pi {a^2}\sqrt {10} }}{2}\)
C. \(\frac{{\pi {a^2}\sqrt {5} }}{2}\)
D. \(\frac{{\pi {a^2}\sqrt {5} }}{4}\)
-
Câu 11:
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO = h;OB = R;OH = x (0 < x < h). Tìm thể tích lớn nhất của hình trụ.
.png)
A. \(\frac{{2\pi {R^2}h}}{{27}}\)
B. \(\frac{{4\pi {R^2}h}}{{27}}\)
C. \(\frac{{2\pi {R^2}h}}{{9}}\)
D. \(\frac{{4\pi {R^2}h}}{{9}}\)
-
Câu 12:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = 2a, AC = 2a. Hình chiếu của SS lên mặt phẳng (ABC) là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy (ABC) một góc 45o. Khoảng cách từ A đến mặt phẳng (SBC) là:
A. \(\frac{{2\sqrt 5 a}}{{\sqrt {11} }}\)
B. \(\frac{{\sqrt 5 a}}{{\sqrt {11} }}\)
C. \(\frac{{\sqrt 3 a}}{{\sqrt {11} }}\)
D. \(\frac{2{\sqrt 3 a}}{{\sqrt {11} }}\)
-
Câu 13:
Cho hình chóp S.ABC có ABC là tam giác vuông cân tại B, \(AB = BC = 2a,\widehat {SAB} = \widehat {SCB} = {90^o}.\) Và khoảng cách từ A đến mặt phẳng (SBC) bằng \(a\sqrt 2 \). Tính diện tích mặt cầu ngoại tiếp S.ABC theo a.
A. \(6\pi {a^2}\)
B. \(4\pi {a^2}\)
C. \(3\pi {a^2}\)
D. \(12\pi {a^2}\)
-
Câu 14:
Cho tam giác vuông cân ABC với AB = AC = a. Khi quay tam giác đó (cùng với phần trong của nó) quanh đường thẳng đi qua B và song song với AC, ta được khối tròn có thể tích bằng
A. \(\frac{{2\pi {a^3}}}{3}\)
B. \(\frac{{2\pi {a^3}}}{5}\)
C. \(\frac{{\pi {a^3}}}{2}\)
D. \(\frac{{\pi {a^3}}}{3}\)
-
Câu 15:
Thể tích vật thể tròn xoay được giới hạn bởi các đường \(y = \sqrt {1 - {x^2}} ,y = 0,x = 0\) khi quay quanh trục Oy là
A. \(\frac{4}{3}\)
B. \(\frac{{4\pi }}{3}\)
C. \(\frac{{2 }}{3}\)
D. \(\frac{{2\pi }}{3}\)
-
Câu 16:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Biết khoảng cách từ A đến mặt phẳng (SBD) bằng \(a\sqrt 3 .\) Tính khoảng cách từ C đến mặt phẳng (SBD).
A. \(a\sqrt 3 \)
B. \(\frac{{a\sqrt 3 }}{3}\)
C. a
D. \(\frac{{a\sqrt 3 }}{2}\)
-
Câu 17:
Cho hình chóp S.ABCD có đáy là hình chữ nhật, các mặt (SAB) và (SAD) vuông góc với đáy. Góc giữa (SCD) và mặt đáy bằng 600,BC=a. Tính khoảng cách giữa AB và SC theo a.
A. \(\frac{{a\sqrt 3 }}{4}\)
B. \(\frac{{a\sqrt 2 }}{3}\)
C. \({a\sqrt 3 }\)
D. \(\frac{{a\sqrt 3 }}{2}\)
-
Câu 18:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh aa, SA⊥(ABCD). Kẻ AH⊥SB; AK⊥SD. Mặt phẳng (AHK) cắt SC tại I. Tính thể tích khối cầu ngoại tiếp khối ABCDIHK
A. \(\frac{{\pi {a^3}}}{{6\sqrt 3 }}\)
B. \(\frac{{\pi {a^3}}}{{3\sqrt 2 }}\)
C. \(\frac{{\sqrt 2 }}{3}\pi {a^3}\)
D. \(\frac{{2\sqrt 2 }}{3}\pi {a^3}\)
-
Câu 19:
Cho một khối chóp có thể tích bằng V. Khi giảm chiều cao của hình chóp xuống 2 lần và tăng diện tích đáy lên 4 lần thì thể tích khối chóp lúc đó bằng
A. \(\frac{{2V}}{3}\)
B. 3V
C. 2V
D. \(\frac{{V}}{2}\)
-
Câu 20:
Cho hình nón đỉnh S có đường tròn đáy bán kính bằng a, nội tiếp trong hình vuông ABCD. Biết SA = 2a. Tính thể tích của khối chóp S.ABCD.
A. \(\frac{{{a^3}\sqrt 2 }}{6}\)
B. \(\frac{{{a^3}\sqrt 2 }}{3}\)
C. \(\frac{4{{a^3}\sqrt 2 }}{3}\)
D. \(\frac{{{2a^3}\sqrt 2 }}{3}\)
-
Câu 21:
Cho hình chóp S.ABC có AB,AC,SA đôi một vuông góc với nhau, AB = a, AC = 2a, SA = 3a. Tính thể tích của khối chóp S.ABC.
A. 2a3
B. 3a3
C. \(\frac{1}{2}{a^3}\)
D. a3
-
Câu 22:
Cho tam giác ABC vuông tại A, AB = 6, AC = 8. Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là
A. \(\frac{{384}}{5}\pi \)
B. \(\frac{{96}}{3}\pi \)
C. \(\frac{{1152}}{5}\pi \)
D. \(96\pi \)
-
Câu 23:
Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O;R),(O′;R). Biết rằng tồn tại dây cung AB của đường tròn O sao cho O′AB là tam giác đều và (O′AB) hợp với đường tròn O một góc 60o.60o. Tính diện tích xung quanh của hình trụ.
A. \(\frac{{6\pi \sqrt 7 {R^2}}}{7}\)
B. \(\frac{{2\pi \sqrt 7 {R^2}}}{7}\)
C. \(\frac{{\pi \sqrt 7 {R^2}}}{7}\)
D. \(\frac{{4\pi \sqrt 7 {R^2}}}{7}\)
-
Câu 24:
Cho a > b > 0. Đường elip (E) có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1.\) Diện tích của hình elip (E) là
A. \(\pi ab\)
B. \(\frac{{{a^2} + {b^2}}}{2}\pi \)
C. \(2\pi ab\)
D. \(4\pi ab\)
-
Câu 25:
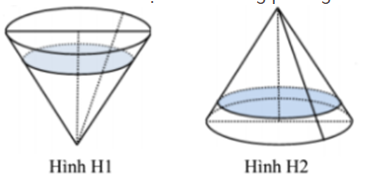
Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng 10 cm (Hình H1). Nếu bịt kín miệng phễu rồi lật ngược phễu lên (Hình H2) thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây ?
A. \( \left( {20\sqrt[3]{7} - 10} \right)cm\)
B. \(\sqrt[3]{7} cm\)
C. \( \left( {20 - 10\sqrt[3]{7}} \right)cm\)
D. \(1cm\)
-
Câu 26:
Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a . Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chiều dài đường sinh bằng 2a thì bán kính đáy bằng:
A. \( \frac{a}{{\pi }}\)
B. \( \frac{a}{{2 }}\)
C. \( \frac{a}{{2\pi }}\)
D. \({2\pi a }\)
-
Câu 27:
Cho lăng trụ đứng ABCA’B’C’ có đáy là tam giác đều cạnh a . Mặt phẳng (AB’C’) tạo với mặt đáy một góc 600. Thể tích khối lăng trụ ABCA’B’C’ theo a bằng:
A. \( \frac{{3{a^3}\sqrt 3 }}{8}\)
B. \( \frac{{{a^3}\sqrt 3 }}{8}\)
C. \( \frac{{3{a^3}\sqrt 2}}{8}\)
D. \( \frac{{{a^3}\sqrt 2}}{8}\)
-
Câu 28:
Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng \(a\sqrt6\). Tính thể tích V của khối nón đó?
A. \( \frac{{\pi \sqrt 6 {a^3}}}{4}.\)
B. \( \frac{{\pi \sqrt 6 {a^3}}}{2}.\)
C. \( \frac{{\pi \sqrt 3 {a^3}}}{4}.\)
D. \( \frac{{\pi \sqrt 3{a^3}}}{2}.\)
-
Câu 29:
Trong không gian, cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính diện tích toàn phần Stp của hình nón khi quay tam giác ABC xung quanh trục AC.
A. 4π
B. 24π
C. 72π
D. 48π
-
Câu 30:
Một chiếc hộp hình trụ với bán kính đáy bằng chiều cao và bằng 10 cm. Một học sinh bỏ một miếng bìa hình vuông vào chiếc hộp đó và thấy hai cạnh đối diện của miếng bìa lần lượt là các dây cung của hai đường tròn đáy hộp và miếng bìa không song song với trục của hộp. Hỏi diện tích của miếng bìa đó bằng bao nhiêu?
A. \(150cm^3\)
B. \(250cm^3\)
C. \(200cm^3\)
D. \(220cm^3\)
-
Câu 31:
Mệnh đề nào dưới đây đúng? Cho hình chữ nhật ABCD có AB = 2AD. Quay hình chữ nhật đã cho quanh AD và AB ta được hai hình trụ tròn xoay có thể tích lần lượt là V1, V2.
A. \(V_1=4V_2\)
B. \(V_2=4V_1\)
C. \(V_2=2V_1\)
D. \(V_1=2V_2\)
-
Câu 32:
Trong một chiếc hộp hình trụ người ta bỏ vào đó 6 quả banh tennis, biết rằng đáy của hình trụ bằng hình tròn lớn trên quả banh và chiều cao hình trụ bằng 6 lần đường kính của quả banh. Gọi V1 là tổng thể tích của 6 quả banh và V2 là thể tích của khối trụ. Tính tỉ số \( \frac{{{V_1}}}{{{V_2}}}\)?
A. \( \frac{1}{3}.\)
B. \( \frac{2}{3}.\)
C. \( \frac{1}{2}.\)
D. \(2\)
-
Câu 33:
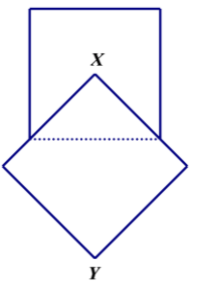
Cho hai hình vuông cùng có cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại (như hình vẽ bên). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY.
A. \( V = \frac{{125\left( {1 + \sqrt 2 } \right)\pi }}{6}\)
B. \( V = \frac{{125\left( {5 + 2\sqrt 2 } \right)\pi }}{{12}}\)
C. \( V = \frac{{125\left( {5 + 4\sqrt 2 } \right)\pi }}{{12}}\)
D. \( V = \frac{{125\left( {2 + 2\sqrt 2 } \right)\pi }}{{12}}\)
-
Câu 34:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Tính diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A’B’C’D’ và đáy là hình tròn nội tiếp hình vuông ABCD.
A. \(\frac{{\pi {a^2}\sqrt {17} }}{4}.\)
B. \(\frac\pi {a^2}\)
C. \(\frac{{\pi {a^2}\sqrt {17} }}{2}.\)
D. \(\frac{\pi} {a^2\sqrt {17}}\)
-
Câu 35:
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có \( AB = AD = 2a,AA' = 3\sqrt 2 a.\). Tính điện tích toàn phần S của hình trụ có hai đáy lần lượt ngoại tiếp hai đáy của hình hộp chữ nhật đã cho.
A. \(16\pi {a^2}.\)
B. \(20\pi {a^2}.\)
C. \(7\pi {a^2}.\)
D. \(12\pi {a^2}.\)
-
Câu 36:
Cho hình trụ có hai đường tròn đáy lần lượt là (O); (O’). Biết thể tích khối nón có đỉnh là O và đáy là hình tròn (O’) là a3. Tính thể tích V của khối trụ đã cho?
A. V=2a3
B. V=4a3
C. V=6a3
D. V=3a3
-
Câu 37:
Một tam giác ABC vuông tại A có AB = 6, AC = 8. Cho đường gấp khúc ABC quay quanh cạnh AC được hình nón có diện tích xung quanh và diện tích toàn phần lần lượt là S1, S2. Hãy chọn kết quả đúng.
A. \( \frac{1}{8}\)
B. \( \frac{5}{8}\)
C. \( \frac{5}{7}\)
D. \( \frac{2}{3}\)
-
Câu 38:
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB =3, AD = 4 , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SC và mặt phẳng đáy là \(45^0\). Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD .
A. \(\frac{ \sqrt{2}}{2} \text {. }\)
B. \(\frac{5 \sqrt{2}}{2} \text {. }\)
C. \(\frac{\sqrt{3}}{2} \text {. }\)
D. \(\frac{5 \sqrt{3}}{2} \text {. }\)
-
Câu 39:
Cho khối nón có thể tích là V . Biết rằng khi cắt khối nón đã cho bởi một mặt phẳng qua trục, thiết diện thu được là một tam giác đều có diện tích bằng 3 . Giá trị của V bằng
A. \(3 \pi \sqrt{3}\)
B. \(5 \pi \sqrt{3}\)
C. \(\frac{1}{3} \pi \sqrt{3}\)
D. \(\frac{1}{5} \pi \sqrt{3}\)
-
Câu 40:
Tính diện tích toàn phần S của mặt nón (N) biết thiết diện qua trục của nó là một tam giác vuông có cạnh huyền bằng \(2\sqrt 2a\)
A. \((2 \sqrt{2}+2) \pi a^{2}\)
B. \((2 \sqrt{2}-1) \pi a^{2}\)
C. \((1-2 \sqrt{2}) \pi a^{2}\)
D. \(2 \sqrt{2}\pi a^{2}\)
-
Câu 41:
Cho hình nón có độ dài đường sinh \(l=4\) và bán kính đáy \(r=\frac{1}{4}\) . Diện tích xung quanh của hình nón bằng
A. \(2\pi\)
B. \(\pi\)
C. \(3\pi\)
D. \(4\pi\)
-
Câu 42:
Cho hình trụ có bán kính đáy \(r=\sqrt 3\) và chiều cao h=4 . Diện tích xung quanh của hình trụ bằng.
A. \(4\pi \sqrt{3}\)
B. \(9 \pi \sqrt{3}\)
C. \( \pi \sqrt{3}\)
D. \(8 \pi \sqrt{3}\)
-
Câu 43:
Cho khối nón có bán kính đáy là r = 2 và chiều cao \(h=\sqrt3\) . Tính thể tích của khối nón đã cho là?
A. \(\frac{4 \pi \sqrt{3}}{3} \text {. }\)
B. \(\frac{3 \pi \sqrt{3}}{3} \text {. }\)
C. \(\frac{2 \pi \sqrt{3}}{3} \text {. }\)
D. \(\frac{ \pi \sqrt{3}}{3} \text {. }\)
-
Câu 44:
Hình nón có đường sinh bằng 6 , diện tích xung quanh bằng \(12\pi\) . Bán kính đường tròn đáy của hình nón đó bằng
A. 1
B. 2
C. 3
D. 4
-
Câu 45:
Cho hình chữ nhật ABCD(kể cả miền trong), quay hình chữ nhật đó quanh một cạnh thì thể tích vật thể tròn xoay được tạo thành là:
A. Hình trụ.
B. Khối nón.
C. Khối trụ.
D. Hình nón.
-
Câu 46:
Cho tam giác ABH vuông tại H , AH=3a , BH=2a. Quay tam giác ABH quanh trục AH ta được một khối nón có thể tích là:
A. \(4 \pi a^{3} \text {. }\)
B. \(4 \sqrt 3\pi a^{3} \text {. }\)
C. \(2\sqrt 3 \pi a^{3} \text {. }\)
D. \(2 \pi a^{3} \text {. }\)
-
Câu 47:
Cho góc ở đỉnh của một hình nón bằng 60o . Gọi \(r, h, l \) lần lượt là bán kính, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
A. \(l=2r\)
B. \(h=r\)
C. \(h=2r\)
D. \(l=r\)
-
Câu 48:
Cắt hình trụ (T) bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông cạnh bằng 10. Diện tích xung quanh của (T) là
A. \(50\sqrt 3 \pi\)
B. \(100 \pi\)
C. \(125 \pi\)
D. \(50 \pi\)
-
Câu 49:
Cho khối nón có bán kính đáy r=a và chiều cao h =2a . Thể tích của khối nón đã cho bằng
A. \(\frac{2 \pi a^{3}}{3} \text {. }\)
B. \(\frac{ \pi a^{3}}{3} \text {. }\)
C. \(\frac{2\sqrt 3 \pi a^{3}}{3} \text {. }\)
D. \(\frac{\sqrt 2 \pi a^{3}}{3} \text {. }\)
-
Câu 50:
Cho hình lăng trụ có đường kính đáy bằng 6cm , độ dài đường cao bằng 4cm . Tính diện tích xung quanh của hình trụ này
A. \(12 \pi \mathrm{cm}^{2}\)
B. \(24 \pi \mathrm{cm}^{2}\)
C. \(5 \pi \mathrm{cm}^{2}\)
D. \(7\sqrt 3 \pi \mathrm{cm}^{2}\)
