Trắc nghiệm Cực trị của hàm số Toán Lớp 12
-
Câu 1:
Cho hàm số f(x)f(x) có đạo hàm trên thỏa mãn |f(x+h)–f(x–h)|≤h2|f(x+h)–f(x–h)|≤h2 với mọi , h > 0. Đặt g(x)=[x+f′(x)]2019+[x+f′(x)]29–m–(m4–29m2+100).sin2x–1g(x)=[x+f′(x)]2019+[x+f′(x)]29–m–(m4–29m2+100).sin2x–1 với tham số m. Gọi S là tập hợp tất cả các giá trị nguyên của m < 27 sao cho g(x)g(x) đạt cực tiểu tại x = 0. Tổng bình phương các phần tử của S là
A. 100
B. 50
C. 108
D. 58
-
Câu 2:
Cho hàm số y=f(x)y=f(x) liên tục và xác định trênvà có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để hàm số y=|(f(x))2+2mf(x)+2m+35|y=∣∣(f(x))2+2mf(x)+2m+35∣∣ có đúng 3 điểm cực trị
.jpg.png)
A. 5
B. 6
C. 7
D. 8
-
Câu 3:
Có bao nhiêu giá trị nguyên của tham số m để hàm số y=x8+(m–2)x5–(m2–4)x4+1y=x8+(m–2)x5–(m2–4)x4+1 đạt cực tiểu tại x = 0
A. 4
B. 3
C. 5
D. Vô số
-
Câu 4:
Cho hai hàm đa thức y=f(x),y=g(x)y=f(x),y=g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y=f(x)y=f(x) có đúng một điểm cực trị là A, đồ thị hàm số y=g(x)y=g(x) có đúng một điểm cực trị là B và AB=74AB=74. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (–5;5)(–5;5) để hàm số y=||f(x)–g(x)|+m|y=||f(x)–g(x)|+m| có đúng 5 điểm cực trị?
.jpg.png)
A. 1
B. 6
C. 4
D. 3
-
Câu 5:
Cho hàm số bậc ba y=f(x)y=f(x) có đồ thị của hàm đạo hàm f′(x)f′(x) như hình vẽ và f(b)=1f(b)=1. Số giá trị nguyên của m∈[–5;5]m∈[–5;5] để hàm số g(x)=|f2(x)+4f(x)+m|g(x)=∣∣f2(x)+4f(x)+m∣∣ có đúng 5 điểm cực trị là
.jpg.png)
A. 9
B. 7
C. 8
D. 10
-
Câu 6:
Cho hàm số bậc bốn f(x) có bảng biến thiên như sau
.png)
Số điểm cực trị của hàm số g(x)=x2[f(x+1)]4g(x)=x2[f(x+1)]4
A. 11
B. 9
C. 7
D. 5
-
Câu 7:
Cho hàm số y=f(x)y=f(x), hàm số y=f′(x)y=f′(x) có đồ thị như hình bên. Hàm số g(x)=2f(5sinx–12)+(5sinx–1)24+3g(x)=2f(5sinx–12)+(5sinx–1)24+3 có bao nhiêu điểm cực trị trên khoảng (0;2π)(0;2π).
.jpg.png)
A. 9
B. 7
C. 6
D. 8
-
Câu 8:
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y=x4+2mx2+1y=x4+2mx2+1 có ba điểm cực trị tạo thành một tam giác vuông cân.
A. m = 1
B. m = – 1
C. m=–13√9m=–13√9
D. m=13√9m=13√9
-
Câu 9:
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y=x3+2x2+(m–3)x+my=x3+2x2+(m–3)x+m có hai điểm cực trị và điểm M(9;–5)M(9;–5) nằm trên đường thẳng đi qua hai điểm cực trị của đồ thị.
A. m = – 10
B. m = 10
C. m = 2
D. m = 3
-
Câu 10:
Cho hàm số f(x)f(x) có đạo hàm f′(x)=x2(x+1)(x2+2mx+5)f′(x)=x2(x+1)(x2+2mx+5). Có tất cả bao nhiêu giá trị nguyên của m để hàm số có đúng một điểm cực trị?
A. 0
B. 5
C. 6
D. 7
-
Câu 11:
Có bao nhiêu giá trị nguyên của tham số m để hàm số y=m2x4–(m2–2019m)x2–1y=m2x4–(m2–2019m)x2–1 có đúng một cực trị.
A. 2019
B. 2020
C. 2018
D. 2021
-
Câu 12:
Biết rằng hàm số y=(x+a)3+(x+b)3–x3y=(x+a)3+(x+b)3–x3 có hai điểm cực trị. Mệnh đề nào sau đây là đúng?
A. ab≥0ab≥0
B. ab≤0ab≤0
C. ab > 0
D. ab < 0
-
Câu 13:
Cho hàm số y=f(x)y=f(x) xác định trên tập số thực RR và có đạo hàm f′(x)=(x–sinx)(x–m–3)(x–√9–m2)3∀x∈Rf′(x)=(x–sinx)(x–m–3)(x–√9–m2)3∀x∈R (m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số y=f(x)y=f(x) đạt cực tiểu tại x = 0?
A. 6
B. 4
C. 5
D. 7
-
Câu 14:
Cho hàm số f′(x)=(x–2)2(x2–4x+3)f′(x)=(x–2)2(x2–4x+3) với mọi x∈Rx∈R. Có bao nhiêu giá trị nguyên dương của m để hàm số y=f(x2–10x+m+9)y=f(x2–10x+m+9) có 5 điểm cực trị
A. 18
B. 16
C. 15
D. 19
-
Câu 15:
Cho hàm số y=f(x)y=f(x) là một hàm đa thức có bảng xét dấu f′(x)f′(x) như sau
.png)
Số điểm cực trị của hàm số g(x)=f(x2–|x|)g(x)=f(x2–|x|)
A. 5
B. 3
C. 1
D. 7
-
Câu 16:
Cho hàm số y=f(x)y=f(x) liên tục trên RR có đạo hàm f′(x)f′(x) liên tục trên RR và có bảng xét dấu như hình vẽ bên
.png)
Hỏi hàm số y=f(x2–2|x|)y=f(x2–2|x|) có tất cả bao nhiêu điểm cực trị
A. 4
B. 7
C. 9
D. 11
-
Câu 17:
Cho hàm số y=x4–2mx2+my=x4–2mx2+m. Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
A. m > 0
B. m < 0
C. m≥0m≥0
D. m≤0m≤0
-
Câu 18:
Tìm giá trị thực của tham số m để hàm số y=13x3–mx2+(m2–4)x+3y=13x3–mx2+(m2–4)x+3 đạt cực đại tại x = 3.
A. m = 1
B. m = – 7
C. m = 5
D. m = – 1
-
Câu 19:
Số điểm cực trị của hàm số y=x+√2x2+1y=x+√2x2+1 là
A. 1
B. 2
C. 3
D. 0
-
Câu 20:
Đồ thị của hàm số y=–x3+3x2+9x+1y=–x3+3x2+9x+1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB ?
A. M(1;–12)M(1;–12)
B. N(1;12)N(1;12)
C. P(1;0)P(1;0)
D. Q(0;–1)Q(0;–1)
-
Câu 21:
Cho hàm số y=f(x)y=f(x) có đồ thị hình bên. Hàm số y=f(|x|)y=f(|x|) có bao nhiêu điểm cực trị?
.jpg.png)
A. 3
B. 2
C. 5
D. 1
-
Câu 22:
Biết rằng đồ thị hàm số y=x3+3x2y=x3+3x2 có dạng như hình vẽ:
.jpg.png)
Hỏi đồ thị hàm số y=|x3+3x2|y=∣∣x3+3x2∣∣ có bao nhiêu điểm cực trị?
A. 0
B. 2
C. 1
D. 3
-
Câu 23:
Cho hàm số y=f(x)y=f(x) liên tục trên RR, đồ thị của đạo hàm f′(x)f′(x) như hình vẽ sau:
.jpg.png)
Trong các mệnh đề sau, mệnh đề nào sai?
A. f đạt cực tiểu tại x = 0
B. f đạt cực tiểu tại x = – 2
C. f đạt cực đại tại x = – 2
D. Cực tiểu của f nhỏ hơn cực đại.
-
Câu 24:
Cho hàm số y=f(x)y=f(x) xác định trên RR và có đồ thị hàm số y=f′(x)y=f′(x) là đường cong ở hình bên. Hỏi hàm số y=f(x)y=f(x) có bao nhiêu điểm cực trị ?
.jpg.png)
A. 6
B. 3
C. 4
D. 5
-
Câu 25:
Cho hàm số y=f(x)y=f(x) liên tục trên RR và có đạo hàm f′(x)=(x–1)(x–2)2(x–3)53√x–4f′(x)=(x–1)(x–2)2(x–3)53√x–4. Hỏi hàm số y=f(x)y=f(x) có bao nhiêu điểm cực trị?
A. 2
B. 4
C. 3
D. 5
-
Câu 26:
Cho hàm số y=f(x)y=f(x) có bảng biến thiên như hình vẽ. Hàm số có bao nhiêu điểm cực trị?
.png)
A. 2
B. 3
C. 4
D. 5
-
Câu 27:
Hàm số y=f(x)y=f(x) có đạo hàm f′(x)=(x–1)(x–2)…(x–2019),∀x∈Rf′(x)=(x–1)(x–2)…(x–2019),∀x∈R. Hàm số y=f(x)y=f(x) có tất cả bao nhiêu điểm cực tiểu?
A. 1009
B. 2019
C. 2020
D. 1010
-
Câu 28:
Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A. y=x4y=x4
B. y=–x3+xy=–x3+x
C. y=2x–3x+2y=2x–3x+2
D. y=|x+2|y=|x+2|
-
Câu 29:
Gọi x1x1 là điểm cực đại, x2x2 là điểm cực tiểu của hàm số y=x3–3x+2y=x3–3x+2. Tính x1+2x2x1+2x2.
A. 2
B. – 1
C. 0
D. 1
-
Câu 30:
Cho hàm số y=x2+16xy=x2+16x. Mệnh đề nào dưới đây đúng?
A. Cực tiểu của hàm số bằng 12
B. Cực tiểu của hàm số bằng 2
C. Cực đại của hàm số bằng 12
D. Cực đại của hàm số bằng 2
-
Câu 31:
Cho hàm số y=f(x)y=f(x) có đạo hàm là f′(x)=x(x+1)2(x–1)f′(x)=x(x+1)2(x–1). Hàm số y=f(x)y=f(x) có bao nhiêu điểm cực trị?
A. 2
B. 0
C. 1
D. 3
-
Câu 32:
Cho hàm số y = f(x) có đồ thị như hình bên. Hàm số có bao nhiêu điểm cực tiểu trên khoảng (a;b)(a;b)?
.jpg.png)
A. 3
B. 0
C. 1
D. 4
-
Câu 33:
Cho hàm số y=f(x)y=f(x) có bảng biến thiên như hình bên.
.png)
Tọa độ điểm cực đại của đồ thị hàm số y=f(x)y=f(x) là
A. (1;–4)(1;–4)
B. x = 0
C. (–1;–4)(–1;–4)
D. (0;–3)(0;–3)
-
Câu 34:
Cho hàm số y=f(x)y=f(x) xác định trên và có bảng xét dấu của đạo hàm như sau.
.png)
Khi đó số điểm cực trị của hàm số y=f(x)y=f(x) là
A. 3
B. 2
C. 4
D. 1
-
Câu 35:
Hàm số y=f(x)y=f(x) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
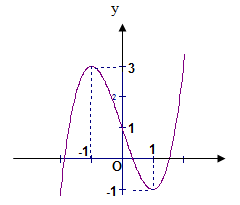
A. Đồ thị hàm số có điểm cực đại là (1;–1)(1;–1)
B. Đồ thị hàm số có điểm cực tiểu là (1;–1)(1;–1)
C. Đồ thị hàm số có điểm cực tiểu là (–1;3)(–1;3)
D. Đồ thị hàm số có điểm cực tiểu là (1;1)(1;1)
-
Câu 36:
Cho hàm số y=f(x)y=f(x) liên tục trên RR và có bảng biến thiên:
.png)
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x = 0.
B. Hàm số có đúng hai điểm cực trị.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng – 3.
D. Hàm số có giá trị cực tiểu bằng – 1 và 1.
-
Câu 37:
Cho hàm số f(x)f(x) có bảng biến thiên như sau:
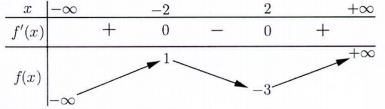
Điểm cực đại của hàm số đã cho là:
A. x = – 3
B. x = 1
C. x = 2
D. x = – 2
-
Câu 38:
Tìm tất cả các giá trị thực của tham số m để hàm số y=mx4+(m2−9)x2+10y=mx4+(m2−9)x2+10 có 3 điểm cực trị.
A. [0<m<3m<−3
B. [0<m<3m≤−3
C. m<-3
D. m≤−3
-
Câu 39:
Tìm tất cả các giá trị của tham số m để hàm số y=13x3−mx2+(2m−1)x−3 có cực trị.
A. m≠1
B. ∀m
C. m≤1.
D. m≥1.
-
Câu 40:
Cho hàm số y=14x4−2x2+3 . Diện tích tam giác có các đỉnh là các điểm cực trị của đồ thị ( C) là:
A. m=8
B. m=16
C. m=32
D. m=64
-
Câu 41:
Tìm các giá trị của tham số m để đồ thị hàm số: y=x4−2m2x2+1 có ba điểm cực trị là ba
đỉnh của một tam giác vuông cân?A. m=-1
B. m≠0
C. m=1
D. m=±1
-
Câu 42:
Tìm các giá trị của tham số m để hàm số y=mx4+(m2−4m+3)x2+2m−1 có ba điểm cực trị
A. m∈(−∞;0).
B. m∈(0;1)∪(3;+∞).
C. m∈(−∞;0)∪(1;3).
D. m∈(1;3).
-
Câu 43:
Tìm các giá trị của tham số m để hàm số y=mx4+(m−1)x2+m chỉ có đúng một cực trị?
A. 0<m≤1.
B. [m<0m≥1.
C. [m≤0m≥1
D. 0≤m≤1 .
-
Câu 44:
Tìm các giá trị của tham số m để hàm số: y=13mx3−(m−1)x2+3(m−2)x+16 đạt cực trị tại x1,x2, thỏa mãn x1+2x2=1?
A. 1−√62<m<1+√62
B. [m=23m=2
C. m∈(1−√62;1+√62)∖{0}.
D. m=2.
-
Câu 45:
Tìm tất cả các giá trị thực của tham số m để hàm số y=13x3+(m2−m+2)x2+(3m2+1)x đạt cực tiểu tại x=-2?
A. [m=3m=1
B. m=3
C. m=1
D. [m=−3m=−1
-
Câu 46:
ó bao nhiêu giá tị nguyên của tham số m để hàm số y=13x3+(m+3)x2+4(m+3)x+m3−m đạt
cực trị tại x1,x2 thỏa mãn −1<x1<x2A. 2
B. 4
C. 6
D. 8
-
Câu 47:
Tìm tất các giá trị thực của tham số m để hàm số y=13x3+(m+3)x2+4(m+3)x+m3−m đạt cực trị tại x1,x2 thỏa mãn −1<x1<x2
A. −72<m<−2
B. −3<m<1
C. [m<−3m>1
D. −72<m<−3
-
Câu 48:
Tìm tất các giá trị thực của tham số m để hàm số y=(m+2)x3+3x2+mx−6 có hai cực trị?
A. m∈(−3;1)∖{−2}.
B. m∈(−3;2).
C. m∈(−∞;1)∪(2;+∞).
D. m∈[−5;1] .
-
Câu 49:
Tìm tất cả các giá trị thực của tham số m để hàm số y=13x3−mx2+(m+1)x−1 đạt cực đại tại x=-2?
A. -1
B. 2
C. 3
D. Không tồn tại m.
-
Câu 50:
Tìm tất cả các giá trị thực của m để hàm số y=x3−2x2+(m+3)x−1 không có cực trị?
A. m≥−83.
B. m>−53.
C. m≥−53.
D. m≤−83.














