Trắc nghiệm Cực trị của hàm số Toán Lớp 12
-
Câu 1:
Cho hàm số \(y=(m-1) x^{4}-3 m x^{2}+5\) . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu
A. \(m \in(-\infty ; 0] \cup[1 ;+\infty)\)
B. \(m \in[0 ; 1]\)
C. \(m \in(0 ; 1)\)
D. \(m \in(-\infty ; 0) \cup(1 ;+\infty)\)
-
Câu 2:
Gọi \(x_1;x_2\) là hai điểm cực trị của hàm số \(y=x^{3}-3 m x^{2}+3\left(m^{2}-1\right) x-m^{3}+m\) . Tìm tất cả các giá trị của tham số thực m để \(x_{1}^{2}+x_{2}^{2}-x_{1} x_{2}=7\)
A. \(m=\pm \sqrt{2}\)
B. \(m=\pm 2\)
C. \(m=0\)
D. \(m=\pm 1\)
-
Câu 3:
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \(y=\frac{2}{3} x^{3}-m x^{2}-2\left(3 m^{2}-1\right) x+\frac{2}{3}\) có hai điểm cực trị có hoành độ x 1 , x2 sao cho \(x_{1} x_{2}+2\left(x_{1}+x_{2}\right)=1\)
A. m=0
B. \(m=-\frac{2}{3}\)
C. \(m=\frac{2}{3}\)
D. \(m=-\frac{1}{2}\)
-
Câu 4:
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số \(y=-x^{3}+3 m x+1 \text { có }\) điểm cực trị , B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ).
A. \(m=\frac{3}{2}\)
B. \(m=-\frac{1}{2}\)
C. \(m=1\)
D. \(m=\frac{1}{2}\)
-
Câu 5:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=x^{3}-3 m x^{2}+(m-1) x+2\) có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. \(0 \leq m \leq 1\)
B. \(m \geq 1\)
C. \(m \geq 0\)
D. \(m>1\)
-
Câu 6:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=(m+1) x^{4}-m x^{2}+\frac{3}{2}\) chỉ có cực tiểu mà không có cực đại.
A. \(m<-1\)
B. \(-1 \leq m \leq 0\)
C. \(m>1\)
D. \(-1 \leq m<0\)
-
Câu 7:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=m x^{4}+\left(m^{2}-9\right) x^{2}+10\) có 3 điểm cực trị.
A. \(\left[\begin{array}{l}0<m<3 \\ m<-3\end{array}\right.\)
B. \(m<-3\)
C. \(0<m \leq 3\)
D. \(\left[\begin{array}{l}0<m<3 \\ m \leq-3\end{array}\right.\)
-
Câu 8:
Tìm tất cả các giá trị của tham số m để hàm số \(y=\frac{1}{3} x^{3}-m x^{2}+(2 m-1) x-3\) có cực trị
A. \(m \neq 1\)
B. \(\forall m\)
C. \(m \leq 1\)
D. \(m \geq 1\)
-
Câu 9:
Tìm các giá trị của tham số m để đồ thị hàm số: \(y=x^{4}-2 m x^{2}+2 m+m^{4}\) có ba điểm cực trị là ba đỉnh của một tam giác đều.
A. Không tồn tại m
B. \(\left[\begin{array}{ll}m=0 \\ m=\sqrt[3]{3}\end{array}\right.\)
C. \(m=\pm \sqrt{3}\)
D. \(m=\sqrt[3]{3}\)
-
Câu 10:
Tìm các giá trị của tham số m để đồ thị hàm số: \(y=x^{4}-2(m+1) x^{2}+m^{2}\) có ba điểm cực trị là ba đỉnh của một tam giác vuông cân
A. Không tồn tại m
B. m=0
C. \(\left[\begin{array}{l} m=0 \\ m=-1 \end{array}\right.\)
D. m=-1
-
Câu 11:
Tìm các giá trị của tham sốm để đồ thị hàm số: \(y=x^{4}-2 m^{2} x^{2}+1\) có ba điểm cực trị là ba đỉnh của một tam giác vuông cân.
A. m=-1
B. \(m \neq 0\)
C. m=1
D. \(m=\pm 1\)
-
Câu 12:
Tìm các giá trị của tham sốm để hàm số \(y=m x^{4}+\left(m^{2}-4 m+3\right) x^{2}+2 m-1\) có ba điểm cực trị?
A. \(m \in(-\infty ; 0)\)
B. \(m \in(0 ; 1) \cup(3 ;+\infty)\)
C. \(m \in(-\infty ; 0) \cup(1 ; 3)\)
D. \(m \in(1 ; 3)\)
-
Câu 13:
Tìm các giá trị của tham số m để hàm số \(y=m x^{4}+(m-1) x^{2}+m\) chỉ có đúng một cực trị?
A. \(0<m \leq 1\)
B. \(\left[\begin{array}{l}m<0 \\ m \geq 1\end{array}\right.\)
C. \(\left[\begin{array}{l}m \leq 0 \\ m \geq 1\end{array}\right.\)
D. \(0 \leq m \leq 1\)
-
Câu 14:
Tìm các giá trị của tham số m để hàm số: \(y=\frac{1}{3} m x^{3}-(m-1) x^{2}+3(m-2) x+\frac{1}{6}\) đạt cực trị tại \(x_{1}, x_{2}\) thỏa mãn \(x_{1}+2 x_{2}=1\)?
A. \(1-\frac{\sqrt{6}}{2}<m<1+\frac{\sqrt{6}}{2}\)
B. \(\left[\begin{array}{l}m=\frac{2}{3} \\ m=2\end{array}\right.\)
C. \(m \in\left(1-\frac{\sqrt{6}}{2} ; 1+\frac{\sqrt{6}}{2}\right) \backslash\{0\}\)
D. \(m=2\)
-
Câu 15:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{1}{3} x^{3}+\left(m^{2}-m+2\right) x^{2}+\left(3 m^{2}+1\right) x\) đạt cực tiểu tại x=-2?
A. \(\left[\begin{array}{l} m=3 \\ m=1 \end{array}\right.\)
B. m=3
C. m=1
D. \(\left[\begin{array}{l} m=-3 \\ m=-1 \end{array}\right.\)
-
Câu 16:
Tìm tất các giá trị thực của tham số m để hàm số \(y=\frac{1}{3} x^{3}+(m+3) x^{2}+4(m+3) x+m^{3}-m\) đạt cực trị tại \(x_{1}, x_{2}\) thỏa mãn \(-1<x_{1}<x_{2}\)
A. \(-\frac{7}{2}<m<-2\)
B. \(-3<m<1\)
C. \(\left[\begin{array}{l}m<-3 \\ m>1\end{array}\right.\)
D. \(-\frac{7}{2}<m<-3\)
-
Câu 17:
Tìm tất các giá trị thực của tham số m để hàm số \(y=(m+2) x^{3}+3 x^{2}+m x-6\) cực trị ?
A. \(m \in(-3 ; 1) \backslash\{-2\}\)
B. \(m \in(-3 ; 1)\)
C. \(m \in(-\infty ;-3) \cup(1 ;+\infty)\)
D. \(m \in[-3 ; 1]\)
-
Câu 18:
Tìm tất cả các giá trị thực của tham số m để hàm số: \(y=\frac{1}{3} x^{3}+m x^{2}+(m+6) x+m\) có cực đại và cực tiểu
A. \(-2<m<3\)
B. \(\left[\begin{array}{l}m<-2 \\ m>3\end{array}\right.\)
C. \(\left[\begin{array}{l}m \leq-2 \\ m \geq 3\end{array}\right.\)
D. \(-2 \leq m \leq 3\)
-
Câu 19:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{m}{3} x^{3}+2 x^{2}+m x+1\) có 2 điểm cực trị thỏa mãn \(x_{C D}<x_{C T}\)
A. m<2
B. -2<m<0
C. -2<m<2
D. 0<m<2
-
Câu 20:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{1}{3} x^{3}-m x^{2}+(m+1) x-1\) đạt cực đại tại x=-2?
A. -1
B. 2
C. 3
D. Không tồn tại m
-
Câu 21:
Tìm tất cả các giá trị thực của m để hàm số \(y=x^{3}-2 x^{2}+(m+3) x-1\) không có cực trị?
A. \(m \geq-\frac{8}{3}\)
B. \(m>-\frac{5}{3}\)
C. \(m \geq-\frac{5}{3}\)
D. \(m \leq-\frac{8}{3}\)
-
Câu 22:
Tìm tất cả các giá trị thực của m để hàm số \(y=m x^{4}-(m+1) x^{2}+2 m-1\) có 3 điểm cực trị ?
A. \(\left[\begin{array}{l}m<-1 \\ m>0\end{array}\right.\)
B. \(m<-1 .\)
C. \(-1<m<0\)
D. \(m>-1\)
-
Câu 23:
Biết đồ thị hàm số \(y=x^{3}-2 x^{2}+a x+b\) có điểm cực trị là A(1; 3) . Khi đó giá trị của \(4 a-b\) là:
A. 1
B. 2
C. 3
D. 4
-
Câu 24:
Cho hàm số \(y=(m-1) x^{3}-3 x^{2}-(m+1) x+3 m^{2}-m+2\) . Để hàm số có cực đại, cực tiểu thì:
A. m=1
B. m>1
C. \(m \neq 1\)
D. m tùy ý
-
Câu 25:
Hàm số \(y=x^{3}-3 x^{2}+m x-2\) đạt cực tiểu tại x = 2 khi?
A. m>0
B. m=0
C. m<0
D. \(m \neq 0\)
-
Câu 26:
Hàm số \(y=x^{4}+2(m-2) x^{2}+m^{2}-2 m+3\) có đúng 1 điểm cực trị thì giá trị của m là:
A. \(m \geq 2\)
B. m>2
C. m=2
D. m<2
-
Câu 27:
Tìm tất cả các giá trị của tham số m để hàm số \(y=x^{3}-m x^{2}+(2 m-3) x-3\) đạt cực đại tại x = 1.
A. m>3
B. m=3
C. \(m \leq 3\)
D. m<3
-
Câu 28:
Cho hàm số \(y=x^{7}-x^{5}\). Khẳng định nào sau đây là đúng
A. Hàm số có đúng 1 điểm cực trị
B. Hàm số có đúng 3 điểm cực trị.
C. Hàm số có đúng hai điểm cực trị.
D. Hàm số có đúng 4 điểm cực trị.
-
Câu 29:
Trong các hàm số sau, hàm số nào chỉ có cực đại mà không có cực tiểu?
A. \(y=-10 x^{4}-5 x^{2}+7\)
B. \(y=-17 x^{3}+2 x^{2}+x+5\)
C. \(y=\frac{x-2}{x+1}\)
D. \(y=\frac{x^{2}+x+1}{x-1}\)
-
Câu 30:
Trong các hàm số sau, hàm số nào đạt cực đại tại \(x=\frac{3}{2} ?\)
A. \(y=\frac{1}{2} x^{4}-x^{3}+x^{2}-3 x\)
B. \(y=\sqrt{-x^{2}+3 x-2}\)
C. \(y=\sqrt{4 x^{2}-12 x-8}\)
D. \(y=\frac{x-1}{x+2}\)
-
Câu 31:
Cho hàm số \(y=3 x^{4}-6 x^{2}+1\) . Kết luận nào sau đây là đúng?
A. \(y_{C Đ}=-2\)
B. \(y_{C Đ}=1\)
C. \(y_{C Đ}=-1\)
D. \(y_{C Đ}=2\)
-
Câu 32:
Cho hàm số \(y=x^{3}+17 x^{2}-24 x+8\) . Kết luận nào sau đây là đúng?
A. \(x_{C Đ}=1\)
B. \(x_{C Đ}=\frac{2}{3}\)
C. \(x_{C Đ}=-3\)
D. \(x_{C Đ}=-12\)
-
Câu 33:
Cho hàm số \(y=x^{4}-2 x^{2}+3\). Khẳng định nào sau đây là đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số chỉ có đúng 2 điểm cực trị
C. Hàm số không có cực trị.
D. Hàm số chỉ có đúng một điểm cực trị.
-
Câu 34:
Tìm số cực trị của hàm số \(y=\frac{x^{4}}{4}-x^{2}+2\)
A. 0
B. 1
C. 2
D. 3
-
Câu 35:
Tìm số cực trị của hàm số \(y=x^{4}-2 x^{2}+2\)
A. 1
B. 2
C. 3
D. 4
-
Câu 36:
Tìm giá trị cực đại của hàm số \(y=x^{4}-2 x^{2}+2\)
A. 0
B. 2
C. -1
D. 1
-
Câu 37:
Điểm cực đại của hàm số \(y=x^{4}-2 x^{2}+2\) là:
A. x=1
B. x=2
C. x=3
D. x=0
-
Câu 38:
Điểm cực tiểu của hàm số \(y=-x^{3}+3 x^{2}-3 x+2\) là
A. x=-1
B. x=0
C. x=1
D. Hàm số không có điểm cực tiểu
-
Câu 39:
Điểm cực trị của hàm số \(y=-x^{3}+3 x^{2}-4\) là
A. \(x_{CĐ}=2, x_{CT}=0\)
B. \(x_{CĐ}=-2, x_{CT}=0\)
C. \(x_{CĐ}=0, x_{CT}=2\)
D. \(x_{CĐ}=0, x_{CT}=-2\)
-
Câu 40:
Số cực trị của hàm số \(y=2 x^{3}-6 x+2\) là
A. 1
B. 2
C. 3
D. 4
-
Câu 41:
Cho hàm số y = f(x) xác định trên R và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình 2|f(x)| - m = 0 có đúng bốn nghiệm phân biệt.
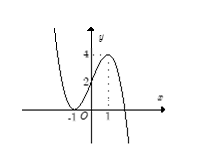
A. 0 < m < 8
B. m > 4
C. m < 0, m > 8
D. - 2 < m < 4
-
Câu 42:
Cho hàm số y = f(x )= ax3+ bx2+ cx+ d có bảng biến thiên như sau:
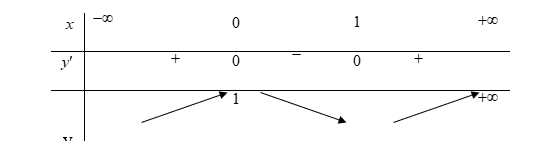
Khi đó |f(x)| = m có 4 nghiệm phân biệt \({x_1} < {x_2} < {x_3} < \frac{1}{2} < {x_4}\) khi và chỉ khi
A. \(\frac{1}{2} < m < 1\)
B. m > 0
C. m > 1
D. \(m < \frac{1}{2} \)
-
Câu 43:
Cho hàm số y = f( x) và đồ thị hình bên là đồ thị của hàm y = f’ (x) . Hỏi đồ thị của hàm số \(g\left( x \right) = \left| {2f\left( x \right) - {{\left( {x - 1} \right)}^2}} \right|\) có tối đa bao nhiêu điểm cực trị ?
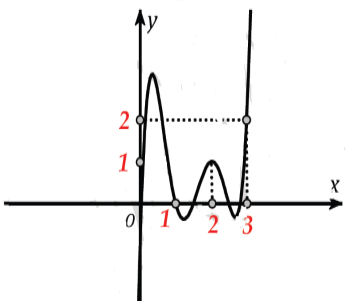
A. 6
B. 7
C. 8
D. 9
-
Câu 44:
Cho hàm số y = f( x) liên tục trên R. Hàm số y = f’ (x) có đồ thị như hình vẽ. Hàm số \(y = g\left( x \right) = f\left( x \right) + \frac{{2017 - 2018x}}{{2017}}\) có bao nhiêu cực trị?
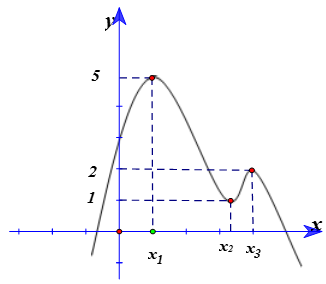
A. 1
B. 2
C. 3
D. 4
-
Câu 45:
Cho hàm số y = x4-2mx2+2 với m là tham số thực. Có bao nhiêu giá trị nguyên của m để đồ thị hàm số có ba điểm cực trị A; B; C thỏa mãn OA.OB.OC = 12?
A. 2
B. 1
C. 0
D. 4
-
Câu 46:
Cho hàm số y = x4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất.
A. \(m = -\frac{1}{2}\)
B. \(m = \frac{1}{2}\)
C. m = 2
D. m = 1
-
Câu 47:
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3-3mx2+2 có hai điểm cực trị A: B sao cho A: B và M( 1; -2) thẳng hàng.
A. m = 0
B. \(m = \sqrt 2 \)
C. \(m = -\sqrt 2 \)
D. Đáp án khác
-
Câu 48:
Cho hàm số y = x3- 3mx2+4m2-2 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có hai điểm cực trị A; B sao cho I( 1; 0) là trung điểm của đoạn thẳng AB.
A. 0
B. - 1
C. 1
D. 2
-
Câu 49:
Cho hàm số y = 2x3+mx2-12x-13 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có hai điểm cực trị cách đều trục tung.
A. m = 2
B. m = - 1
C. m = 1
D. m = 0
-
Câu 50:
Tìm tất cả các giá trị thực của tham số m để hàm số y = x3-3x2+3mx+1 có các điểm cực trị nhỏ hơn 2
A. m < - 1
B. m < 1
C. m > 0
D. 0 < m < 1














