Trắc nghiệm Sự đồng biến, nghịch biến của hàm số Toán Lớp 12
-
Câu 1:
Số các giá trị nguyên của m để hàm số nghịch biến trên khoảng (0;1) là
A. 0
B. 1
C. 2
D. 3
-
Câu 2:
Tổng các giá trị nguyên của để hàm số đồng biến trên khoảng là
A. 134
B. 217
C. 111
D. 325
-
Câu 3:
Tìm các giá trị của m để hàm số đồng biến trên khoảng là?
A.
B.
C.
D.
-
Câu 4:
Số các giá trị nguyên của để hàm số đồng biến trên khoảng là:
A. 15
B. 20
C. 25
D. 30
-
Câu 5:
Cho hàm số với m là tham số thực. Tìm tất cả các giá trị của m để hàm số nghịch biến trên mỗi khoảng xác định.
A.
B.
C.
D.
-
Câu 6:
Cho hàm số với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của để hàm số nghịch biến trên mỗi khoảng xác định.
A. 0
B. 1
C. 2018
D. 2019
-
Câu 7:
Cho hàm số với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên
của m để hàm số nghịch biến trên khoảng . Tìm S .A.
B.
C.
D.
-
Câu 8:
Cho hàm số . Tìm giá trị nguyên của m để hàm số nghịch biến trên khoảng
A. m=0
B. m=1
C. m=2
D. m=3
-
Câu 9:
Cho hàm số . Có bao nhiêu giá trị nguyên m để hàm số nghịch biến trên khoảng
A. 0
B. 1
C. 2
D. 3
-
Câu 10:
Cho hàm số . Tập hợp các giá trị nguyên m để hàm số đồng biến trên khoảng là?
A. m>0
B. m<0
C. m>1
D. m<1
-
Câu 11:
Cho hàm số . Có bao nhiêu giá trị nguyên m thuộc khoảng để hàm số đồng biến trên khoảng
A. 2019
B. 2020
C. 2021
D. 2022
-
Câu 12:
Gọi S là tập hợp các giá trị nào của tham số m để hàm số nghịch biến trên khoảng . Khi đó S là tập con của tập nào sau đây?
A.
B.
C.
D.
-
Câu 13:
Tìm các giá trị của m để hàm số đồng biến trên
A. m>1
B. m>2
C. 1<m<2
D. m<1
-
Câu 14:
Có bao nhiêu số tự nhiên m không vượt quá 2020 và là số chẵn để hàm số đồng biến trên
A. 1000
B. 1010
C. 1004
D. 1400
-
Câu 15:
Tìm tham số m để hàm số nghịch biến trên khoảng ?
A.
B.
C.
D.
-
Câu 16:
Tổng của các giá trị nguyên của tham số m để hàm số đồng biến trên khoảng là?
A. 13
B. 4
C. 3
D. 14
-
Câu 17:
Có bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên khoảng ?
A. 1
B. 2
C. 3
D. 4
-
Câu 18:
Với giá trị của tham số m để hàm số đồng biến trên khoảng
A.
B.
C.
D.
-
Câu 19:
Với giá trị nào của tham số m thì hàm số nghịch biến trên
A.
B.
C.
D.
-
Câu 20:
Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên
A. 3
B. 4
C. 5
D. 6
-
Câu 21:
Tìm các giá trị của tham số m sao cho hàm số nghịch biến trên khoảng
A.
B.
C.
D.
-
Câu 22:
Có bao nhiêu giá trị nguyên của tham số m thuộc (-2020;2020) để hàm số đồng biến trên .
A. 2019
B. 2020
C. 2021
D. 2022
-
Câu 23:
Tính các giá trị của tham số m để hàm số đồng biến trên khoảng .
A.
B.
C.
D. Không tìm được giá trị m.
-
Câu 24:
Tính tổng các giá trị nguyên của tham số m trên khoảng (-2020; 2020 ) để hàm số đồng biến trên khoảng .
A. -2039187
B. 2022 .
C. 2093193 .
D. 2021 .
-
Câu 25:
Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên .
A. 3
B. 5
C. 7
D. 9
-
Câu 26:
Tìm tất cả các giá trị của m để hàm số đồng biến trên .
A.
B.
C.
D.
-
Câu 27:
Gọi là tập hợp các số nguyên để hàm số đồng biến trên khoảng . Tính tổng T của các phần tử trong S ?
A. -7
B. -8
C. -9
D. -10
-
Câu 28:
Tìm tất cả giá trị m để hàm số nghịch biến trên .
A.
B.
C.
D. Không tồn tại giá trị của m.
-
Câu 29:
Số giá trị nguyên thuộc [-5;5] của tham số m sao cho hàm số nghịch biến trên
khoảng làA. 6
B. 7
C. 5
D. 8
-
Câu 30:
Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng
A. 3
B. 4
C. 5
D. 6
-
Câu 31:
Tìm tập hợp tất cả các giá trị của m để hàm số nghịch biến trên khoảng
A.
B.
C.
D.
-
Câu 32:
Cho hàm số y=f(x). Biết hàm số y=f(x) có đồ thị như hình vẽ bên dưới. Hàm số đồng biến trên khoảng
A. (-2;-1)
B. (-1;0)
C. (1;2)
D. (0;1)
-
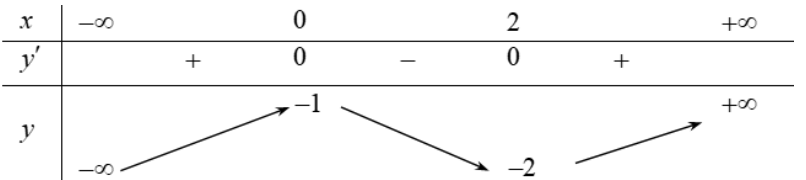
Câu 33:
Cho hàm số y=f(x) liên tục trên và có bảng biến thiên như sau
Hàm số đồng biến trên
A.
B.
C.
D.
-
Câu 34:
Hàm số đồng biến trên khoảng nào dưới đây? A.
B.
C.
D.
-
Câu 35:
Một cửa hàng nhận làm những chiếc xô bằng nhôm hình trụ không có nắp đủ chứa được10 lít nước. Hỏi bán kính đáy (đơn vị cm, làm tròn đến hàng phần chục) của chiếc xô bằng bao nhiêu để cửa hàng tốn ít nguyên vật liệu nhất
A. 14,7
B. 15
C. 15,2
D. 14
-
Câu 36:
Công ty dụ lịch Ban Mê dự định tổ chức một tua xuyên Việt. Công ty dự định nếu giá tua là 2 triệu đồng thì sẽ có khoảng 150 người tham gia. Để kích thích mọi người tham gia, công ty quyết định giảm giá và cứ mỗi lần giảm giá tua 100 ngàn đồng thì sẽ có thêm 20 người tham gia. Hỏi công ty phải bán giá tua là bao nhiêu để doanh thu từ tua xuyên Việt là lớn nhất
A. 1375000.
B. 3781250.
C. 2500000.
D. 3000000.
-
Câu 37:
Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 ngàn đồng một ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 ngàn đồng thì có thêm 2 phòng trống. Giám đốc phải chọn giá phòng mới là bao nhiêu để thu nhập của khách sạn trong ngày là lớn nhất.
A. 480 ngàn
B. 50 ngàn.
C. 450 ngàn.
D. 80 ngàn.
-
Câu 38:
Một đại lý xăng dầu cần xây một bồn chứa dầu hình trụ có đáy hình tròn bằng thép có thể tích và giá mỗi mét vuông thép là 500 ngàn đồng. Hỏi giá tiền thấp nhất mà đại lý phải trả gần đúng với số tiền nào nhất.
A. 79,5 triệu
B. 80,5 triệu
C. 77,4 triệu
D. 75 triệu
-
Câu 39:
Khi xây dựng nhà, chủ nhà cần làm một bể nước bằng gạch có dạng hình hộp có đáy là hình chữ nhật chiều dài d(m) và chiều rộng r (m) với d=2r . Chiều cao bể nước là h(m) và thể tích bể là 2m3 Hỏi chiều cao bể nước như thế nào thì chi phí xây dựng là thấp nhất?
A.
B.
C.
D.
-
Câu 40:
Khi sản xuất vỏ lon sữa bò hình trụ các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích của khối trụ đó bằng 2 và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy gần số nào nhất?
A. 0,68
B. 0,6
C. 90,12
D. 0,52
-
Câu 41:
Trong tất cả các hình chữ nhật có cùng diện tích S, hình chữ nhật có chu vi nhỏ nhất bằng bao nhiêu?
A.
B.
C.
D.
-
Câu 42:
Để giảm nhiệt độ trong phòng từ 280C , một hệ thống làm mát được phép hoạt động trong 10 phút. Gọi T (đơn vị 0C ) là nhiệt độ phòng ở phút thứ t được cho bởi công thức . Tìm nhiệt độ thấp nhất trong phòng đạt được trong\ thời gian 10 phút kể từ khi hệ thống làm mát bắt đầu hoạt động.
A.
B.
C.
D.
-
Câu 43:
Công suất P (đơn vị W ) của một mạch điện được cung cấp bởi một nguồn pin 12V được cho bởi công thức với I (đơn vị A ) là cường độ dòng điện. Tìm công suất tối đa của mạch điện
A. 72
B. 12
C.
D.
-
Câu 44:
Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất.
A.
B.
C.
D.
-
Câu 45:
Một tấm kẽm hình vuông ABCD có cạnh bằng 30(cm). Người ta gập tấm kẽm theo hai cạnh EF và GH cho đến khi AD và BC trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết hai đáy.
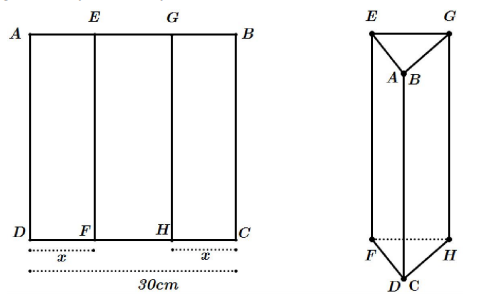
Giá trị của x để thể tích khối lăng trụ lớn nhất là
A.
B.
C.
D.
-
Câu 46:
Trong các hình trụ nội tiếp hình cầu bán kính R, hãy tìm hình trụ có thể tích lớn nhất.
A.
B.
C.
D.
-
Câu 47:
Cho hàm hàm số y =f(x) có bảng biến thiên như hình vẽ dưới
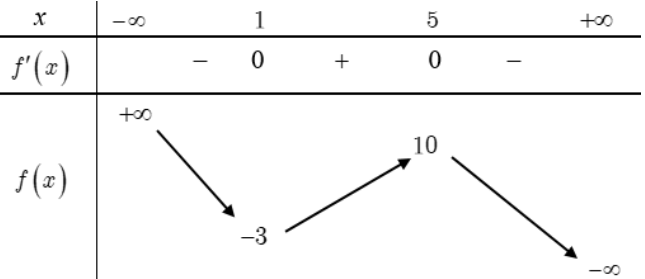
Có bao nhiêu giá trị nguyên của tham số m để phương trình có 6 nghiệm phân biệt
A. 12
B. 27
C. 139
D. 6
-
Câu 48:
Cho hàm số y=f(x) liên tục trên và có đồ thị như hình vẽ.
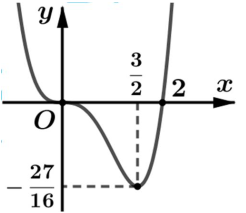
Có bao nhiêu giá trị nguyên của tham số m để phương trình có đúng 12 nghiệm phân biệt thuộc đoạnA. 3
B. 4
C. 2
D. 5
-
Câu 49:
Cho hàm số y =f(x)là một hàm bậc ba có bảng biến thiên
.png)
Có bao nhiêu giá trị nguyên của tham số m để phương trình có đúng ba nghiệm phân biệt?A. 3
B. Vô số
C. 1
D. 2
-
Câu 50:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây.
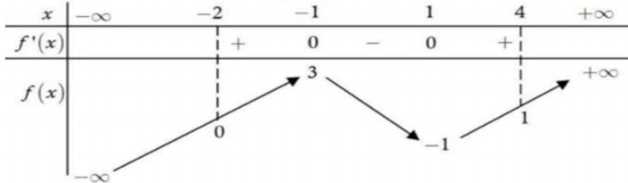
Hỏi có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm trên đoạnA. 8
B. 9
C. 7
D. 6



.PNG)