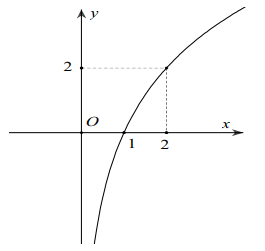Trắc nghiệm Hàm số mũ. Hàm số lôgarit Toán Lớp 12
-
Câu 1:
Cho hàm số \(y=e x+e^{-x}\) . Nghiệm của phương trình y'=0 ?
A. x=0
B. x=1
C. x=-1
D. x=2
-
Câu 2:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\ln \left(x^{2}-2 m x+4\right)\) có tập xác định D=R ?
A. -2<m<2
B. \(\left[\begin{array}{l}m>2 \\ m<-2\end{array}\right.\)
C. \(m>-2\)
D. \(-2 \leq m \leq 2\)
-
Câu 3:
Tính đạo hàm của hàm số \(y=\left(x^{2}+2 x\right) e^{-x} ?\)
A. \(y^{\prime}=(2 x-2) e^{x}\)
B. \(y^{\prime}=\left(x^{2}+2\right) e^{-x}\)
C. \(y^{\prime}=x e^{-x}\)
D. \(y^{\prime}=\left(-x^{2}+2\right) e^{-x}\)
-
Câu 4:
Tìm tập xác định D của hàm số \(y=\sqrt{\log _{3}(x-2)-3} ?\)
A. \(D=[29 ;+\infty)\)
B. \(D=(29 ;+\infty)\)
C. \(D=(2 ; 29)\)
D. \(D=(2 ;+\infty)\)
-
Câu 5:
Tìm tập xác định Dcủa hàm số \(y=\log _{3} \frac{10-x}{x^{2}-3 x+2}\) là?
A. \(\begin{array}{ll} D=(2 ; 10) \end{array}\)
B. \(D=(1 ;+\infty)\)
C. \(D=(-\infty ; 10) \)
D. \(D=(-\infty ; 1) \cup(2 ; 10)\)
-
Câu 6:
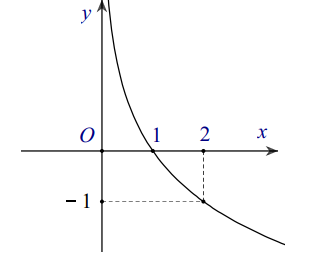
Tìm a để hàm số \(y=\log _{a} x(0 có đồ thị là hình bên dưới:
A. \(a=\frac{1}{2} \)
B. \( a=2 \)
C. \(a=\sqrt{2} \)
D. \(a=\frac{1}{\sqrt{2}}\)
-
Câu 7:
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A. \(y=\log _{2} x \)
B. \( y=\log _{0,5} x\)
C. \( y=-\frac{1}{3} x-\frac{1}{3}\)
D. \( y=-3 x+1\)
-
Câu 8:
Cho hàm số \(f(x)=e^{2017 x^{2}}\) . Đạo hàm f'(0) bằng
A. 0
B. 1
C. e
D. \(e^{2021}\)
-
Câu 9:
Cho hàm số \(f(x)=\ln \left(x^{4}+1\right)\). Đạo hàm f'(0) bằng:
A. 3
B. 2
C. 1
D. 0
-
Câu 10:
Đạo hàm của hàm số \(y=\sin x+\log _{3} x^{3}(x>0)\) là?
A. \(\begin{array}{l} y^{\prime}=-\cos x+\frac{3}{x \ln 3} \end{array}\)
B. \( y^{\prime}=\cos x+\frac{3}{x \ln 3}\)
C. \(y^{\prime}=\cos x+\frac{1}{x^{3} \ln 3}\)
D. \(y^{\prime}=-\cos x+\frac{1}{x^{3} \ln 3}\)
-
Câu 11:
Hàm số \(y=\log _{0,5} x^{2}(x \neq 0)\) có công thức đạo hàm là:
A. \(y^{\prime}=\frac{1}{x^{2} \ln 0,5} \)
B. \(y^{\prime}=\frac{2}{x \ln 0,5} \)
C. \( y^{\prime}=\frac{2}{x^{2} \ln 0,5}\)
D. \(\frac{1}{x \ln 0,5}\)
-
Câu 12:
Đạo hàm của hàm số \(y=\log _{5} x, (x>0)\) là:
A. \(y^{\prime}=5^{x} \ln 5\)
B. \( y^{\prime}=x \ln 5\)
C. \( y^{\prime}=\frac{1}{x \ln 5}\)
D. \( y^{\prime}=\frac{1}{5^{x} \ln 5}\)
-
Câu 13:
Đạo hàm của hàm số \(y=4^{2 x}\) là:
A. \(y^{\prime}=2 \cdot 4^{2 x} \ln 4 \)
B. \(y^{\prime}=4^{2 x} \cdot \ln 2 \)
C. \( y^{\prime}=4^{2 x} \ln 4\)
D. \(y^{\prime}=2.4^{2 x} \ln 2\)
-
Câu 14:
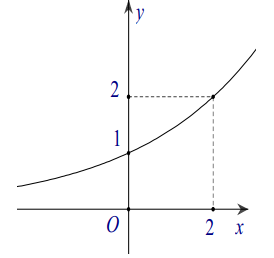
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A. \(y=(\sqrt{2})^{-x}\)
B. \(y=x \quad \)
C. \( y=2^{x} \)
D. \( y=(\sqrt{2})^{x}\)
-
Câu 15:
Hàm số \(y=\log _{x-1} x\) xác định khi và chỉ khi :
A. x>0
B. x>1
C. \(\begin{array}{l} \left\{\begin{array}{l} x>1 \\ x \neq 2 \end{array}\right. \end{array}\)
D. \(x \neq 2\)
-
Câu 16:
Tập xác định của hàm số \(y=\ln (\ln x)\) là :
A. \(D=(0 ;+\infty)\)
B. \(D=(1 ;+\infty)\)
C. \(D=(e ;+\infty)\)
D. \(D=[1 ;+\infty)\)
-
Câu 17:
Tập xác định \(y=\sqrt{-2 x^{2}+5 x-2}+\ln \frac{1}{x^{2}-1}\) là?
A. D=(1 ; 2]
B. D=[1 ; 2]
C. D=(-1 ; 1)
D. D=(-1 ; 2)
-
Câu 18:
Tập xác định của hàm số \(y=\frac{e^{x}}{e^{x}-1}\) là?
A. \(\begin{array}{llll} D=(e ;+\infty) \end{array}\)
B. \((0 ;+\infty)\)
C. \(\mathbb{R} \backslash\{1\} \)
D. \(D=\mathbb{R} \backslash\{0\}\)
-
Câu 19:
Tập xác định của hàm số \(y=\frac{1}{\sqrt{2-x}}+\ln (x-1)\) là?
A. \(D=[1 ; 2]\)
B. \(D=(1 ;+\infty)\)
C. \(D=(0 ;+\infty)\)
D. \(D=(1 ; 2)\)
-
Câu 20:
Tập xác định của hàm số \(y=\log _{2} \frac{x+3}{2-x}\) là?
A. \(D=\mathbb{R} \backslash\{-3 ; 2\}\)
B. \( D=(-3 ; 2)\)
C. \(D=(-\infty ;-3) \cup(2 ;+\infty)\)
D. \(D=[-3 ; 2]\)
-
Câu 21:
Tìm x để hàm số \(y=\log \sqrt{x^{2}+2x-15}\) có nghĩa.
A. \(\begin{array}{l} x \neq-5 \end{array}\)
B. \(x \in(-5 ; 3)\)
C. \(x \in(-\infty ;-5) \cup(3 ;+\infty)\)
D. \(x \in R\)
-
Câu 22:
Tính giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } \left( {x{e^{{1 \over x}}} - x} \right)\)
A. 0
B. 1
C. -1
D. 3
-
Câu 23:
Tính giới hạn: \(\mathop {\lim }\limits_{x \to 5} \left( {{2^x} - {3^x}} \right)\)
A. -210
B. -211
C. -212
D. -213
-
Câu 24:
Tìm giới hạn: \(\mathop {\lim }\limits_{x \to 0} {{{e^{2x}} - {e^{3x}}} \over {5x}}\)
A. \(- {1 \over 5}\)
B. \(- {2 \over 5}\)
C. \(- {3 \over 5}\)
D. \(- {4 \over 5}\)
-
Câu 25:
Tính giới hạn: \(\mathop {\lim }\limits_{x \to 0} {{{e^{3x}} - 1} \over x}\)
A. 1
B. 2
C. 3
D. 4
-
Câu 26:
Cho hàm số \(\displaystyle y = \frac{{\ln x}}{x}\). Chọn khẳng định đúng:
A. Hàm số có một cực tiểu
B. Hàm số có một cực đại
C. Hàm số không có cực trị
D. Hàm số có một cực đại và một cực tiểu
-
Câu 27:
Đạo hàm của hàm số \(\displaystyle y = x\left( {\ln x - 1} \right)\) là:
A. \(\displaystyle \ln x - 1\)
B. \(\displaystyle \ln x\)
C. \(\displaystyle \frac{1}{x} - 1\)
D. 1
-
Câu 28:
Hàm số \(\displaystyle y = \ln \left( {{x^2} - 2mx + 4} \right)\) có tập xác định \(\displaystyle D = \mathbb{R}\) khi:
A. m = 2
B. m > 2 hoặc m < - 2
C. m < 2
D. - 2 < m < 2
-
Câu 29:
Hàm số \(\displaystyle y = {x^2}{e^{ - x}}\) tăng trong khoảng:
A. \(\displaystyle \left( { - \infty ;0} \right)\)
B. \(\displaystyle \left( {2; + \infty } \right)\)
C. \(\displaystyle \left( {0;2} \right)\)
D. \(\displaystyle \left( { - \infty ; + \infty } \right)\)
-
Câu 30:
Nếu \(\displaystyle {a^{\frac{{\sqrt 3 }}{3}}} > {a^{\frac{{\sqrt 2 }}{2}}}\) và \(\displaystyle {\log _b}\frac{3}{4} < {\log _b}\frac{4}{5}\) thì:
A. \(\displaystyle 0 < a < 1,b > 1\)
B. \(\displaystyle 0 < a < 1,0 < b < 1\)
C. \(\displaystyle a > 1,b > 1\)
D. \(\displaystyle a > 1,0 < b < 1\)
-
Câu 31:
Đạo hàm của hàm số \(\displaystyle y = \frac{{{e^x} - {e^{ - x}}}}{x}\) là:
A. \(\displaystyle \frac{{x({e^x} - {e^{ - x}}) - {e^x} + {e^{ - x}}}}{{{x^2}}}\)
B. \(\displaystyle \frac{{x({e^x} + {e^{ - x}}) - {e^x} + {e^{ - x}}}}{{{x^2}}}\)
C. \(\displaystyle \frac{{x({e^x} + {e^{ - x}}) - {e^x} - {e^{ - x}}}}{{{x^2}}}\)
D. \(\displaystyle \frac{{x({e^x} + {e^{ - x}}) + {e^x} + {e^{ - x}}}}{{{x^2}}}\)
-
Câu 32:
Hàm số \(\displaystyle y = {e^x}\sin x\) có đạo hàm là:
A. \(\displaystyle {e^x}(\sin x + \cos x)\)
B. \(\displaystyle {e^x}(\sin x - \cos x)\)
C. \(\displaystyle {e^x}(\sin x + \cot x)\)
D. \(\displaystyle {e^x}(\sin x - \cot x)\)
-
Câu 33:
Hàm số \(\displaystyle y = \ln (\cos x)\) có đạo hàm là:
A. - cot x
B. tan x
C. -tan x
D. cot x
-
Câu 34:
Hàm số \(\displaystyle y = (3{x^2} - 2){\log _2}x\) có đạo hàm là:
A. \(\displaystyle 5x{\log _2}x + \frac{{3{x^2} - 2}}{{x\ln 2}}\)
B. \(\displaystyle 6x{\log _2}x + \frac{{3{x^2} - 2}}{{x\ln 2}}\)
C. \(\displaystyle 7x{\log _2}x + \frac{{3{x^2} - 2}}{{x\ln 2}}\)
D. \(\displaystyle 8x{\log _2}x + \frac{{3{x^2} - 2}}{{x\ln 2}}\)
-
Câu 35:
Hàm số \(\displaystyle y = 3{x^{ - 3}} - {\log _3}x\) có đạo hàm là:
A. \(\displaystyle 9{x^{ - 4}}+ \frac{1}{{x\ln 3}}\)
B. \(\displaystyle - 9{x^{ - 4}} + \frac{1}{{x\ln 3}}\)
C. \(\displaystyle - 9{x^{ - 4}} - \frac{1}{{x\ln 3}}\)
D. \(\displaystyle 9{x^{ - 4}} - \frac{1}{{x\ln 3}}\)
-
Câu 36:
TXĐ của hàm số \(\displaystyle y = \sqrt {\log (x - 1) + \log (x + 1)} \) là:
A. \(\displaystyle D = \left[ {\sqrt 6 ; + \infty } \right)\).
B. \(\displaystyle D = \left[ {\sqrt 5 ; + \infty } \right)\).
C. \(\displaystyle D = \left[ {\sqrt 3 ; + \infty } \right)\).
D. \(\displaystyle D = \left[ {\sqrt 2 ; + \infty } \right)\).
-
Câu 37:
TXĐ của hàm số \(\displaystyle y = \sqrt {\log x + \log (x + 2)} \) là:
A. \(\displaystyle D = \left[ { 1 + \sqrt 2 ; + \infty } \right)\).
B. \(\displaystyle D = \left[ { - 1 + \sqrt 2 ; + \infty } \right)\).
C. \(\displaystyle D = \left[ { - 1 - \sqrt 2 ; + \infty } \right)\).
D. \(\displaystyle D = \left[ { 1 - \sqrt 2 ; + \infty } \right)\).
-
Câu 38:
TXĐ của hàm số \(\displaystyle y = {\log _6}\frac{{3x + 2}}{{1 - x}}\) là:
A. \(\displaystyle D = \left( { - \frac{2}{3};1} \right)\).
B. \(\displaystyle D = \left( { - \frac{2}{3};2} \right)\).
C. \(\displaystyle D = \left( { - \frac{2}{3};3} \right)\).
D. \(\displaystyle D = \left( { - \frac{2}{3};4} \right)\).
-
Câu 39:
TXĐ D của hàm số \(\displaystyle y = \frac{2}{{\sqrt {{4^x} - 2} }}\) là:
A. \(\displaystyle D = \left( {\frac{1}{2}; + \infty } \right)\)
B. \(\displaystyle D = \left( {\frac{1}{3}; + \infty } \right)\)
C. \(\displaystyle D = \left( {\frac{1}{4}; + \infty } \right)\)
D. \(\displaystyle D = \left( {\frac{1}{5}; + \infty } \right)\)
-
Câu 40:
Trong các hàm số sau đây, hàm số nào nghịch biến?
A. \(\displaystyle y = \lg x\)
B. \(\displaystyle y = \ln x\)
C. \(\displaystyle y = {\log _{\sqrt 3 }}x\)
D. \(\displaystyle y = {\log _{\frac {2}{e}}}x\)
-
Câu 41:
Trong các hàm số sau đây, hàm số nào đồng biến?
A. \(\displaystyle y = {\log _{\frac {1}{e}}}x\)
B. \(\displaystyle y = {\log _{\frac {\pi }{3}}}x\)
C. \(\displaystyle y = {\log _{\frac {{\sqrt 2 }}{2}}}x\)
D. \(\displaystyle y = {\log _{\frac {e}{3}}}x\)
-
Câu 42:
Tìm \(\displaystyle x\), biết \(\displaystyle {\left( {\sqrt 3 - \sqrt 2 } \right)^x} = \sqrt 3 + \sqrt 2 \).
A. x = 1
B. x = 2
C. \(\displaystyle x = \frac {1}{2}\)
D. x = - 1
-
Câu 43:
Tìm \(\displaystyle x\), biết \(\displaystyle {9^x} = \frac {1}{3}\).
A. x = - 2
B. x = 2
C. \(\displaystyle x = \frac {1}{2}\)
D. \(\displaystyle x = - \frac {1}{2}\)
-
Câu 44:
Tìm \(\displaystyle x\), biết \(\displaystyle {\left( {\frac {1}{4}} \right)^x} = 16\).
A. x = - 2
B. x = 2
C. \(\displaystyle x = \frac {1}{2}\)
D. \(\displaystyle x = - \frac {1}{2}\)
-
Câu 45:
Tìm \(\displaystyle x\), biết \(\displaystyle {3^x} = \frac {1}{{81}}\).
A. x = 4
B. x = - 4
C. x = 3
D. x = - 3
-
Câu 46:
Tìm \(\displaystyle x\), biết \(\displaystyle {2^x} = 64\).
A. x = 4
B. x = 5
C. x = 6
D. x = 8
-
Câu 47:
Với giá trị nào của \(\displaystyle x\) thì đồ thị hàm số \(\displaystyle y = {\left( {\frac {2}{3}} \right)^x}\) nằm phía trên đường thẳng \(\displaystyle y = 1\)?
A. x > 0
B. x < 0
C. x < 0
D. x < 1
-
Câu 48:
Với giá trị nào của \(\displaystyle x\) thì đồ thị hàm số \(\displaystyle y = {4^x}\) nằm phía trên đường thẳng \(\displaystyle y = 1\)?
A. x > 0
B. x < 0
C. x = 0
D. x < 1
-
Câu 49:
Trong các hàm số sau, hàm số nào nghịch biến?
A. \(\displaystyle y = {\left( {\frac {2}{{\sqrt 3 }}} \right)^x}\)
B. \(\displaystyle y = {\left( {\frac {3}{\pi }} \right)^x}\)
C. \(\displaystyle y = {\pi ^x}\)
D. \(\displaystyle y = {\left( {\frac {{\sqrt 5 }}{2}} \right)^x}\)
-
Câu 50:
Trong các hàm số sau, hàm số nào đồng biến?
A. \(\displaystyle y = {\left( {\frac {{\sqrt 3 }}{2}} \right)^x}\)
B. \(\displaystyle y = {\left( {\frac {e}{3}} \right)^x}\)
C. \(\displaystyle y = {\left( {\frac {\pi }{4}} \right)^x}\)
D. \(\displaystyle y = {\left( {\frac {3}{e}} \right)^x}\)