Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Lương Văn Can
-
Câu 1:
Có bao nhiêu cách chọn ra hai học sinh gồm nam và nữ từ nhóm 1010 học sinh gồm 4 nam và 6 nữ?
A. C210.
B. A210.
C. C14+C16.
D. C14⋅C16.
-
Câu 2:
Cho cấp số cộng (un) có số hạng đầu u1=2 và số hạng thứ tư u4=17. Công sai của cấp số cộng đã cho bằng
A. 152.
B. 5.
C. 3.
D. 15.
-
Câu 3:
Nghiệm của phương trình log2(x−1)=4 là
A. x=2.
B. x=15.
C. x=9.
D. x=17.
-
Câu 4:
Tập xác định của hàm số y=(2−x)12là
A. (2;+∞).
B. (−∞;2).
C. (−∞;2].
D. [2;+∞).
-
Câu 5:
Cho khối lăng trụ có diện tích đáy bằng B=3 và chiều cao h=4. Thể tích của khối lăng trụ này bằng
A. 12.
B. 4.
C. 24.
D. 6.
-
Câu 6:
Cho hình trụ có bán kính r=2 và chiều cao h=3. Diện tích xung quanh của hình trụ này bằng
A. 24π.
B. 12π.
C. 6π.
D. 20π.
-
Câu 7:
Cho khối cầu có bán kính R=6. Thể tích khối cầu bằng
A. 144π.
B. 36π.
C. 288π.
D. 48π.
-
Câu 8:
Cho hàm số f(x) liên tục trên R và có bảng biến thiên như sau:
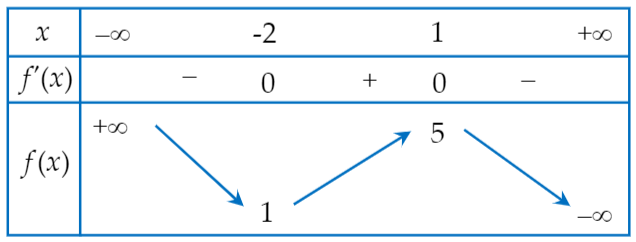
Hàm số f(x) đồng biến trên khoảng nào dưới đây?
A. (−2;+∞).
B. (−∞;−2).
C. (−2;0).
D. (−∞;−1).
-
Câu 9:
Với a,b là các số thực dương tùy ý, log(a5b10) bằng
A. 5loga+10logb.
B. 12loga+logb.
C. 5log(ab).
D. 10log(ab).
-
Câu 10:
Cho hàm số y=f(x) có đạo hàm liên tục trên R và dấu của đạo hàm cho bởi công thức

Hàm số f(x) có mấy điểm cực trị?
A. 3
B. 2
C. 1
D. 5
-
Câu 11:
Đồ thị của hàm số nào sau đây có dạng như đường cong trong hình vẽ bên?
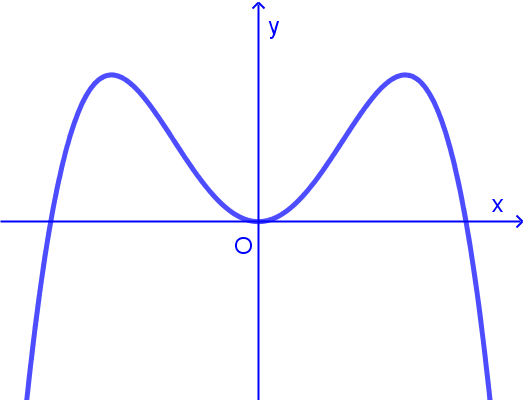
A. y=x3+3x2.
B. y=−x3+3x.
C. y=x4−2x2.
D. y=−x4+2x2.
-
Câu 12:
Đường tiệm cận đứng của đồ thị hàm số y=xx−1, là
A. x=1.
B. x=0.
C. y=1.
D. y=0.
-
Câu 13:
Tập nghiệm của bất phương trình 52x+1≤25 là
A. (−∞;12).
B. (−∞;−12).
C. (−∞;−12].
D. (−∞;12].
-
Câu 14:
Cho hàm số f(x) liên tục trên R và có đồ thị là đường cong như hình vẽ bên dưới.
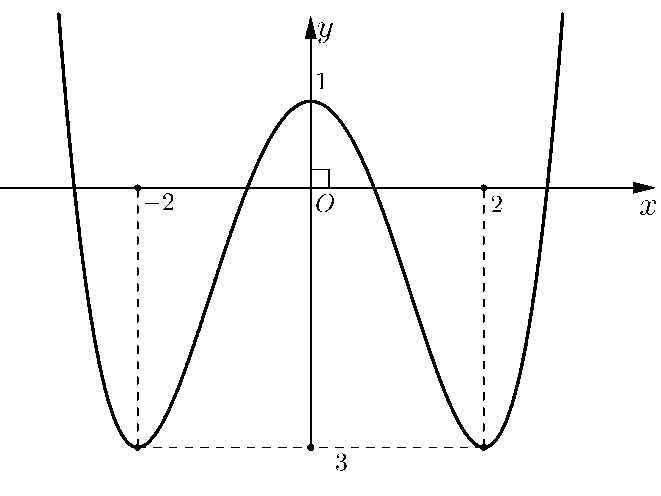
Số nghiệm của phương trình 2f(x)+1=0 là
A. 1
B. 2
C. 3
D. 4
-
Câu 15:
Cho hàm số f(x), g(x) liên tục trên [0;2] và 2∫0f(x)dx=2, 2∫0g(x)dx=−2. Tính 2∫0[3f(x)+g(x)]dx.
A. 4
B. 8
C. 12
D. 6
-
Câu 16:
Cho các số phức z=2+i và ω=3−2i. Phần ảo của số phức z+2ω bằng
A. 8.
B. −3i.
C. −4.
D. −3.
-
Câu 17:
Cho số phức z=2i+1. Điểm nào sau đây là điểm biểu diễn của số phức z trên mặt phẳng tọa độ?
A. H(1;2).
B. G(1;−2).
C. T(2;−1).
D. K(2;1).
-
Câu 18:
Trong không gian Oxyz, hình chiếu vuông góc của điểm M(3;1;2) lên trục Oy là điểm
A. E(3;0;2).
B. F(0;1;0).
C. L(0;−1;0).
D. S(−3;0;−2).
-
Câu 19:
Trong không gian Oxyz, cho mặt cầu (S):x2+y2+z2−2x+4y+1=0. Tính diện tích của mặt cầu (S)
A. 4π.
B. 64π.
C. 32π3.
D. 16π.
-
Câu 20:
Trong không gian Oxyz, cho mặt phẳng (P):2x+y−z+3=0. Điểm nào sau đây không thuộc mặt phẳng (P)?
A. V(0;−2;1).
B. Q(2;−3;4).
C. T(1;−1;1).
D. I(5;−7;6).
-
Câu 21:
Cho số phức z=2+i. Mô đun của số phức w=¯z+3z bằng
A. 2√17.
B. √17.
C. 17.
D. 68.
-
Câu 22:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA=1 và đáy ABC là tam giác đều với độ dài cạnh bằng 2. Tính góc giữa mặt phẳng (SBC) và mặt phẳng (ABC).
A. 600.
B. 450.
C. 300.
D. 900.
-
Câu 23:
Cho hàm số f(x) thỏa mãn f′(x)=x2(x−1),∀x∈R. Phát biểu nào sau đây là đúng?
A. f(x) có hai điểm cực trị.
B. f(x) không có cực trị.
C. f(x) đạt cực tiểu tại x=1.
D. f(x) đạt cực tiểu tại x=0.
-
Câu 24:
Giá trị lớn nhất của hàm số y=x2−2x+1x+2 trên đoạn [0;3] bằng
A. 0.
B. 12.
C. 32.
D. 45.
-
Câu 25:
Biết rằng log34=a và T=log1218. Phát biểu nào sau đây là đúng?
A. T=a+22a+2.
B. T=a+42a+2.
C. T=√a+2a+1.
D. T=√a−2a+1.
-
Câu 26:
Tập nghiệm của bất phương trình log22(2x)+1≤log2(x5)là
A. (0;4].
B. (0;2].
C. [2;4].
D. [1;4].
-
Câu 27:
Xét tích phân I=∫10e√2x+1dx, nếu đặt u=√2x+1thì I bằng
A. 12∫21ueudu.
B. ∫40ueudu.
C. ∫31ueudu.
D. 12∫31eudu
-
Câu 28:
Gọi (H) là hình phẳng giới hạn bởi các đồ thị y=x2−2x, y=0 trong mặt phẳng Oxy. Quay hình (H) quanh trục hoành ta được một khối tròn xoay có thể tích bằng
A. 2∫0|x2−2x|dx.
B. π2∫0|x2−2x|dx.
C. π2∫0(x2−2x)2dx.
D. 2∫0(x2−2x)2dx.
-
Câu 29:
Cho z1, z2 là các nghiệm phức phân biệt của phương trình z2−4z+13=0. Tính |z1+i|2+|z2+i|2.
A. 28.
B. 2√5+2√2.
C. 36.
D. 6√2.
-
Câu 30:
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng 3a.
Khoảng cách từ A đến mặt phẳng (SCD) bằng
A. a√143.
B. a√144.
C. a√14.
D. a√142.
-
Câu 31:
Trong không gian Oxyz, cho A(1;1;−2); B(2;0;3); C(−2;4;1). Mặt phẳng đi qua A và vuông góc với đường thẳng BC có phương trình là
A. x+y−2z−6=0.
B. 2x−2y+z+2=0.
C. 2x+2y+z−2=0.
D. x+y−2z+2=0.
-
Câu 32:
Trong không gian Oxyz, cho điểm A(1;1;−2) và đường thẳng d:x−12=y+11=z−2. Đường thẳng qua A và song song với d có phương trình tham số là
A. {x=1+2ty=1−tz=−2−2t.
B. {x=1+2ty=1+tz=−2−2t.
C. {x=1+2ty=1+tz=2−2t.
D. {x=1+ty=1+tz=−2−2t.
-
Câu 33:
Cho hàm số y=x3−3mx2+12x+3m−7 với m là tham số. Số các giá trị nguyên của m đề hàm số đã cho đồng biến trên R là
A. 4
B. 3
C. 5
D. 6
-
Câu 34:
Tập xác định của hàm số y=√log12(x2+7x)+3 là
A. [−8;−7)∪(0;1).
B. [−8;−7]∪(0;1].
C. (−8;−7)∪(0;1).
D. [−8;−7)∪(0;1].
-
Câu 35:
Có bao nhiêu số phức z thỏa mãn (z2−2z+7)(z−2¯z2)=0?
A. 3
B. 5
C. 6
D. 4
-
Câu 36:
Có 6 học sinh gồm 2 học sinh lớp A, 2 học sinh lớp B và 2 học sinh lớp C xếp ngẫu nhiên thành một hàng ngang. Tính xác suất để nhóm bất kì 3 học sinh liền kề nhau trong hàng luôn có mặt học sinh của 3 lớp A, B, C.
A. 1120.
B. 13.
C. 130.
D. 115.
-
Câu 37:
Cho hình trụ có bán kính đáy bằng a√3. Cắt hình trụ bởi một mặt phẳng song song với trục, cách trục một khoảng bằng a ta được thiết diện là một hình vuông. Thể tích khối trụ đó bằng
A. 2πa3√2.
B. 4πa3√2.
C. 6πa3√2.
D. 3πa3√2.
-
Câu 38:
Cho hình tứ diện đều ABCD có cạnh bằng a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách giữa hai đường thẳng AB và CM theo a.
A. a√3311.
B. a√33.
C. a√22.
D. a√2211.
-
Câu 39:
Biết rằng đồ thị (H):y=x2+2x+mx−2 có hai điểm cực trị A,B. Hãy tính khoảng cách từ gốc tọa độ đến đường thẳng AB
A. 2√5.
B. √55.
C. 3√5.
D. 1√5.
-
Câu 40:
Cho hàm số f(x) thỏa mãn f(0)=23 và (√x+√x+1).f′(x)=1,∀x≥−1. Biết 1∫0f(x)dx=a√2+b15 với a,b∈Z. Tính T=a+b
A. −8.
B. −24.
C. 24.
D. 8.
-
Câu 41:
Cho hàm số
f(x)={3x2ln(x+1) khi x≥02x√x2+3+1 khi x<0.
Biết e∫1ef(lnx)xdx=a√3+bln2+c với a,b,c∈Q. Giá trị của a+b+6c bằng
A. 35.
B. −14.
C. −27.
D. 18.
-
Câu 42:
Xét hàm số f(x)=|mx−2√x+42x+4| với m là tham số thực. Có bao nhiêu số nguyên m thỏa mãn điều kiện 0<min[−1;1]f(x)<1?
A. 4
B. 8
C. 2
D. 1
-
Câu 43:
Có bao nhiêu giá trị nguyên của tham số m để phương trình log23x−mlog9x2+2−m=0 có nghiệm x∈[1;9].
A. 1
B. 5
C. 3
D. 2
-
Câu 44:
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có AB=2AC và điểm M(2;0;4). Biết điểm B thuộc đường thẳng d:x1=y1=z1, điểm C thuộc mặt phẳng (P):2x+y−z−2=0 và AM là phân giác trong của tam giác ABC kẻ từ A(M∈BC). Phương trình đường thẳng BC là
A. {x=2−ty=tz=4+t.
B. {x=−2+2ty=−2+tz=−2+3t.
C. {x=2y=2−tz=2+t.
D. {x=2y=tz=4−t.
-
Câu 45:
Cho hàm số y=f(x) liên tục trên R, có đồ thị f′(x) như hình vẽ.
Số điểm cực tiểu của hàm số g(x)=f(−x2+x) là
A. 1.
B. 4.
C. 3.
D. 2.
-
Câu 46:
Trong không gian Oxyz cho mặt cầu (S):(x+2)2+y2+(z+5)2=24 cắt mặt phẳng
(α):x+y+4=0 theo giao tuyến là đường tròn (C). Điểm M thuộc (C) sao cho khoàng cách từ M đến A(4;−12;1) nhỏ nhất có tung độ bằng
A. −6.
B. −4.
C. 0.
D. 2.
-
Câu 47:
Cho khối lăng trụ đứng ABC.A′B′C′ có đáy ABC là tam giác vuông cân tại C, AB=2a và góc tạo bởi hai mặt phẳng (ABC′) và (ABC) bằng 60∘. Gọi M,N lần lượt là trung điểm của A′C′ và BC. Mặt phẳng (AMN) chia khối lăng trụ thành hai phần. Thể tích của phần nhỏ bằng
A. 7√3a324.
B. √6a36.
C. 7√6a324.
D. √3a33.
-
Câu 48:
Cho hàm số bậc bốn y=f(x). Biết hàm số y=f′(1+x) có đồ thị như trong hình bên.
Có bao nhiêu số nguyên dương m sao cho hàm số g(x)=f(−x2+2x−2022+m) đồng biến trên (0;1)?
A. 2023.
B. 2021.
C. 2022.
D. 2024.
-
Câu 49:
Cho số phức z thỏa mãn |z+1|≥1. Gọi giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=|(1+i)z+i+2z+1| lần lượt là M và m. Khi đó giá trị của (M2+m2) bằng:
A. 4.
B. 8+4√3.
-
Câu 50:
Có bao nhiêu bộ (x;y) với x,y nguyên và 1≤x,y≤2020 thỏa mãn
(xy+2x+4y+8)log3(2yy+2)≤(2x+3y−xy−6)log2(2x+1x−3)?
A. 2017.
B. 4034.
C. 2.
D. 2017×2020.



.PNG)
.PNG)
.PNG)
.PNG)











