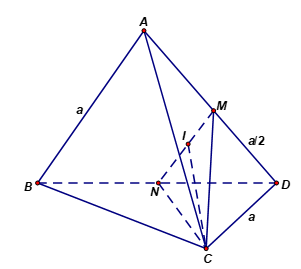
Cho hình tứ diện đều \(ABCD\) có cạnh bằng \(a\). Gọi \(M\) là trung điểm của cạnh \(AD\). Tính khoảng cách giữa hai đường thẳng \(AB\) và \(CM\) theo \(a\).
.PNG)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn D
Gọi \(N\) là trung điểm của \(BD\), \(I\) là trung điểm của \(MN\).
Tam giác \(CMN\) là tam giác cân có \(CM=CN=\frac{a\sqrt{3}}{2};\,\,MN=\frac{a}{2}\)\( \Rightarrow CI=\frac{a\sqrt{11}}{4}\) nên có diện tích \({{S}_{CMN}}=\frac{{{a}^{2}}\sqrt{11}}{16}\).
Thể tích khối tứ diện đều cạnh \(a\) là \(\frac{{{a}^{3}}\sqrt{3}}{12}\).
Vậy thể tích khối tứ diện \(M.NCD\) là \({{V}_{M.NCD}}\)\( =\frac{1}{4}.\frac{{{a}^{3}}\sqrt{3}}{12}\)\( =\frac{{{a}^{3}}\sqrt{3}}{48}\).
Vậy \(d\left( D,\,\left( CMN \right) \right)=d\left( A,\,\left( CMN \right) \right)\)\( =d\left( AB,\,CM \right)\)\( =\frac{3{{V}_{M.CDN}}}{{{S}_{CMN}}}\)\( =\frac{\frac{3.{{a}^{3}}\sqrt{2}}{48}}{\frac{{{a}^{2}}\sqrt{11}}{16}}\)\( =\frac{a\sqrt{22}}{11}\).
Vì khối lập phương \(ABCD.A'B'C'D'\) có thể tích bằng \(8{{a}^{3}}\)\( ={{\left( 2a \right)}^{3}}\) nên cạnh của hình lập phương là \(2a\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Lương Văn Can
Câu hỏi liên quan
-
Với \(a,b\) là các số thực dương tùy ý, \(\log \left( {{a}^{5}}{{b}^{10}} \right)\) bằng
-
Biết rằng \({{\log }_{3}}4=a\) và \(T={{\log }_{12}}18\). Phát biểu nào sau đây là đúng?
-
Có bao nhiêu bộ \(\left( x;y \right)\) với \(x,y\) nguyên và \(1\le x,y\le 2020\) thỏa mãn
\(\left( xy+2x+4y+8 \right){{\log }_{3}}\left( \frac{2y}{y+2} \right)\le \left( 2x+3y-xy-6 \right){{\log }_{2}}\left( \frac{2x+1}{x-3} \right)\)?
-
Cho \({{z}_{1}}\), \({{z}_{2}}\) là các nghiệm phức phân biệt của phương trình \({{z}^{2}}-4z+13=0\). Tính \({{\left| {{z}_{1}}+i \right|}^{2}}+{{\left| {{z}_{2}}+i \right|}^{2}}\).
-
Có 6 học sinh gồm 2 học sinh lớp A, 2 học sinh lớp B và 2 học sinh lớp C xếp ngẫu nhiên thành một hàng ngang. Tính xác suất để nhóm bất kì 3 học sinh liền kề nhau trong hàng luôn có mặt học sinh của 3 lớp A, B, C.
-
Cho hàm số bậc bốn \(y=f\left( x \right)\). Biết hàm số \(y={f}'\left( 1+x \right)\) có đồ thị như trong hình bên.
.PNG)
Có bao nhiêu số nguyên dương \(m\) sao cho hàm số \(g\left( x \right)=f\left( -{{x}^{2}}+2x-2022+m \right)\) đồng biến trên \(\left( 0\,;\,1 \right)\)?
-
Cho hàm số \(y=f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và dấu của đạo hàm cho bởi công thức
Hàm số \(f\left( x \right)\) có mấy điểm cực trị?
-
Cho khối lăng trụ có diện tích đáy bằng \(B=3\) và chiều cao \(h=4\). Thể tích của khối lăng trụ này bằng
-
Tập xác định của hàm số \({y=\sqrt{\log _{\frac{1}{2}}\left(x^{2}+7 x\right)+3}}\) là
-
Nghiệm của phương trình \({{\log }_{2}}\left( x-1 \right)=4\) là
-
Cho khối cầu có bán kính \(R=6\). Thể tích khối cầu bằng
-
Trong không gian \(Oxyz\) cho mặt cầu \((S):(x+2)^{2}+y^{2}+(z+5)^{2}=24\) cắt mặt phẳng
\((\alpha): x+y+4=0\) theo giao tuyến là đường tròn \((C)\). Điểm \(M\) thuộc \((C)\) sao cho khoàng cách từ \(M\) đến \(A(4 ;-12 ; 1)\) nhỏ nhất có tung độ bằng
-
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\), có đồ thị \({f}'\left( x \right)\) như hình vẽ.
.PNG)
Số điểm cực tiểu của hàm số \(g\left( x \right)=f\left( -{{x}^{2}}+x \right)\) là
-
Xét tích phân \(I=\int_{0}^{1}{{{e}^{\sqrt{2x+1}}}\text{d}x}\), nếu đặt \(u=\sqrt{2x+1}\)thì \(I\) bằng
-
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
Hàm số \(f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
-
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(2a\), cạnh bên bằng \(3a\).
.PNG)
Khoảng cách từ \(A\) đến mặt phẳng \(\left( SCD \right)\) bằng
-
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong như hình vẽ bên dưới.
Số nghiệm của phương trình \(2f\left( x \right)+1=0\) là
-
Trong không gian \(Oxyz\), cho \(A\left( 1;1;-2 \right)\); \(B\left( 2;0;3 \right)\); \(C\left( -2;4;1 \right)\). Mặt phẳng đi qua \(A\) và vuông góc với đường thẳng \(BC\) có phương trình là
-
Cho hàm số
\(f\left( x \right)=\left\{ \begin{align} & 3{{x}^{2}}\ln \left( x+1 \right)\text{ khi }x\ge 0 \\ & 2x\sqrt{{{x}^{2}}+3}+1\text{ khi }x<0 \\ \end{align} \right.\).
Biết \(\int\limits_{\frac{1}{e}}^{e}{\frac{f\left( \ln x \right)}{x}dx}=a\sqrt{3}+b\ln 2+c\) với \(a,b,c\in \mathbb{Q}\). Giá trị của \(a+b+6c\) bằng
-
Cho khối lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác vuông cân tại \(C\), \(AB=2a\) và góc tạo bởi hai mặt phẳng \(\left( AB{C}' \right)\) và \(\left( ABC \right)\) bằng \(60{}^\circ \). Gọi \(M,N\) lần lượt là trung điểm của \({A}'{C}'\) và \(BC\). Mặt phẳng \(\left( AMN \right)\) chia khối lăng trụ thành hai phần. Thể tích của phần nhỏ bằng
