Trắc nghiệm Tích phân Toán Lớp 12
-
Câu 1:
Diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số \(y=2 x^{3}-3 x^{2}+1\) và \(y=x^{3}-4 x^{2}+2 x+1\) là:
A. \(\frac{37}{13}\)
B. \(\frac{37}{12}\)
C. 3
D. 4
-
Câu 2:
Diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số \(y=\sqrt{x} \text { và } y=\sqrt[3]{x}\)
A. \(\frac{1}{12}\)
B. \(\frac{1}{13}\)
C. \(\frac{1}{14}\)
D. \(\frac{1}{15}\)
-
Câu 3:
Diện tích hình phẳng giới hạn bởi các đồ thị của các hàm số \(y=x^{2}\,và\,y=x \,là\)
A. \(\frac{\pi}{6}\)
B. \(\frac{1}{6}\)
C. \(\frac{5}{6}\)
D. \(-\frac{1}{6}\)
-
Câu 4:
Diện tích hình phẳng được giới hạn bởi parabol \(y=2-x^{2}\) và đường thẳng y=-x là
A. \(7\over2\)
B. \(9\over4\)
C. 3
D. \(9\over2\)
-
Câu 5:
Tìm a để diện tích S của hình phẳng giới hạn bởi \((P): y=\frac{x^{2}-2 x}{x-1}\), đường thẳng \(d: y=x-1 \text { và } x=a, x=2 a(a>1)\) bằng ln3.
A. a=1
B. a=4
C. a=3
D. a=2
-
Câu 6:
Tính diện tích S của hình phẳng giới hạn bởi các đường \(y=\mathrm{e}^{x}, y=2, x=0, x=1\)
A. \(S=4 \ln 2+\mathrm{e}-5\)
B. \(S=\mathrm{e}^{2}-7\)
C. \(S=4 \ln 2+\mathrm{e}-6\)
D. \(S=e-3\)
-
Câu 7:
Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số \(y=x;y=e^{x}\), trục tung và đường thẳng x =1 được tính theo công thức?
A. \(S=\int_{0}^{1}\left|\mathrm{e}^{x}-1\right| \mathrm{d} x\)
B. \(S=\int_{0}^{1}\left(e^{x}-x\right) d x\)
C. \(S=\int_{0}^{1}\left(x-e^{x}\right) d x\)
D. \(S=\int_{-1}^{1}\left|e^{x}-x\right| d x\)
-
Câu 8:
Diện tích hình phẳng giới hạn bởi các đường cong \(y=\sin x, y=\cos x\) và các đường thẳng x = 0 , x = π bằng ?
A. \(\sqrt2\)
B. \(2\sqrt2\)
C. \(-2\sqrt2\)
D. \(3\sqrt2\)
-
Câu 9:
Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số \(y=x^{2}+x-2, y=x+2\)và hai đường thẳng \(x=-2 ; x=3\). Diện tích của (H) bằng
A. \(\frac{87}{5}\)
B. \(\frac{87}{4}\)
C. \(\frac{87}{3}\)
D. \(\frac{87}{5}\)
-
Câu 10:
Tính diện tích hình phẳng tạo thành bởi parabol \(y=x^{2},y=-x+2\)và trục hoành trên đoạn [0;2] (phần gạch sọc trong hình vẽ)
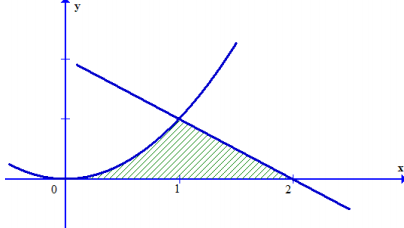
A. \(\frac{3}{5}\)
B. \(\frac{5}{6}\)
C. \(\frac{2}{3}\)
D. \(\frac{7}{6}\)
-
Câu 11:
Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục Ox hình phẳng giới hạn bởi các đường \(y=0, y=\sqrt{x}, y=x-2\)
A. \(\frac{8 \pi}{3}\)
B. \(\frac{16 \pi}{3}\)
C. \(10 \pi\)
D. \(8 \pi\)
-
Câu 12:
Cho hàm số f(x) liên tục trên [1;2]. Gọi (D) là hình phẳng giới hạn bởi các đồ thị hàm số \(y=f(x), y=0, x=1 \text { và } x=2\). Công thức tính diện tích S của (D) là công thức nào trong các công thức dưới đây?
A. \(S=\int_{1}^{2} f(x) \mathrm{d} x\)
B. \(S=\int_{1}^{2} f^{2}(x) \mathrm{d} x\)
C. \(S=\int_{1}^{2}|f(x)| \mathrm{d} x\)
D. \(S=\pi \int_{1}^{2} f^{2}(x) \mathrm{d} x\)
-
Câu 13:
Cho hình phẳng (H ) giới hạn bởi đồ thị của hai hàm số \(f_{1}(x) \text { và } f_{2}(x)\) liên tục trên đoạn \([a;b]\) và hai đường thẳng x =a, x =b (tham khảo hình vẽ dưới). Công thức tính diện tích của hình (H ) là:
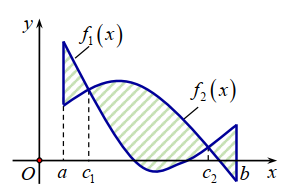
A. \(S=\int_{a}^{b}\left|f_{1}(x)-f_{2}(x)\right| \mathrm{d} x\)
B. \(S=\int_{a}^{b}\left(f_{1}(x)-f_{2}(x)\right) \mathrm{d} x\)
C. \(S=\int_{a}^{b}\left|f_{1}(x)+f_{2}(x)\right| \mathrm{d} x\)
D. \(S=\int_{a}^{b} f_{2}(x) \mathrm{d} x-\int_{a}^{b} f_{1}(x) \mathrm{d} x\)
-
Câu 14:
Cho hàm số\(y=x^{4}-3 x^{2}+m\) có đồ thị (Cm ) , với m là tham số thực. Giả sử (Cm ) cắt trục Ox tại bốn điểm phân biệt như hình vẽ
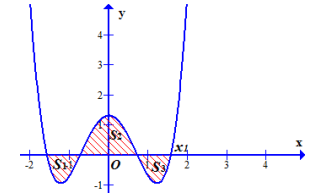
Gọi \(S_{1}, S_{2}, S_{3}\) là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để \(S_{1}+S_{3}=S_{2}\)
A. \(-\frac{5}{2}\)
B. \(\frac{5}{4}\)
C. \(-\frac{5}{4}\)
D. \(\frac{5}{2}\)
-
Câu 15:
Tính diện tích S của miền hình phẳng giới hạn bởi đồ thị của hàm số \(f(x)=a x^{3}+b x^{2}+c\) , các đường thẳng x =1, x = 2 và trục hoành (miền gạch chéo) cho trong hình dưới đây.
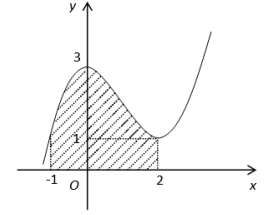
A. \(S=\frac{51}{8}\)
B. \(S=\frac{52}{8}\)
C. \(S=\frac{50}{8}\)
D. \(S=\frac{53}{8}\)
-
Câu 16:
Cho hình phẳng giới hạn bởi các đường\(y=x^{2}, y=0, x=0, x=4\) . Đường thẳng \(y=k(0<k<16)\) chia hình thành hai phần có diện tích \(S_{1}, S_{2}\) , (hình vẽ). Tìm k để \(S_{1}=S_{2}\)
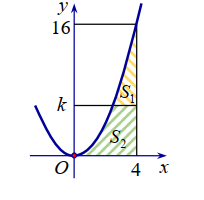
A. k=8
B. k=4
C. k=5
D. k=3
-
Câu 17:
Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}+2, x=1, x=2, y=0\)
A. \(S=\frac{10}{3}\)
B. \(S=\frac{8}{3}\)
C. \(S=\frac{13}{3}\)
D. \(S=\frac{5}{3}\)
-
Câu 18:
Tính diện tích miền hình phẳng giới hạn bởi các đường \(y=x^{2}-2 x, y=0, x=-10, x=10\)
A. \(S=\frac{2000}{3}\)
B. \(S=2008\)
C. \(S=\frac{2008}{3}\)
D. S=2000
-
Câu 19:
Cho hình phẳng như hình vẽ. Tính diện tích hình phẳng (H)
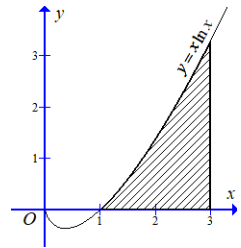
A. \(\frac{9}{2} \ln 3-2\)
B. \(1\)
C. \(\frac{9}{2} \ln 3-\frac{3}{2}\)
D. \(\frac{9}{2} \ln 3+2\)
-
Câu 20:
Cho hình thang cong (H ) giới hạn bởi các đường \(y=e^{x}, y=0, x=0, x=\ln 8\). Đường thẳng \(x=k(0<k<\ln 8)\) chia (H ) thành hai phần có diện tích là \(S_{1}\, và\, S_{2}\). Tìm k để \(S_{1}=S_{2}\)
A. \(k=\ln \frac{9}{2}\)
B. \(k=\ln 4\)
C. \(k=\frac{2}{3} \ln 4\)
D. \(k=\ln 5\)
-
Câu 21:
Tính diện tích hình phẳng giới hạn bởi các đường thẳng x = 4 , x = 9 và đường cong có phương trình \(y^{2}=8 x\)
A. \(\frac{76 \sqrt{2}}{3}\)
B. \(\frac{152}{3}\)
C. \(76 \sqrt{2}\)
D. \(\frac{152 \sqrt{2}}{3}\)
-
Câu 22:
Cho hình phẳng H giới hạn bởi các đường \(y=\sqrt{x} ; y=0 ; x=4\). Diện tích S của hình phẳng H bằng
A. \(16\over3\)
B. 3
C. \(15\over4\)
D. \(17\over3\)
-
Câu 23:
Hình phẳng giới hạn bởi các đường \(y=x^{2}-1, x=3 \text { và } O x\) có diện tích là
A. 8
B. \(\frac{4}{3}\)
C. \(\frac{16}{3}\)
D. \(\frac{20}{3}\)
-
Câu 24:
Diện tích của hình phẳng giới hạn bởi đồ thị hàm số \(y=x^{2}+x-2\) và trục hoành bằng
A. 9
B. \(\frac{13}{6}\)
C. \(\frac{9}{2}\)
D. \(\frac{3}{2}\)
-
Câu 25:
Diện tích của hình phẳng giới hạn bởi đồ thị hàm số \(y=\frac{1}{x} \ln x\), trục hoành và đường thẳng x = e bằng
A. \(1\over2\)
B. 1
C. \(1\over4\)
D. 2
-
Câu 26:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=x^3\), trục hoành và hai đường thẳng x = -1, x = 2 biết rằng mỗi đơn vị dài trên các trục tọa độ là 2 cm
A. 15
B. \(15\over4\)
C. \(17\over4\)
D. 17
-
Câu 27:
Diện tích hình phẳng giới hạn bởi đường cong \(y=x \ln x\), trục hoành và đường thẳng x=e là
A. \(\frac{e^{2}-1}{2}\)
B. \(\frac{e^{2}+1}{2}\)
C. \(\frac{e^{2}-1}{4}\)
D. \(\frac{e^{2}+1}{4}\)
-
Câu 28:
Diện tích hình phẳng giới hạn bởi đường cong \(y=x^{3}-4 x\) , trục hoành và hai đường thẳng \(x=-3, x=4\) là
A. \(\frac{202}{3}\)
B. \(\frac{203}{4}\)
C. \(\frac{201}{5}\)
D. \(\frac{201}{4}\)
-
Câu 29:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=-x^{2}+4\) , đường thẳng x = 3 , trục tung và trục hoành là
A. \(\frac{22}{3}\)
B. \(\frac{32}{3}\)
C. \(\frac{25}{3}\)
D. \(\frac{23}{3}\)
-
Câu 30:
Diện tích S hình phẳng giới hạn bởi các đường \(y=x^{3}+2 x+1\), trục hoành, x =1 và x = 2 là
A. \(S=\frac{31}{4}\)
B. \(S=\frac{49}{4}\)
C. \(S=\frac{21}{4}\)
D. \(S=\frac{39}{4}\)
-
Câu 31:
Cho parabol (P) có đồ thị như hình vẽ:
Tính diện tích hình phẳng giới hạn bởi (P) với trục hoành.
A. 4
B. 2
C. \(8\over3\)
D. \(4\over3\)
-
Câu 32:
Diện tích hình phẳng giới hạn bởi hàm số \(y=x^{2} \sqrt{x^{2}+1}\), trục Ox và đường thẳng x =1 bằng \(\frac{a \sqrt{b}-\ln (1+\sqrt{b})}{c}\) với a,b,c là các số nguyên dương. Khi đó giá trị của a+b+c là
A. 11
B. 12
C. 13
D. 14
-
Câu 33:
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \(y=x^{2}\) , trục hoành Ox , các đường thẳng x =1, x = 2 là
A. \(S=\frac{7}{3}\)
B. \(S=\frac{8}{3}\)
C. \(S=7\)
D. \(S=8\)
-
Câu 34:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \(y=e^{x}+e^{-x}\), trục hoành, trục tung và đường thẳng x = -2
A. \(S=\frac{\mathrm{e}^{4}+1}{\mathrm{e}^{2}}(\text { đvdt })\)
B. \(S=\frac{\mathrm{e}^{4}-1}{\mathrm{e}}(\text { đvdt })\)
C. \(S=\frac{\mathrm{e}^{2}-1}{\mathrm{e}}(\text { đvdt })\)
D. \(S=\frac{\mathrm{e}^{4}-1}{\mathrm{e}^{2}}(\text { đvdt })\)
-
Câu 35:
Tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiabg2 % da9maapehabaWaaSaaaeaacaWG4bWaaWbaaSqabeaacaaIYaGaaGim % aiaaigdacaaI4aaaaaGcbaGaaeyzamaaCaaaleqabaGaamiEaaaaki % abgUcaRiaaigdaaaGaaeizaiaadIhaaSqaaiabgkHiTiaaikdaaeaa % caaIYaaaniabgUIiYdaaaa!466A! I = \int\limits_{ - 2}^2 {\frac{{{x^{2018}}}}{{{{\rm{e}}^x} + 1}}{\rm{d}}x} \)
A. 0
B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiabg2 % da9maalaaabaGaaGOmamaaCaaaleqabaGaaGOmaiaaicdacaaIYaGa % aGimaaaaaOqaaiaaikdacaaIWaGaaGymaiaaiMdaaaaaaa!3EAB! I = \frac{{{2^{2020}}}}{{2019}}\)
C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiabg2 % da9maalaaabaGaaGOmamaaCaaaleqabaGaaGOmaiaaicdacaaIXaGa % aGyoaaaaaOqaaiaaikdacaaIWaGaaGymaiaaiMdaaaaaaa!3EB3! I = \frac{{{2^{2019}}}}{{2019}}\)
D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiabg2 % da9maalaaabaGaaGOmamaaCaaaleqabaGaaGOmaiaaicdacaaIXaGa % aGyoaaaaaOqaaiaaikdacaaIWaGaaGymaiaaiMdaaaaaaa!3EB3! I = \frac{{{2^{2018}}}}{{2018}}\)
-
Câu 36:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y=\cos 2 x\) , trục hoành và hai đường thẳng \(x=0, x=\frac{\pi}{2}\) là:
A. 2
B. 1
C. 3
D. 4
-
Câu 37:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số\(y=\cos x\) , trục tung, trục hoành và đường thẳng \(x =\pi\) bằng
A. 3
B. 2
C. 4
D. 1
-
Câu 38:
Cho f(x); g(x) là hai hàm liên tục trên đoạn [-1;1]. f(x) là hàm chẵn, g(x) là hàm lẽ . Biết \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaca % WGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaaeizaiaadIhacqGH % 9aqpcaaI1aaaleaacaaIWaaabaGaaGymaaqdcqGHRiI8aaaa!40EB! \int\limits_0^1 {f\left( x \right){\rm{d}}x = 5} \)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaca % WGNbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaaeizaiaadIhacqGH % 9aqpcaaI3aGaaGPaVdWcbaGaaGimaaqaaiaaigdaa0Gaey4kIipaaa % a!4279! ; \int\limits_0^1 {g\left( x \right){\rm{d}}x = 7\,} \). Mệnh đề nào sau đây sai ?
A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaca % WGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaaeizaiaadIhacqGH % 9aqpcaaIXaGaaGimaaWcbaGaeyOeI0IaaGymaaqaaiaaigdaa0Gaey % 4kIipaaaa!428F! \int\limits_{ - 1}^1 {f\left( x \right){\rm{d}}x = 10} \)
B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaada % WadaqaaiaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGHRaWk % caWGNbWaaeWaaeaacaWG4baacaGLOaGaayzkaaaacaGLBbGaayzxaa % GaaeizaiaadIhacqGH9aqpcaaIXaGaaGimaaWcbaGaeyOeI0IaaGym % aaqaaiaaigdaa0Gaey4kIipaaaa!48D5! \int\limits_{ - 1}^1 {\left[ {f\left( x \right) + g\left( x \right)} \right]{\rm{d}}x = 10} \)
C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaada % WadaqaaiaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGHsisl % caWGNbWaaeWaaeaacaWG4baacaGLOaGaayzkaaaacaGLBbGaayzxaa % GaaeizaiaadIhacqGH9aqpcaaIXaGaaGimaaWcbaGaeyOeI0IaaGym % aaqaaiaaigdaa0Gaey4kIipaaaa!48E0! \int\limits_{ - 1}^1 {\left[ {f\left( x \right) - g\left( x \right)} \right]{\rm{d}}x = 10} \)
D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaca % WGNbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaaeizaiaadIhacqGH % 9aqpcaaIXaGaaGinaaWcbaGaeyOeI0IaaGymaaqaaiaaigdaa0Gaey % 4kIipaaaa!4294! \int\limits_{ - 1}^1 {g\left( x \right){\rm{d}}x = 14} \)
-
Câu 39:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y=\frac{x+1}{x+2}\), trục hoành và đường thẳng x = 2 là
A. \(3+2 \ln 2\)
B. \(3-\ln 2\)
C. \(3-2 \ln 2\)
D. \(3+\ln 2\)
-
Câu 40:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y=x^{4}-3 x^{2}-4\) trục hoành và hai đường thẳng x = 0, x = 3 là
A. \(\frac{142}{5}\)
B. \(\frac{143}{5}\)
C. \(\frac{144}{5}\)
D. \(\frac{141}{5}\)
-
Câu 41:
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y=x^{3}-3 x^{2}\) , trục hoành và hai đường thẳng x = 1, x = 4 là
A. \(\frac{53}{4}\)
B. \(\frac{51}{4}\)
C. \(\frac{49}{4}\)
D. \(\frac{25}{2}\)
-
Câu 42:
Tìm khẳng định đúng trong các khẳng định sau
A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaci % GGZbGaaiyAaiaac6gadaqadaqaaiaaigdacqGHsislcaWG4baacaGL % OaGaayzkaaGaaeizaiaadIhaaSqaaiaaicdaaeaacaaIXaaaniabgU % IiYdGccqGH9aqpdaWdXbqaaiGacohacaGGPbGaaiOBaiaadIhacaqG % KbGaamiEaaWcbaGaaGimaaqaaiaaigdaa0Gaey4kIipaaaa!4D63! \int\limits_0^1 {\sin \left( {1 - x} \right){\rm{d}}x} = \int\limits_0^1 {\sin x{\rm{d}}x} \)
B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaci % GGJbGaai4BaiaacohadaqadaqaaiaaigdacqGHsislcaWG4baacaGL % OaGaayzkaaGaaeizaiaadIhaaSqaaiaaicdaaeaacaaIXaaaniabgU % IiYdGccqGH9aqpcqGHsisldaWdXbqaaiGacogacaGGVbGaai4Caiaa % dIhacaqGKbGaamiEaaWcbaGaaGimaaqaaiaaigdaa0Gaey4kIipaaa % a!4E46! \int\limits_0^1 {\cos \left( {1 - x} \right){\rm{d}}x} = - \int\limits_0^1 {\cos x{\rm{d}}x} \)
C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaci % GGJbGaai4BaiaacohadaWcaaqaaiaadIhaaeaacaaIYaaaaiaabsga % caWG4baaleaacaaIWaaabaGaeqiWdahaniabgUIiYdGccqGH9aqpda % WdXbqaaiGacogacaGGVbGaai4CaiaadIhacaqGKbGaamiEaaWcbaGa % aGimaaqaamaalaaabaGaeqiWdahabaGaaGOmaaaaa0Gaey4kIipaaa % a!4DC4! \int\limits_0^\pi {\cos \frac{x}{2}{\rm{d}}x} = \int\limits_0^{\frac{\pi }{2}} {\cos x{\rm{d}}x} \)
D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaci % GGZbGaaiyAaiaac6gadaWcaaqaaiaadIhaaeaacaaIYaaaaiaabsga % caWG4baaleaacaaIWaaabaGaeqiWdahaniabgUIiYdGccqGH9aqpda % WdXbqaaiGacohacaGGPbGaaiOBaiaadIhacaqGKbGaamiEaaWcbaGa % aGimaaqaamaalaaabaGaeqiWdahabaGaaGOmaaaaa0Gaey4kIipaaa % a!4DCE! \int\limits_0^\pi {\sin \frac{x}{2}{\rm{d}}x} = \int\limits_0^{\frac{\pi }{2}} {\sin x{\rm{d}}x} \)
-
Câu 43:
Gọi S là diện tích miền hình phẳng được tô đậm trong hình vẽ bên. Công thức tính S là
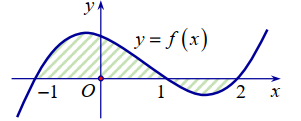
A. \(S=\int_{-1}^{1} f(x) \mathrm{d} x+\int_{1}^{2} f(x) \mathrm{d} x\)
B. \(S=\int_{-1}^{1} f(x) \mathrm{d} x-\int_{1}^{2} f(x) \mathrm{d} x\)
C. \(S=\int_{-1}^{2} f(x) \mathrm{d} x\)
D. \(S=-\int_{-1}^{2} f(x) \mathrm{d} x\)
-
Câu 44:
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị (C) là đường cong như hình bên. Diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và hai đường thẳng x = 0 , x = 2 (phần tô đen) là
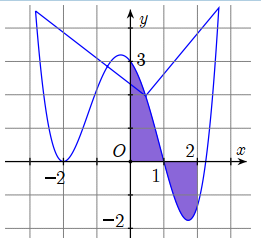
A. \(\int_{0}^{2} f(x) \mathrm{d} x\)
B. \(-\int_{0}^{1} f(x) \mathrm{d} x+\int_{1}^{2} f(x) \mathrm{d} x\)
C. \(\int_{0}^{1} f(x) \mathrm{d} x-\int_{1}^{2} f(x) \mathrm{d} x\)
D. \(\left|\int_{0}^{2} f(x) \mathrm{d} x\right|\)
-
Câu 45:
Biết \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaada % WcaaqaaiGacYgacaGGUbGaamiEaaqaamaakaaabaGaamiEaaWcbeaa % aaGccaqGKbGaamiEaaWcbaGaaGymaaqaaiaadwgaa0Gaey4kIipaki % abg2da9iaadggadaGcaaqaaiaadwgaaSqabaGccqGHRaWkcaWGIbaa % aa!44C6! \int\limits_1^e {\frac{{\ln x}}{{\sqrt x }}{\rm{d}}x} = a\sqrt e + b\) với a, b thuộc Z . Tính P = ab
A. 4
B. -8
C. -4
D. 8
-
Câu 46:
Diện tích của hình phẳng (H) được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng\(x=a, x=b(a<b)\) (phần tô đậm trong hình vẽ) tính theo công thức:
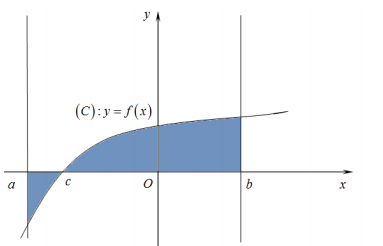
A. \(S=\int_{a}^{b} f(x) \mathrm{d} x\)
B. \(S=-\int_{a}^{c} f(x) \mathrm{d} x+\int_{c}^{b} f(x) \mathrm{d} x\)
C. \(S=\left|\int_{a}^{b} f(x) \mathrm{d} x\right|\)
D. \(S=\int_{a}^{c} f(x) \mathrm{d} x+\int_{c}^{b} f(x) \mathrm{d} x\)
-
Câu 47:
Xét hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn điều kiện f(1) = 1 ; f(2) = 44. Tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOsaiabg2 % da9maapehabaWaaeWaaeaadaWcaaqaaiqadAgagaqbamaabmaabaGa % amiEaaGaayjkaiaawMcaaiabgUcaRiaaikdaaeaacaWG4baaaiabgk % HiTmaalaaabaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiab % gUcaRiaaigdaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaaaaaOGaay % jkaiaawMcaaiaabsgacaWG4baaleaacaaIXaaabaGaaGOmaaqdcqGH % RiI8aaaa!4D39! J = \int\limits_1^2 {\left( {\frac{{f'\left( x \right) + 2}}{x} - \frac{{f\left( x \right) + 1}}{{{x^2}}}} \right){\rm{d}}x} \)
A. J = 1 + ln4
B. J = 4 - ln2
C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOsaiabg2 % da9iGacYgacaGGUbGaaGOmaiabgkHiTmaalaaabaGaaGymaaqaaiaa % ikdaaaaaaa!3CDD! J = \ln 2 - \frac{1}{2}\)
D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOsaiabg2 % da9maalaaabaGaaGymaaqaaiaaikdaaaGaey4kaSIaciiBaiaac6ga % caaI0aaaaa!3CD4! J = \frac{1}{2} + \ln 4\)
-
Câu 48:
Cho hàm số f(x) liên tục trên \(\mathbb{R}\) , có đồ thị như hình vẽ. Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hàm số f(x ) , trục hoành và trục tung. Khẳng định nào sau đây đúng?
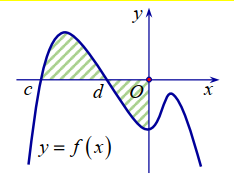
A. \(S=\int_{c}^{d} f(x) \mathrm{d} x-\int_{d}^{0} f(x) \mathrm{d} x\)
B. \(S=-\int_{c}^{d} f(x) \mathrm{d} x-\int_{d}^{0} f(x) \mathrm{d} x\)
C. \(S=-\int_{c}^{d} f(x) \mathrm{d} x+\int_{d}^{0} f(x) \mathrm{d} x\)
D. \(S=\int_{c}^{d} f(x) \mathrm{d} x+\int_{d}^{0} f(x) \mathrm{d} x\)
-
Câu 49:
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Hình phẳng được đánh dấu trong hình vẽ bên có diện tích là:
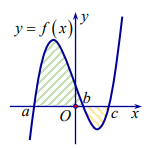
A. \(\int_{a}^{b} f(x) \mathrm{d} x-\int_{b}^{c} f(x) \mathrm{d} x\)
B. \(\int_{a}^{b} f(x) \mathrm{d} x+\int_{b}^{c} f(x) \mathrm{d} x\)
C. \(-\int_{a}^{b} f(x) \mathrm{d} x+\int_{b}^{c} f(x) \mathrm{d} x\)
D. \(\int_{a}^{b} f(x) \mathrm{d} x-\int_{c}^{b} f(x) \mathrm{d} x\)
-
Câu 50:
Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y=f(x), trục Ox và các đường thẳng \(x=a, x=b(a<b)\)
A. \( \int_{a}^{b}|f(x)| d x\)
B. \(\int_{a}^{b} f^{2}(x) d x\)
C. \(\int_{a}^{b} f(x) d x\)
D. \(\pi \int_{a}^{b} f(x) d x\)
