Trắc nghiệm Tích phân Toán Lớp 12
-
Câu 1:
Tích phân \(I=\int_{1}^{2} 2 x \cdot d x\) có giá trị là
A. I=1
B. I=2
C. I=3
D. I=4
-
Câu 2:
Giá trị nào của b để \(\int_{1}^{b}(2 x-6) d x=0 ?\)
A. \(\left[ \begin{array}{l} b = 0\\ b = 1 \end{array} \right.\)
B. \(\left[ \begin{array}{l} b = 0\\ b = 1 \end{array} \right.\)
C. \(\left[ \begin{array}{l} b = 5\\ b = 0 \end{array} \right.\)
D. \(\left[ \begin{array}{l} b = 1\\ b = 5 \end{array} \right.\)
-
Câu 3:
Cho \(\int_{0}^{3} f(x) \mathrm{d} x=a, \int_{2}^{3} f(x) \mathrm{d} x=b . \text { Khi đó } \int_{0}^{2} f(x) \mathrm{d} x\) bằng?
A. -a-b
B. b-a
C. a+b
D. a-b
-
Câu 4:
\(\text { Đặt } I=\int_{1}^{2}(2 m x+1) \mathrm{d} x\) ( là tham số thực). Tìm để I=4
A. m=-1
B. m=-2
C. m=1
D. m=2
-
Câu 5:
Biết \(\int_{a}^{b}(2 x-1) d x=1\) . Khẳng định nào sau đây là đúng?
A. \(b-a=1\)
B. \(a^{2}-b^{2}=a-b-1\)
C. \(b^{2}-a^{2}=b-a+1\)
D. \(a-b=1\)
-
Câu 6:
Cho hàm số \(y=f(x)=\left\{\begin{array}{lll} 6 x^{2} & \text { khi } & x \leq 0 \\ a-a^{2} x & \text { khi } & x \geq 0 \end{array} \text { và } I=\int_{-1}^{4} f(x) \mathrm{d} x\right.\). Hỏi có tất cả bao nhiêu số nguyên \(I+22 \geq 0 ?\)
A. 2
B. 3
C. 4
D. 5
-
Câu 7:
Cho hàm số \(y=f(x)=\left\{\begin{array}{lll} \frac{2}{x+1} & \text { khi } & 0 \leq x \leq 1 \\ 2 x-1 & \text { khi } & 1 \leq x \leq 3 \end{array}\right.\). Tính \(\int_{0}^{3} f(x) \mathrm{d} x\)
A. \(6+\ln 4\)
B. \(4+\ln 4\)
C. \(6+\ln 2\)
D. \(2+2 \ln 2\)
-
Câu 8:
Cho hàm số \(y=f(x)=\left\{\begin{array}{ll} 3 x^{2} & \text { khi } 0 \leq x \leq 1 \\ 4-x & \text { khi } 1 \leq x \leq 2 \end{array}\right.\) . Tính tích phân \(\int_{0}^{2} f(x) \mathrm{d} x\)
A. \(7\over2\)
B. 1
C. \(5\over2\)
D. \(3\over2\)
-
Câu 9:
Tính tích phân \(I=\int_{0}^{1} x^{2018}(1+x) \mathrm{d} x\).
A. \(I=\frac{1}{2018}+\frac{1}{2019}\)
B. \(I=\frac{1}{2020}+\frac{1}{2021}\)
C. \(I=\frac{1}{2019}+\frac{1}{2020}\)
D. \(I=\frac{1}{2017}+\frac{1}{2018}\)
-
Câu 10:
Tính \(I=\int_{0}^{1}\left(\frac{1}{2 x+1}+3 \sqrt{x}\right) \mathrm{d} x\)
A. \(2+\ln \sqrt{3}\)
B. \(4+\ln 3\)
C. \(2+\ln 3\)
D. \(1+\ln \sqrt{3}\)
-
Câu 11:
Tính tích phân \(I=\int_{1}^{20018} \frac{\mathrm{d} x}{x}\)
A. \(I=2018 . \ln 2-1\)
B. \(I=2^{2018}\)
C. \(I=2018 . \ln 2\)
D. \(I=2018\)
-
Câu 12:
Tính tích phân \(I=\int_{0}^{3} \frac{\mathrm{d} x}{x+2}\)
A. \(I=\frac{4581}{5000}\)
B. \(I=\log \frac{5}{2}\)
C. \(I=\ln \frac{5}{2}\)
D. \(I=-\frac{21}{100}\)
-
Câu 13:
Cho hàm số \(f(x)=\frac{a}{x^{2}}+\frac{b}{x}+2, \text { với } a, b\) là các số hữu tỉ thỏa điều kiện \(\int_{\frac{1}{2}}^{1} f(x) \mathrm{d} x=2-3 \ln 2\).Tính T= a+b.
A. T=-1
B. T=2
C. T=-2
D. T=0
-
Câu 14:
Cho hàm số f(x)20 có đạo hàm liên tục trên đoạn [-1;3] và thỏa mãn \(f(-1)=4 ; f(3)=7\) Giá trị của \(I=\int_{-1}^{3} 5 f^{\prime}(x) \mathrm{d} x\) là:
A. 20
B. 3
C. 10
D. 15
-
Câu 15:
Cho hàm số y=f(x) thoả mãn điều kiện f (1) =12 , f'(x) liên tục trên \(\mathbb{R} \text { và } \int_{1}^{4} f^{\prime}(x) \mathrm{d} x=17\) Khi đó f (4) bằng
A. 5
B. 29
C. 19
D. 9
-
Câu 16:
Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các đường y = f(x), trục Ox và hai đường thẳng x = a, x = b xung quanh trục Ox.
A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiWda3aa8 % qCaeaacaWGMbWaaWbaaSqabeaacaaIYaaaaOWaaeWaaeaacaWG4baa % caGLOaGaayzkaaGaaGPaVlaabsgacaWG4baaleaacaWGHbaabaGaam % OyaaqdcqGHRiI8aOGaaGPaVdaa!454E! \pi \int\limits_a^b {{f^2}\left( x \right)\,{\rm{d}}x} \,\)
B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaca % WGMbWaaWbaaSqabeaacaaIYaaaaOWaaeWaaeaacaWG4baacaGLOaGa % ayzkaaGaaGPaVlaabsgacaWG4baaleaacaWGHbaabaGaamOyaaqdcq % GHRiI8aOGaaGPaVdaa!4391! \int\limits_a^b {{f^2}\left( x \right)\,{\rm{d}}x} \,\)
C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiWda3aa8 % qCaeaacaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaaGPaVlaa % bsgacaWG4baaleaacaWGHbaabaGaamOyaaqdcqGHRiI8aOGaaGPaVd % aa!445B! \pi \int\limits_a^b {f\left( x \right)\,{\rm{d}}x} \,\)
D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmaiabec % 8aWnaapehabaGaamOzamaaCaaaleqabaGaaGOmaaaakmaabmaabaGa % amiEaaGaayjkaiaawMcaaiaaykW7caqGKbGaamiEaaWcbaGaamyyaa % qaaiaadkgaa0Gaey4kIipakiaaykW7aaa!460A! 2\pi \int\limits_a^b {{f^2}\left( x \right)\,{\rm{d}}x} \,\)
-
Câu 17:
Cho hàm số f (x) liên tục trên \([0 ; 1] \text { và } f(1)-f(0)=2\). Tính \(\int_{0}^{1} f^{\prime}(x) \mathrm{d} x\)
A. I=-1
B. I=1
C. I=2
D. I=0
-
Câu 18:
Cho hàm số f(x) có đạo hàm liên tục trên đoạn \([a ; b] \text { và } f(a)=-2, f(b)=-4\).. Tính \(T=\int_{a}^{b} f^{\prime}(x) \mathrm{d} x\)
A. -6
B. 2
C. 6
D. -2
-
Câu 19:
Cho \(\int_{a}^{b} f^{\prime}(x) \mathrm{d} x=7 \text { và } f(b)=5\) . Khi đó \(f(a)\) 12bằng
A. 12
B. 0
C. 2
D. -2
-
Câu 20:
Cho hàm f(x) có đạo hàm liên tục trên [a;b] đồng thời \(f(2)=2, f(3)=5\) . Tính \(\int_{2}^{3} f^{\prime}(x) \mathrm{d} x\)
A. -3
B. 7
C. 10
D. 3
-
Câu 21:
Cho \(\int_{-2}^{1} f(x) \mathrm{d} x=3\) . Tính tích phân \(I=\int_{-2}^{1}[2 f(x)-1] \mathrm{d} x\)
A. -9
B. -3
C. 3
D. 5
-
Câu 22:
Tích phân \(\int_{a}^{b} f(x) d x\) được phân tích thành
A. \(\begin{aligned} &\int_{c}^{b} f(x)dx-\int_{c}^{a}f(x) d x \end{aligned}\)
B. \( \int_{c}^{b} f(x)dx-\int_{c}^{a}-f(x) d x\)
C. \(\int_{c}^{b} f(x)dx+\int_{c}^{a} f(x) d x\)
D. \(-\int_{c}^{b} f(x)dx+\int_{c}^{a} f(x) d x\)
-
Câu 23:
Cho tích phân \(I_{1}=\int_{a}^{b} f(x) d x=m \text { và } I_{2}=\int_{c}^{a} f(x) d x=n\) . Tích phân \(I=\int_{c}^{b} f(x) d x\) có giá trị là
A. m+n
B. m-n
C. -m-n
D. Không thể xác định.
-
Câu 24:
Cho hai tích phân \(\int_{-\pi}^{a} f(x) d x=m \text { và } \int_{-\pi}^{a} g(x) d x=n\) . Giá trị của tích phân \(\int_{-a}^{a}[f(x)-g(x)] d x\) là:
A. m-n
B. n-m
C. m+n
D. Không thể xác định.
-
Câu 25:
Cho hàm số y=f(x) liên tục trên [a;b], có đồ thị y=f'(x) như hình vẽ sau
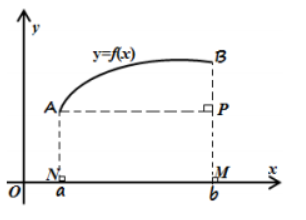
Mệnh đề nào dưới đây đúng?
A. \(\int_{a}^{b} f^{\prime}(x) \mathrm{d} x\) là diện tích hình thang ABMN.
B. \(\int_{a}^{b} f^{\prime}(x) \mathrm{d} x\) là độ dài đoạn BP
C. \(\int_{a}^{b} f^{\prime}(x) \mathrm{d} x\) là độ dài đoạn MN.
D. \(\int_{a}^{b} f^{\prime}(x) \mathrm{d} x\) là độ dài đoạn cong AB.
-
Câu 26:
Cho F(x) là một nguyên hàm của hàm số f(x) . Khi đó hiệu số \(F(0)-F(1)\) bằng
A. \(\int_{0}^{1} f(x) \mathrm{d} x\)
B. \(\int_{0}^{1}-F(x) \mathrm{d} x\)
C. \(\int_{0}^{1}-F(x) \mathrm{d} x .\)
D. \(\int_{0}^{1}-f(x) \mathrm{d} x\)
-
Câu 27:
Cho hàm số f(x) liên tục trên đoạn [a;b] . Mệnh đề nào dưới đây sai?
A. \(\int_{a}^{b} f(x) \mathrm{d} x=-\int_{b}^{a} f(x) \mathrm{d} x\)
B. \(\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{c} f(x) \mathrm{d} x+\int_{c}^{b} f(x) \mathrm{d} x\,,\forall c\in\mathbb{R}\)
C. \(\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{b} f(t) \mathrm{d} t\)
D. \(\int_{a}^{a} f(x) \mathrm{d} x=0\)
-
Câu 28:
Giả sử là hàm số f(x) liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng K. Khẳng định nào sau đây sai?
A. \(\int_{a}^{a} f(x) d x=1\)
B. \(\int_{a}^{b} f(x) d x=-\int_{b}^{a} f(x) d x\)
C. \(\int_{a}^{c} f(x) d x+\int_{c}^{b} f(x) d x=\int_{a}^{b} f(x) d x, c \in(a ; b)\)
D. \(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(t) d t\)
-
Câu 29:
Cho hàm số \(y=f(x)\) liên tục trên đoạn [a;b] . Mệnh đề nào dưới đây sai?
A. \(\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{b} f(t) \mathrm{d} t\)
B. \(\int_{a}^{b} f(x) \mathrm{d} x=-\int_{b}^{a} f(x) \mathrm{d} x\)
C. \(\int_{a}^{b} k \mathrm{d} x=k(a-b), \forall k \in \mathbb{R}\)
D. \(\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{c} f(x) \mathrm{d} x+\int_{c}^{b} f(x) \mathrm{d} x, \forall c \in(a ; b)\)
-
Câu 30:
Cho hàm số f(t) liên tục trên \(K\text{ và }a, b \in K, F(t)\) là một nguyên hàm của trên K . Chọn khẳng định sai trong các khẳng định sau
A. \(F(a)-F(b)=\int_{a}^{b} f(t) \mathrm{d} t\)
B. \(\int_{a}^{b} f(t) \mathrm{d} t=\left.F(t)\right|_{a} ^{b}\)
C. \(\int_{a}^{b} f(t) \mathrm{d} t=\left.\left(\int f(t) \mathrm{d} t\right)\right|_{a} ^{b}\)
D. \(\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{b} f(t) \mathrm{d} t\)
-
Câu 31:
Cho hàm số y=f(x) liên tục trên khoảng\(K\,\, và\,\, a, b, c \in K\) Mệnh đề nào sau đây sai?
A. \(\int_{a}^{b} f(x) \mathrm{d} x+\int_{c}^{b} f(x) \mathrm{d} x=\int_{a}^{c} f(x) \mathrm{d} x\)
B. \(\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{b} f(t) \mathrm{d} \mathrm{t}\)
C. \(\int_{a}^{b} f(x) \mathrm{d} x=-\int_{b}^{a} f(x) \mathrm{d} x\)
D. \(\int_{a}^{a} f(x) \mathrm{d} x=0\)
-
Câu 32:
Cho f(x) là hàm số liên tục trên đoạn \([a ; b] \text { và } c \in[a ; b]\) . Tìm mệnh đề đúng trong các mệnh đề sau.
A. \(\int_{a}^{c} f(x) \mathrm{d} x+\int_{c}^{b} f(x) \mathrm{d} x=\int_{b}^{a} f(x) \mathrm{d} x\)
B. \(\int_{a}^{b} f(x) \mathrm{d} x+\int_{a}^{c} f(x) \mathrm{d} x=\int_{c}^{b} f(x) \mathrm{d} x\)
C. \(\int_{a}^{b} f(x) \mathrm{d} x-\int_{a}^{c} f(x) \mathrm{d} x=\int_{c}^{c} f(x) \mathrm{d} x\)
D. \(\int_{a}^{b} f(x) \mathrm{d} x+\int_{c}^{a} f(x) \mathrm{d} x=\int_{c}^{b} f(x) \mathrm{d} x\)
-
Câu 33:
Cho hai số thực , tùy ý, là một nguyên hàm của hàm số trên tập \(\mathbb{R}\) . Mệnhđề nào dưới đây là đúng?
A. \(\begin{aligned} &\int_{a}^{b} f(x) \mathrm{d} x=f(b)-f(a) . \end{aligned}\)
B. \(\int_{a}^{b} f(x) \mathrm{d} x=F(b)-F(a)\)
C. \(\int_{a}^{b} f(x) \mathrm{d} x=F(a)-F(b)\)
D. \( \int_{a}^{b} f(x) \mathrm{d} x=F(b)+F(a)\)
-
Câu 34:
Cho hai hàm số \(f(x)\) và \(g(x)\) liên tục trên \(K, a, b \in K\). Khẳng định nào sau đây là khẳng định sai?
A. \(\int_{a}^{b}[f(x)+g(x)] \mathrm{d} x=\int_{a}^{b} f(x) \mathrm{d} x+\int_{a}^{b} g(x) \mathrm{d} x\)
B. \(\int_{a}^{b} k f(x) \mathrm{d} x=k \int_{a}^{b} f(x) \mathrm{d} x\)
C. \(\int_{a}^{b} f(x) g(x) \mathrm{d} x=\int_{a}^{b} f(x) \mathrm{d} x \cdot \int_{a}^{b} g(x) \mathrm{d} x\)
D. \(\int_{a}^{b}[f(x)-g(x)] \mathrm{d} x=\int_{a}^{b} f(x) \mathrm{d} x-\int_{a}^{b} g(x) \mathrm{d} x\)
-
Câu 35:
Khẳng định nào sau đây sai?
A. \(\begin{aligned} &\int_{a}^{b}[f(x)+g(x)] \mathrm{d} x=\int_{a}^{b} f(x) \mathrm{d} x+\int_{a}^{b} g(x) \mathrm{d} x \end{aligned}\)
B. \(\int_{a}^{b} f(x) \mathrm{d} x=\int_{c}^{b} f(x) \mathrm{d} x+\int_{a}^{c} f(x) \mathrm{d} x\)
C. \(\int_{a}^{b} f(x) \mathrm{d} x=\int_{b}^{a} f(x) \mathrm{d} x\)
D. \(\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{b} f(t) \mathrm{d} t\)
-
Câu 36:
Cho hàm số \(y=f(x), y=g(x)\) , liên tục trên [a;b] và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai?
A. \(\begin{array}{l} \int_{a}^{b} f(x) \mathrm{d} x=-\int_{b}^{a} f(x) \mathrm{d} x \end{array}\)
B. \(\int_{a}^{b} x f(x) \mathrm{d} x=x \int_{a}^{b} f(x) \mathrm{d} x \)
C. \(\int_{a}^{a} k f(x) \mathrm{d} x=0 \)
D. \(\int_{a}^{b}[f(x)+g(x)] \mathrm{d} x=\int_{a}^{b} f(x) \mathrm{d} x+\int_{a}^{b} g(x) \mathrm{d} x\)
-
Câu 37:
Cho (H ) là hình phẳng giới hạn bởi các đồ thị hàm số \(y=\mathrm{e}, y=\mathrm{e}^{x} \text { và } y=(1-\mathrm{e}) x+1\) (tham khảo hình vẽ bên).
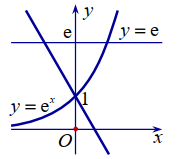
Diện tích hình phẳng (H ) là
A. \(S=\frac{\mathrm{e}+1}{2}\)
B. \(S=e+\frac{3}{2}\)
C. \(S=\frac{\mathrm{e}-1}{2}\)
D. \(S=\mathrm{e}+\frac{1}{2}\)
-
Câu 38:
Tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số \(y=2 x^{2} \text { và } y=5 x-2\)
A. \(S=\frac{5}{4}\)
B. \(S=\frac{5}{8}\)
C. \(S=\frac{9}{8}\)
D. \(S=\frac{9}{4}\)
-
Câu 39:
Cho hình phẳng (H ) giới hạn bởi các đường \(y=\left|x^{2}-4 x+3\right|, y=x+3\) (phần tô đậm trong hình vẽ). Diện tích của (H ) bằng
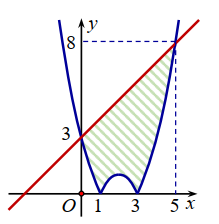
A. \(\frac{37}{2}\)
B. \(\frac{109}{6}\)
C. \(\frac{454}{25}\)
D. \(\frac{91}{5}\)
-
Câu 40:
Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2};y=x+2\) là:
A. S=9
B. \(S=\frac{9}{4}\)
C. \(S=\frac{9}{2}\)
D. \(S=\frac{8}{9}\)
-
Câu 41:
Tính diện tích S của hình phẳng (H ) giới hạn bởi đường cong \(y=-x^{3}+12 x \text { và } y=-x^{2}\)
A. \(S=\frac{343}{12}\)
B. \(S=\frac{793}{4}\)
C. \(S=\frac{397}{4}\)
D. \(S=\frac{937}{12}\)
-
Câu 42:
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số (H): \(y=\frac{x-1}{x+1}\) và các trục tọa độ. Khi đó giá trị của S bằng
A. \(S=\ln 2-1(\text { đvdt })\)
B. \(S=2 \ln 2-1(\text { đvdt })\)
C. \(S=2 \ln 2+1(\text { đvdt })\)
D. \(S=\ln 2+1(\text { đvdt })\)
-
Câu 43:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số \(y=x^{3}-x, y=x-x^2\)
A. S=13
B. \(S=\frac{81}{12}\)
C. \(S=\frac{9}{4}\)
D. \(S=\frac{37}{12}\)
-
Câu 44:
Cho (H ) là hình phẳng giới hạn bởi các đường\(y=\sqrt{2 x} ; y=2 x-2\) và trục hoành. Tính diện tích của (H ) .
A. \(\frac{5}{3}\)
B. \(\frac{16}{3}\)
C. \(\frac{10}{3}\)
D. \(\frac{8}{3}\)
-
Câu 45:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=-x^{3}+3 x+3\) và đường thẳng y=5 là:
A. \(\frac{5}{4}\)
B. \(\frac{45}{4}\)
C. \(\frac{27}{4}\)
D. \(\frac{21}{4}\)
-
Câu 46:
Cho (H ) là hình phẳng giới hạn bởi parabol \(y=\sqrt{3} x^{2}\), cung tròn có phương trình \(y=\sqrt{4-x^{2}} \quad(\text { vói } 0 \leq x \leq 2)\) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H ) bằng
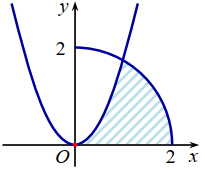
A. \(\frac{4 \pi+\sqrt{3}}{12}\)
B. \(\frac{4 \pi-\sqrt{3}}{6}\)
C. \(\frac{4 \pi+2 \sqrt{3}-3}{6}\)
D. \(\frac{5 \sqrt{3}-2 \pi}{3}\)
-
Câu 47:
Tính diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}, y=-\frac{1}{3} x+\frac{4}{3}\) và trục hoành.
A. \(\frac{11}{6}\)
B. \(\frac{61}{3}\)
C. \(\frac{343}{162}\)
D. \(\frac{39}{2}\)
-
Câu 48:
Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số \(y=\left|x^{2}-4 x+3\right|, y=x+3\). Diện tích của (H) bằng
A. \(\frac{108}{5}\)
B. \(\frac{109}{5}\)
C. \(\frac{109}{6}\)
D. \(\frac{119}{6}\)
-
Câu 49:
Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số\(y=\left|x^{2}-1\right|, y=|x|+5\) . Diện tích của (H) bằng
A. \(\frac{71}{3}\)
B. \(\frac{73}{3}\)
C. \(\frac{70}{3}\)
D. \(\frac{74}{3}\)
-
Câu 50:
Gọi (H) là hình phẳng được giới hạn bởi đồ thị hai hàm số \(y=\left(1+e^{x}\right) x, y=(1+e) x\) Diện tích của (H) bằng
A. \(\frac{e-1}{2}\)
B. \(\frac{e-2}{2}\)
C. \(\frac{e-2}{2}\)
D. \(\frac{e+1}{2}\)














