Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán Lớp 12
-
Câu 1:
Hàm số y=x−2x−1y=x−2x−1 có đồ thị là hình vẽ nào sau đây?
A.
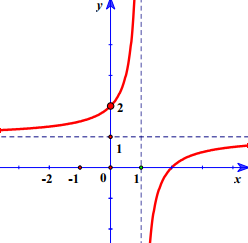
B.
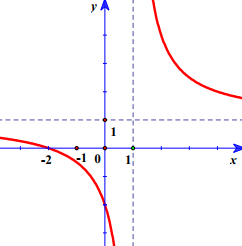
C.

D.

-
Câu 2:
Bất phương trình √2x3+3x2+6x+16−√4−x≥2√3√2x3+3x2+6x+16−√4−x≥2√3 có tập nghiệm là [a;b][a;b] . Hỏi tổng a + b có giá trị là bao nhiêu?
A. -2
B. 4
C. 5
D. 3
-
Câu 3:
Tìm giá trị lớn nhất của tham số m sao cho bất phương trình 2cos2x+3sin2x≥m⋅3cos2x2cos2x+3sin2x≥m⋅3cos2x có nghiệm?
A. m=4
B. m=8
C. m=12
D. m=16
-
Câu 4:
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình: −x3+3mx−2<−1x3−x3+3mx−2<−1x3 nghiệm đúng ∀x≥1?∀x≥1?
A. m<23m<23
B. m≥23m≥23
C. m≥32m≥32
D. −13≤m≤32−13≤m≤32
-
Câu 5:
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình m⋅4x+(m−1)⋅2x+2+m−1>0m⋅4x+(m−1)⋅2x+2+m−1>0 nghiệm đúng ∀x∈R?
A. m≤3
B. m≥1
C. −1≤m≤4
D. m≥0
-
Câu 6:
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình √3+x+√6−x−√18+3x−x2≤m2−m+1 nghiệm đúng ∀x∈[−3,6]?
A. m≥−1
B. −1≤m≤0
C. 0≤m≤2
D. m≤−1hoặcm≥2
-
Câu 7:
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 3(√1+x+√3−x)−2√(1+x)(3−x)≥m nghiệm đúng với mọi x∈[−1;3]?
A. m≤6
B. m≥6
C. m≥6√2−4
D. m≤6√2−4
-
Câu 8:
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình √(1+2x)(3−x)>m+2x2−5x−3 nghiệm đúng với mọi x∈[−12;3]?
A. m>1
B. m>0
C. m<1
D. m<0
-
Câu 9:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình 3√x−1+m√x+1=24√x2−1 có hai nghiệm thực?
A. 13≤m<1
B. −1≤m≤14
C. −2<m≤13
D. 0≤m<13
-
Câu 10:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình √x2+mx+2=2x+1 có hai nghiệm thực?
A. m≥−72
B. m≥32
C. m≥92
D. ∀m∈R
-
Câu 11:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình: log23x+√log23x+1−2m−1=0 có ít nhất một nghiệm trên đoạn [1;3√3]?
A. −1≤m≤3
B. 0≤m≤2
C. 0≤m≤3
D. −1≤m≤2
-
Câu 12:
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình x2−3x+2≤0 cũng là nghiệm của bất phương trình mx2+(m+1)x+m+1≥0?
A. m≤−1
B. m≤−47
C. m≥−47
D. m≥−1
-
Câu 13:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình √x2−4x+5=m+4x−x2 có đúng 2 nghiệm dương?
A. 1≤m≤3
B. −3<m<√5
C. −√5<m<3
D. −3≤m<3
-
Câu 14:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình 2√x+1=x+m có nghiệm thực?
A. m≥2
B. m≤2
C. m≥3
D. m≤3
-
Câu 15:
Tìm tất cả các giá trị thực k đề phương trình |−2x3−32x2+3x+12|=|k2−1| có đúng 4 nghiệm phân biệt.
A. k > 6
B. 1 < k < 2
C. - 2 < k < 6
D. k∈(−2;−34)∪(194;6)
-
Câu 16:
Cho hàm số f(x) = x3-3x2+ 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình |x|3−3x2+2 = mx3-3x2+2 = m có nhiều nghiệm thực nhất
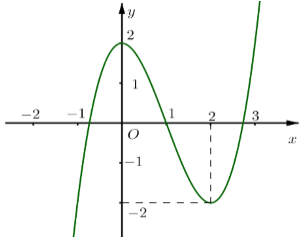
A. m > - 2
B. m > 0
C. - 2 < m < 2
D. m < 2
-
Câu 17:
Cho hàm số y = f(x) xác định trên R và có đồ thị như hình bên. Hỏi phương trình f(|x-2|) = −12 có bao nhiêu nghiệm?
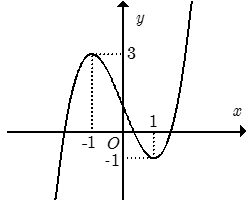
A. 2
B. 0
C. 6
D. 4
-
Câu 18:
Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số y=x|x−1| ?
A.
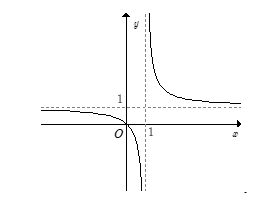
B.
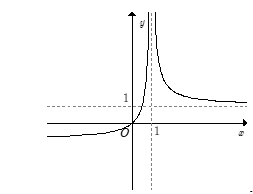
C.
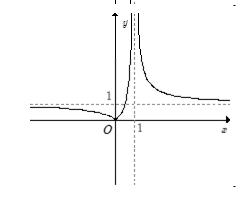
D.
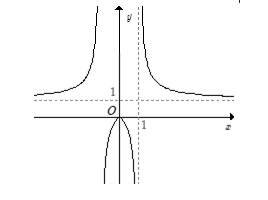
-
Câu 19:
Cho hàm số y=ax+bcx+d(a,b,c,d∈R,−dc≠0) đồ thị hàm số y = f’(x) như hình vẽ.
.png)
Biết đồ thị hàm số y = f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y=x−3x+1
B. y=x+3x−1
C. y=x+3x+1
D. y=x−3x−1
-
Câu 20:
Cho hàm số y = f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc toạ độ và đồ thị hàm số y = f’( x) cho bởi hình vẽ bên. Tính f( 3) –f( 1)?
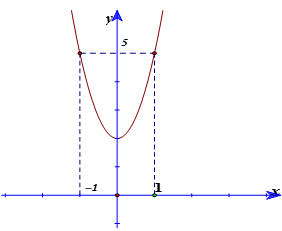
A. 24
B. 28
C. 26
D. 21
-
Câu 21:
Cho hàm số y = f(x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị hàm số y = f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ?
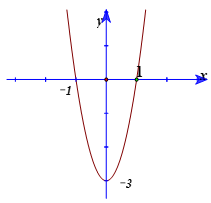
A. y = x3-3x+2.
B. y = x3+3x+2.
C. y = x3-2x+2.
D. y = x3-3x-1.
-
Câu 22:
Cho hàm số y = x3-6x2+9x-1 có đồ thị là (C) . Từ một điểm bất kì trên đường thẳng x = 2 kẻ được bao nhiêu tiếp tuyến đến (C)
A. 2
B. 1
C. 3
D. 0
-
Câu 23:
Qua điểm A( 0;2 ) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x4-2x2+2?
A. 1
B. 2
C. 3
D. 4
-
Câu 24:
Cho hàm số y = 3x-4x3 có đồ thị (C). Từ điểm M(1;3) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số (C) ?
A. 0
B. 3
C. 2
D. 1
-
Câu 25:
Viết phương trình tiếp tuyến d của đồ thị (C) : y=2x+1x+1 biết d cách đều điểm A( 2; 4) và B( -4; -2).
A. y=14x+14,y=x+3,y=x+1
B. y=14x+52,y=x+5,y=x+1
C. y=14x+54,y=x+4,y=x+1
D. y=14x+54,y=x+5,y=x+1
-
Câu 26:
Cho hàm số y=2x+1x−1 có đồ thị (C). Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến của (C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách lớn nhất từ gốc tọa độ đến tiếp tuyến Δ gần giá trị nào nhất?
A. 6
B. 4
C. 3
D. 5
-
Câu 27:
Cho hàm số y=2x−1x−1 có đồ thị (C) và điểm I (1; 2). Điểm M( a; b) ; a > 0 thuộc (C) sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM. Giá trị a+ b bằng?
A. 3
B. 4
C. 5
D. 6
-
Câu 28:
Cho hàm số y=x−abx+c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A = a+ b+ c
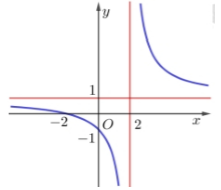
A. - 2
B. - 3
C. - 4
D. - 5
-
Câu 29:
Cho hàm số y=x+22x+3(1). Viết phương trình tiếp tuyến của đồ thị hàm số đã cho, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB cân tại gốc tọa độ.
A. y = -x+1
B. y = - x
C. y = -x- 1
D. y = -x- 2
-
Câu 30:
Cho hàm số y=2x−1x−1 có đồ thị là (C) . Gọi I là giao điểm hai tiệm cận của (C) . tồn tại điểm M( a; b) với; a; b nguyên dương thuộc (C) có hoành độ lớn hơn 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng MI. Khi đó b-a = ?
A. 0
B. - 1
C. 2
D. 1
-
Câu 31:
Cho hàm số y = x4- 2mx2+m (1) với m là tham số thực. Gọi (C) là đồ thị hàm số (1); d là tiếp tuyến của (C) tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm B( 3/4; 1) đến đường thẳng d đạt giá trị lớn nhất?
A. 0
B. 1
C. 2
D. 3
-
Câu 32:
Cho hàm số y = x3- x2+ x + 1 có đồ thị ( C) . Tiếp tuyến tại điểm N( x; y) của (C) cắt đồ thị (C) tại điểm thứ hai là M( -1; -2). Khi đó x+ y = ?
A. 1
B. 2
C. 3
D. 4
-
Câu 33:
Cho hàm số y = x3- 3mx2+ 3( m+1) x+1 (1) với m là tham số. Gọi (C) là đồ thị hàm số (1) và K là điểm thuộc (C) có hoành độ bằng -1. Tìm tất cả các giá trị của tham số m để tiếp tuyến của ( C) tại điểm K song song với đường thẳng d: 3x+ y = 0 là
A. 1
B. 2
C. 3
D. Không có giá trị nào của m thỏa mãn
-
Câu 34:
Cho hàm số y = x3- 3x2-m- 1 có đồ thị ( C) . Giá trị của tham số m để đồ thị C cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là
A. m = 1
B. m = - 1
C. m = - 3
D. m = 3
-
Câu 35:
Tìm tất cả các giá trị thực của tham số m để đường thẳng y = - mx cắt đồ thị của hàm số y = x3- 3x2-m+ 2 tại ba điểm phân biệt A; B; C sao cho AB = BC.
A. m < 1
B. m > 2
C. m < 3
D. m > 4
-
Câu 36:
Cho hàm số y=2x+1x+1 có đồ thị C và d: y= x+ m. Giá trị của tham số m để d cắt C tại hai điểm phân biệt A; B sao cho tiếp tuyến tại A và B song song với nhau.
A. m = 6
B. m = 0
C. m = - 3
D. Đáp án khác
-
Câu 37:
Cho đồ thị C: y = 2x3-3x2-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k để C cắt d tại ba điểm phân biệt là
A. {k<98k≠0
B. {k>−98k≠0
C. {k<−98k≠0
D. {k>98k≠0
-
Câu 38:
Gọi d là đường thẳng đi qua điểm A( -1; 0) với hệ số góc k. Tìm k để đường thẳng d cắt đồ thị hàm số C: y = x3-3x2+ 4 tại ba điểm phân biệt A; B; C và tam giác OBC có diện tích bằng 1?
A. k = 2
B. k = - 1
C. k = 1
D. Đáp án khác
-
Câu 39:
Cho hàm số y= f( x) = ax4+ bx3+ cx2+ dx+ e và hàm số y = f’( x) có đồ thị như hình vẽ bên. Biết f( b) < 0 , hỏi đồ thị hàm số y = f(x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
.png)
A. 1
B. 2
C. 3
D. 4
-
Câu 40:
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C). Đường thẳng d: y = - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2√7 là
A. m = - 1
B. m = - 1 hoặc m = 4
C. m = 4
D. Không tồn tại m
-
Câu 41:
Cho hàm số y = x3-3x2-m-1 có đồ thị (C). Giá trị của tham số m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là
A. m = 0
B. m = 3
C. m = - 3
D. m=±6
-
Câu 42:
Cho hàm số y = x3-3x2+4 có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k . Có bao nhiêu giá trị nguyên của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
A. 4
B. 1
C. 6
D. Vô số
-
Câu 43:
Cho phương trình x3 - 3x2 + 1 - m = 0 (1). Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa x1 < 1 < x2 < x3 khi
A. m = - 1
B. -1 < m < 3
C. -3 < m < -1
D. Đáp án khác
-
Câu 44:
Cho hàm số y=mx−1x+2 có đồ thị là (C) . Tìm m để đường thẳng d: y = 2x-1 cắt đồ thị (C) tại hai điểm phân biệt A; B sao cho AB = √10
A. m = 2
B. m = 3
C. m = 1
D. m = 4
-
Câu 45:
Tìm m để đồ thị hàm số y = x3+mx+2 cắt trục hoành tại một điểm duy nhất.
A. m > 1
B. m > 2
C. m > - 3
D. m < - 2
-
Câu 46:
Cho hàm số y = 2x3 - 3x2 + 1 có đồ thị và đường thẳng d: y = x - 1. Giao điểm của (C) và d lần lượt là A(1; 0); B và C. Khi đó khoảng cách giữa B và C là
A. BC=√302
B. BC=√342
C. BC=3√22
D. BC=√142
-
Câu 47:
Cho hàm số y= f(x) = ax3+ bx2+cx+d có đạo hàm là hàm số y = f’ (x) với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y = f( x) cắt trục tung tại điểm có tung độ là bao nhiêu?
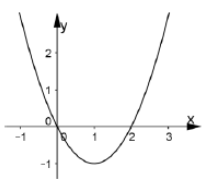
A. 23
B. 1
C. 32
D. 43
-
Câu 48:
Tìm giá trị của tham số m để đồ thị hàm số y = x3 – 3x + 2m đi qua điểm A(-1;6)
A. m = 3
B. m = - 3
C. m = - 2
D. m = 2
-
Câu 49:
Đồ thị của hàm số y = - x3 + 3x2 + 2x – 1 và đồ thị của hàm số y = 3x2 – 2x – 1 có tất cả bao nhiêu điểm chung
A. 1
B. 3
C. 2
D. 0
-
Câu 50:
Tọa độ giao điểm có hoành độ nhỏ hơn 1 của đường (C): y=3x−1x−1 và đường thẳng (d): y = x + 1 là:
A. A(0;-1).
B. A(0;1).
C. A(-1;2).
D. A(-2;7).














