ADMICRO
Tìm m để đồ thị hàm số y = x3+mx+2 cắt trục hoành tại một điểm duy nhất.
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
ZUNIA12
Lời giải:
Báo saiPhương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là x3+mx+2=0x3+mx+2=0
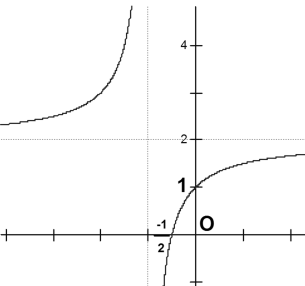
Vì x = 0 không là nghiệm của phương trình, nên phương trình tương đương với m=−x2−2xm=−x2−2x
Xét hàm số:
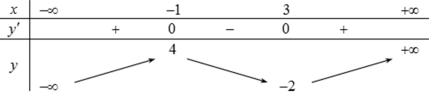
f(x)=−x2−2x,x≠0,⇒f′(x)=−2x+2x2=−2x3+2x2f′(x)=0⇔x=1
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy đồ thị cắt trục hoành tại một điểm duy nhất khi và chỉ khi m > -3.
Vậy m> -3 thỏa yêu cầu bài toán.
ZUNIA9
AANETWORK