Câu hỏi:
Listen to two friends talking about movies. Fill in the blanks with suitable words.
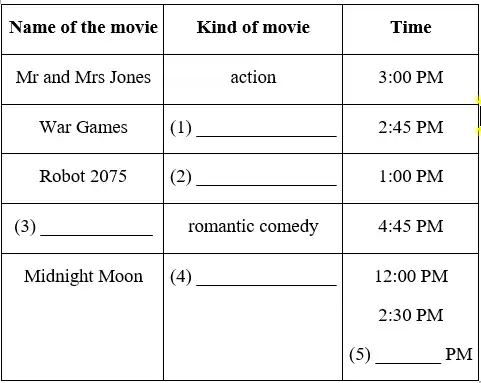
-> Write the answer for number (5)
Đáp án đúng: 7:30
Giải thích: Thời gian vào buổi chiều-tối của phim Midnight Moon: _____
Thông tin: Mario: Is it on this evening?
Tamara: Yes, at 7:30.
Tạm dịch: Mario: Có chiếu vào buổi tối không?
Tamara: Có, lúc 7:30.
Đáp án 7:30.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Giữa Học Kì I - Tiếng Anh 7 - i-Learn Smart World - Bộ Đề 01 được thiết kế chi tiết nhằm đánh giá đầy đủ các kỹ năng của học sinh trong quá trình học Tiếng Anh. Đề thi bao gồm các phần như nghe hiểu, phát âm, từ vựng, ngữ pháp, đọc hiểu và viết, với các câu hỏi đa dạng từ nhận biết, thông hiểu đến vận dụng.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026
