525 câu trắc nghiệm môn Toán rời rạc kèm lời giải chi tiết - Phần 4
30 câu hỏi 60 phút
Có bao nhiêu số nguyên dương không lớn hơn 1000 không chia hết cho 7 hoặc 11.
220
780
768
1768
Gọi A là tập hợp các số nguyên dương không lớn hơn 1000 chia hết cho 7, B là tập hợp các số nguyên dương không lớn hơn 1000 chia hết cho 11.
Số các số chia hết cho 7 là: |A| = ⌊1000/7⌋ = 142.
Số các số chia hết cho 11 là: |B| = ⌊1000/11⌋ = 90.
Số các số chia hết cho cả 7 và 11 (tức là chia hết cho 77) là: |A ∩ B| = ⌊1000/77⌋ = 12.
Số các số chia hết cho 7 hoặc 11 là: |A ∪ B| = |A| + |B| - |A ∩ B| = 142 + 90 - 12 = 220.
Vậy, số các số nguyên dương không lớn hơn 1000 không chia hết cho 7 hoặc 11 là: 1000 - |A ∪ B| = 1000 - 220 = 780.
Danh sách câu hỏi:
Gọi A là tập hợp các số nguyên dương không lớn hơn 1000 chia hết cho 7, B là tập hợp các số nguyên dương không lớn hơn 1000 chia hết cho 11.
Số các số chia hết cho 7 là: |A| = ⌊1000/7⌋ = 142.
Số các số chia hết cho 11 là: |B| = ⌊1000/11⌋ = 90.
Số các số chia hết cho cả 7 và 11 (tức là chia hết cho 77) là: |A ∩ B| = ⌊1000/77⌋ = 12.
Số các số chia hết cho 7 hoặc 11 là: |A ∪ B| = |A| + |B| - |A ∩ B| = 142 + 90 - 12 = 220.
Vậy, số các số nguyên dương không lớn hơn 1000 không chia hết cho 7 hoặc 11 là: 1000 - |A ∪ B| = 1000 - 220 = 780.
Xâu nhị phân độ dài 10 bắt đầu bằng 11 và kết thúc bằng 00 có dạng 11xxxxxx00. Có 6 vị trí (xxxxxx) có thể là 0 hoặc 1. Mỗi vị trí có 2 lựa chọn (0 hoặc 1). Vì vậy, có 26 = 64 xâu nhị phân thỏa mãn điều kiện.
Để tính số phần tử của hợp của ba tập hợp A1, A2, và A3, ta sử dụng công thức:
|A1 ∪ A2 ∪ A3| = |A1| + |A2| + |A3| - |A1 ∩ A2| - |A1 ∩ A3| - |A2 ∩ A3| + |A1 ∩ A2 ∩ A3|
Trong đó:
- |A1|, |A2|, |A3| là số phần tử của mỗi tập hợp.
- |A1 ∩ A2|, |A1 ∩ A3|, |A2 ∩ A3| là số phần tử chung của mỗi cặp hai tập hợp.
- |A1 ∩ A2 ∩ A3| là số phần tử chung của cả ba tập hợp.
Theo đề bài, ta có:
- |A1| = |A2| = |A3| = 100
- |A1 ∩ A2| = |A1 ∩ A3| = |A2 ∩ A3| = 50
- |A1 ∩ A2 ∩ A3| = 10
Thay các giá trị này vào công thức, ta được:
|A1 ∪ A2 ∪ A3| = 100 + 100 + 100 - 50 - 50 - 50 + 10 = 300 - 150 + 10 = 160
Vậy số phần tử của A1 ∪ A2 ∪ A3 là 160.
Câu 24:
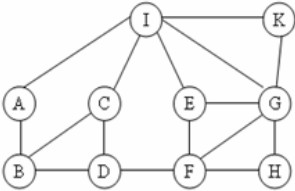
Cho mạng G, điểm phát s điểm thu t. Tính cân bằng của luồng f trên mạng G phải thỏa mãn cho:
.jpg)