Trắc nghiệm Ba đường conic Toán Lớp 10

Câu 1:

Cho elip \(\left( E \right):\,\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\). Khẳng định nào sau đây ĐÚNG?

Câu 2:

Dọc theo bờ biển, người ta thiết lập hệ thống định vị vô tuyến dẫn đường tầm xa để truyền tín hiệu cho máy bay hoặc tàu thuỷ hoạt động trên biển. Trong hệ thống đó có hai đài vô tuyến đặt lần lượt tại địa điểm A và địa điểm B, khoảng cách AB = 650 km (Hình 18). Giả sử có một con tàu chuyển động trên biển với quỹ đạo là hypebol nhận A và B là hai tiêu điểm.

Khi đang ở vị trí P, máy thu tín hiệu trên con tàu chuyển đổi chênh lệch thời gian nhận các tín hiệu từ A và B thành hiệu khoảng cách |P_A – P_B|. Giả sử thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A là 0,0012 s. Vận tốc di chuyển của tín hiệu là 3 . 10⁸ m/s. Thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A luôn là

Câu 3:

Dọc theo bờ biển, người ta thiết lập hệ thống định vị vô tuyến dẫn đường tầm xa để truyền tín hiệu cho máy bay hoặc tàu thuỷ hoạt động trên biển. Trong hệ thống đó có hai đài vô tuyến đặt lần lượt tại địa điểm A và địa điểm B, khoảng cách AB = 650 km (Hình 18). Giả sử có một con tàu chuyển động trên biển với quỹ đạo là hypebol nhận A và B là hai tiêu điểm.

Khi đang ở vị trí P, máy thu tín hiệu trên con tàu chuyển đổi chênh lệch thời gian nhận các tín hiệu từ A và B thành hiệu khoảng cách |P_A – P_B|. Giả sử thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A là 0,0012 s. Vận tốc di chuyển của tín hiệu là 3 . 10⁸ m/s. Phương trình hypebol mô tả quỹ đạo chuyển động của con tàu là:

Câu 4:

Trong mặt phẳng tọa độ Oxy, cho hypebol \(\left( H \right):\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\). Lập phương trình chính tắc của elip (E), biết rằng (E) có các tiêu điểm là các tiêu điểm của (H) và các đỉnh của hình chữ nhật cơ sở của (H) đều nằm trên (E).

Câu 5:

Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc là x² – y² = 1. Kết luận mối quan hệ hai đường tiệm cận của hypebol nào sau đây đúng?

Câu 6:

Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{1} = 1\). Xác định phương trình các đường tiệm cận của hypebol và vẽ hypebol trên?

Câu 7:

Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{1} = 1\). Toạ độ các đỉnh, tiêu điểm, tiêu cự của hypebol lần lượt là:

Câu 8:

Viết phương trình chính tắc của hypebol, tiêu điểm F₂ (4; 0) và phương trình một đường tiệm cận là \(y = - \frac{{\sqrt 7 }}{3}x\)

Câu 9:

Viết phương trình chính tắc của hypebol, đỉnh là A₂(4; 0) và tiêu cự bằng 10:

Câu 10:

Viết phương trình chính tắc của hypebol, biết tiêu điểm là F₁(– 3; 0) và đỉnh là A₂ (2; 0).

Câu 11:

Cho hypebol (H) có một đỉnh là A1(–4; 0) và tiêu cự là 10. Viết phương trình chính tắc và vẽ hypebol (H).

Câu 12:

Để vẽ hypebol (H) bạn An đã thực hiện các bước như sau:

Vẽ hypebol (H) với a = 3, b = 4. (H) có các đỉnh là A₁(– 3; 0), A₂(3; 0).

Bước 1. Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn đường thẳng x = –3, x = 3, y = – 4, y = 4.

Bước 2. Vẽ hai đường chéo của hình chữ nhật cơ sở.

Tim một số điểm cụ thể thuộc hypebol, chẳng hạn ta thấy điểm\(M\left( {5;\frac{{16}}{3}} \right)\) thuộc (H). Do đó các điểm\({M_1}\left( {5; - \frac{{16}}{3}} \right),{M_2}\left( { - 5;\frac{{16}}{3}} \right),{M_3}\left( { - 5; - \frac{{16}}{3}} \right)\) thuộc (H).

Bước 3. Vẽ đường hypebol bên ngoài hình chữ nhật cơ sở; nhánh bên trái tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm A₁(– 3; 0) và đi qua M₂, M₃; nhánh bên phải tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm A₂(3; 0) và đi qua M, M₁. Vẽ các điểm thuộc hypebol càng xa gốc toạ độ thi càng sát với đường tiệm cận. Hypebol nhận gốc toạ độ là tâm đối xứng và hai trục toạ độ là hai trục đối xứng.

Bằng cách này, em hãy cho biết bạn An đã vẽ được  hypebol (H) có phương trình như thế nào?

Câu 13:

Tìm các tiêu điểm và đường chuẩn của hypebol có phương trình chính tắc là \(\frac{{{x^2}}}{{11}} - \frac{{{y^2}}}{{25}} = 1.\)

Câu 14:

Hoạt động 7 trang 53 Chuyên đề Toán 10: Cho hypebol (H) có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)với a > 0, b > 0. Xét đường thẳng \({\Delta _1}:x = - \frac{a}{e}\)

Với mỗi điểm M (x₀; y₀) ∈ (H) (Hình 17), tính:

a) Khoảng cách d (M, Δ₁) từ điểm M(x₀; y₀) đến đường thẳng Δ₁.

Câu 15:

Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{{144}} - \frac{{{y^2}}}{{25}} = 1.\). Giả sử M là điểm thuộc hypebol có hoành độ là 15. Tìm độ dài các bán kính qua tiêu của điểm M.

Câu 16:

Trong mặt phẳng, xét đường hypebol (H) là tập hợp các điểm M sao cho |MF₁ – MF₂| = 2a, ở đó F₁F₂ = 2c với c > a > 0. Ta chọn hệ trục toạ độ Oxy có gốc là trung điểm của đoạn thẳng F₁F₂. Trục Oy là đường trung trực của F₁F₂ và F₂ nằm trên tia Ox (Hình 16). Khi đó F₁(c; 0), F₂(c; 0) là các tiêu điểm của (H).

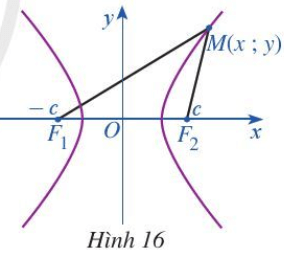
Với mỗi điểm M(x; y) thuộc đường hypebol (H). Tính MF₂² theo x, y ta được:

Câu 17:

Trong mặt phẳng, xét đường hypebol (H) là tập hợp các điểm M sao cho |MF₁ – MF₂| = 2a, ở đó F₁F₂ = 2c với c > a > 0. Ta chọn hệ trục toạ độ Oxy có gốc là trung điểm của đoạn thẳng F₁F₂. Trục Oy là đường trung trực của F₁F₂ và F₂ nằm trên tia Ox (Hình 16). Khi đó F₁(c; 0), F₂(c; 0) là các tiêu điểm của (H).

Với mỗi điểm M(x; y) thuộc đường hypebol (H). Tính MF₁² theo x, y ta được:

Câu 18:

Viết phương trình chính tắc của hypebol, biết độ dài trục ảo bằng 6 và tâm sai bằng \(\frac{5}{4}\)?

Câu 19:

Phương trình chính tắc của hypebol có một đỉnh là A2(5; 0) và một đường tiệm cận là y = –3x là:

Câu 20:

Cho  hypebol (H) (Hình 15). Phương trình hai đường thẳng PR và QS lần lượt là:

Câu 21:

Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó a > 0, b > 0 (Hình 14).

Cho điểm M(x; y) nằm trên hypebol (H). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc O. Vị trí các điểm M1, M2, M3 so với hypebol (H)

Câu 22:

Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó a > 0, b > 0 (Hình 13).

Hypebol (H) cắt trục Ox tại các điểm A₁, A₂. Tìm độ dài các đoạn thẳng OA₁ và OA₂

Câu 23:

Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), trong đó a > 0, b > 0 (Hình 13).

Tìm toạ độ hai tiêu điểm F1, F2 của hypebol (H)

Câu 24:

Các vật liệu xây dựng đều có hệ số dãn nở. Vì thế, khi đặt dầm cầu, người ta thường đặt cố định một đầu dầm, đầu còn lại đặt trên một con lăn có thể di động được nhằm giải quyết sự dãn nở của vật liệu. Hình 21 minh hoạ một dầm cầu được đặt ở hai bờ kênh, giới hạn bởi hai cung parabol có cùng trục đối xúmg. Người ta thiết kế các thanh giằng nối hai cung parabol đó sao cho các thanh giằng theo phương thẳng đứng cách đều nhau và cách đều hai đầu dầm.

Tính tổng độ dài của các thanh giằng theo phương thẳng đứng.

Câu 25:

Trong mặt phẳng tọa độ Oxy, cho parabol có phương trình chính tắc y² = 8x. Xác định tọa độ tiêu điểm và phương trình đường chuẩn của parabol.

Câu 26:

Phương trình chính tắc của parabol đi qua điểm A(4; 9):

Câu 27:

Phương trình chính tắc của parabol có phương trình đường chuẩn là x = –4:

Câu 28:

Phương trình chính tắc của parabol có tiêu điểm là F2(5; 0) là:

Câu 29:

Parabol y² = 2px biết tiêu điểm của parabol là \(F\left( {\frac{1}{4};0} \right).\) Viết phương trình của parabol?

Câu 30:

Cho (P) :  y² = 8x. Tìm toạ độ điểm M thuộc parabol (P), biết khoảng cách từ M đến tiêu điểm bằng 6?

Câu 31:

 Lập phương trình chính tắc của parabol (P), biết phương trình đường chuẩn là x = –2.

Câu 32:

Trong mặt phẳng toạ độ Oxy, ta xét parabol (P) có phương trình chính tắc là y2 = 2px (p > 0) (Hình 20).

Độ dài đoạn thẳng MK; MF là:

Câu 33:

Trong mặt phẳng toạ độ Oxy, ta xét parabol (P) có phương trình chính tắc là y² = 2px (p > 0) (Hình 20).

So sánh khoảng cách MF từ điểm M đến tiêu điểm F và khoảng cách MK từ điểm M đến đường chuẩn Δ ta được kết luận:

Câu 34:

Trong mặt phẳng tọa độ Oxy, ta xét parabol (P) có phương trình chính tắc y² = 2px (p > 0) (Hình 19).

Cho điểm M(x; y) nằm trên parabol (P). Gọi M1 là điểm đối xứng của M qua trục Ox.  Xác định điểm M₁

Câu 35:

Trong mặt phẳng tọa độ Oxy, ta xét parabol (P) có phương trình chính tắc y² = 2px (p > 0) (Hình 19).

Toạ độ điểm H và viết phương trình đường chuẩn Δ của parabol (P) là:

Câu 36:

Trong mặt phẳng tọa độ Oxy, ta xét parabol (P) có phương trình chính tắc y² = 2px (p > 0) (Hình 19).

Toạ độ tiêu điểm F của parabol (P) bằng:

Câu 37:

Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39).

Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên Δ. MK² – MO² = 1 khi đó:

Câu 38:

Sao Diêm Vương chuyển động xung quanh Mặt Trời theo quỹ đạo là một đường elip có một trong hai tiêu điểm là tâm của Mặt Trời. Biết elip này có bán trục lớn a ≈ 5,906 . 106 km và tâm sai e ≈ 0,249. (Nguồn: https://vi.wikipedia.org) Tìm khoảng cách nhỏ nhất (gần đúng) giữa Sao Diêm Vương và Mặt Trời.

Câu 39:

Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là một đường elip nhận tâm Trái Đất là một tiêu điểm. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm (1 dặm xấp xỉ 1,609 km). Tìm tâm sai của quỹ đạo đó, biết bán kính của Trái Đất xấp xỉ 4000 dặm. (Nguồn: Sách giáo khoa Hình học 10, Ban Nâng cao, Nhà xuất bản Giảo dục Việt Nam, 2018)

Câu 40:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x = –5 và điểm F(–4; 0). Cho ba điểm A(–3; 1), B(2; 8), C(0; 3). Mỗi điểm A, B, C lần lượt nằm trên loại đường conic nào nhận F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm đó?

Câu 41:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x = –5 và điểm F(–4; 0). Cho ba điểm A(–3; 1), B(2; 8), C(0; 3). Tính các tỉ số sau: \(\frac{{{\rm{AF}}}}{{d(A,\Delta )}};\frac{{{\rm{BF}}}}{{d(B,\Delta )}};\frac{{{\rm{CF}}}}{{d(C,\Delta )}}\) ta được kết quả lần lượt là:

Câu 42:

Cho parabol có phương trình chính tắc y² = 2x. Tìm tiêu điểm, phương trình đường chuẩn của parabol?

Câu 43:

Cho đường conic có phương trình \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{64}} = 1\) Độ dài các trục, toạ độ tiêu điểm, tiêu cự, tâm sai của các đường conic đó lần lượt là:

Câu 44:

Cho đường conic có phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\) Độ dài các trục, toạ độ tiêu điểm, tiêu cự, tâm sai của các đường conic đó lần lượt là:

Câu 45:

Quan sát Hình 22a, Hình 22b, Hình 22c, tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó lần lượt theo a, b, c là:

Câu 46:

Hình 11 minh hoạ mặt cắt đứng của một căn phòng trong bảo tàng với mái vòm trần nhà của căn phòng đó có dạng một nửa đường elip. Chiều rộng của căn phòng là 16 m, chiều cao của tượng là 4 m, chiều cao của mái vòm là 3 m.

Một nguồn sáng được đặt tại tiêu điểm thứ nhất của elip. Cần đặt bức tượng ở vị tri có toạ độ nào để bức tượng sáng rõ nhất? Giả thiết rằng vòm trần phản xạ ánh sáng. Biết rằng, một tia sáng xuất phát từ một tiêu điểm của elip, sau khi phản xạ tại elip thi sẽ đi qua tiêu điểm còn lại.

Câu 47:

Hình 11 minh hoạ mặt cắt đứng của một căn phòng trong bảo tàng với mái vòm trần nhà của căn phòng đó có dạng một nửa đường elip. Chiều rộng của căn phòng là 16 m, chiều cao của tượng là 4 m, chiều cao của mái vòm là 3 m.

Phương trình chính tắc của elip biểu diễn mái vòm trần nhà trong hệ trục tọa độ Oxy (đơn vị trên hai trục là mét) là:

Câu 48:

Cho elip (E):  \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\). Tìm toạ độ điểm M ∈ (E) sao cho độ dài F₂M lớn nhất, biết F₂ là một tiêu điểm có hoành độ dương của (E).

Câu 49:

Elip với độ dài hai trục là 20 và 12 có phương trình chính tắc là: 

Câu 50:

Phương trình chính tắc của parabol có tiêu điểm \(\left( {2;0} \right)\) là: