Trắc nghiệm Sự đồng biến, nghịch biến của hàm số Toán Lớp 12
-
Câu 1:
Hàm số y = 2x3-9x2+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình \(2{\left| x \right|^3} - 9{x^{2\;}}\; + \;12\left| x \right|\; + \;m\; = \;0\) có sáu nghiệm phân biệt.
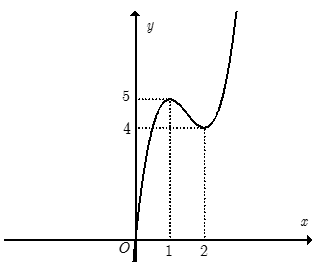
A. m < - 5
B. - 5 < m < - 4
C. 4 < m < 5
D. m > - 4
-
Câu 2:
Cho hàm số y = f(x) có đạo hàm trên R thoả f( 2) = f( -2) = 0 và đồ thị của hàm số y = f’ (x) có dạng như hình bên. Hàm số y = (f( x)) 2 nghịch biến trên khoảng nào trong các khoảng sau ?
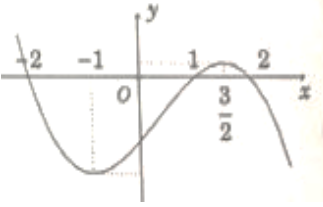
A. \(\left( { - 1;\frac{3}{2}} \right)\)
B. (-1; 1)
C. (-2; -1)
D. (1; 2)
-
Câu 3:
Cho hàm số y = f(x). Biết f(x) có đạo hàm f’(x) và hàm số y = f’(x) có đồ thị như hình vẽ. Đặt g(x) = f(x+1). Kết luận nào sau đây đúng?
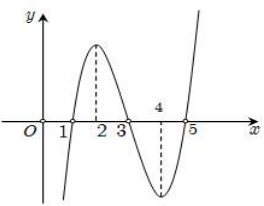
A. Hàm số g( x) có hai điểm cực trị.
B. Hàm số g(x) đồng biến trên khoảng (1; 3).
C. Hàm số g(x) nghịch biến trên khoảng (2; 4).
D. Hàm số g(x) có hai điểm cực đại và một điểm cực tiểu
-
Câu 4:
Bất phương trình \(\sqrt {{x^2} - 2x + 3} - \sqrt {{x^2} - 6x + 11} > \sqrt {3 - x} - \sqrt {x - 1} \) có tập nghiệm (a; b]. Hỏi hiệu b-a có giá trị là bao nhiêu?
A. 1
B. 2
C. 3
D. - 1
-
Câu 5:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(\sqrt {{x^2} + mx + 2} = 2x + 1\) có hai nghiệm thực?
A. \(m \ge - \frac{7}{2}\)
B. \(m \ge \frac{3}{2}\)
C. \(m \ge \frac{9}{2}\)
D. Với mọi m
-
Câu 6:
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2-3x+2 ≤ 0 cũng là nghiệm của bất phương trình mx2+(m+1) x+m+1 ≥ 0.
A. \(m \le - 1\)
B. \(m \le - \frac{4}{7}\)
C. \(m \ge - \frac{4}{7}\)
D. \(m \ge -1\)
-
Câu 7:
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số \(y = \ln \left( {{x^2} + 1} \right) - mx + 1\) đồng biến trên khoảng ( -∞; +∞).
A. \(\left( { - \infty ; - 1} \right]\)
B. \(\left( { - \infty ; - 1} \right)\)
C. \([-1;1]\)
D. Đáp án khác
-
Câu 8:
Tìm mối liên hệ giữa các tham số a và b sao cho hàm số y = f(x) = 2x+a.sinx+b.cosx luôn tăng trên R?
A. \(\frac{1}{a} + \frac{1}{b} = 1\)
B. \(a + 2b = 2\sqrt 3 \)
C. \({a^2} + {b^2} \le 4\)
D. \(a + 2b \ge \frac{{1 + \sqrt 2 }}{3}\)
-
Câu 9:
Tìm tất cả các giá trị thực của tham số α và β sao cho hàm số sau luôn giảm trên R?
\(y = f\left( x \right) = \frac{{ - {x^3}}}{3} + \frac{1}{2}\left( {\sin \alpha + \cos \alpha } \right){x^2} - \frac{3}{2}x\sin \alpha \cos \alpha - \sqrt {\beta - 2} \)
A. \(\frac{{\rm{\pi }}}{{12}} + k{\rm{\pi }} \le {\rm{\alpha }} \le \frac{{\rm{\pi }}}{4} + k{\rm{\pi }},\;{\rm{k}} \in Z\;,{\rm{\beta }} \ge 2.\)
B. \(\frac{\pi }{{12}} + k\pi \le \alpha \le \frac{{5\pi }}{{12}} + k\pi ,\;k \in Z\;,\beta \ge 2.\)
C. \(\alpha \le \frac{{\rm{\pi }}}{4} + k{\rm{\pi }},\;{\rm{k}} \in Z\;,{\rm{\beta }} \ge 2.\)
D. \(\alpha \ge \frac{{5\pi }}{{12}} + k\pi ,\;k \in Z\;,\beta \ge 2.\)
-
Câu 10:
Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số \(y = \frac{{2{x^2} + \left( {1 - m} \right)x + 1 + m}}{{x - m}}\) đồng biến trên khoảng (1;+∞)?
A. 3
B. 1
C. 2
D. 0
-
Câu 11:
Có bao nhiêu giá trị nguyên dương của m để hàm số y = 3x+ m(sinx+ cosx+m) đồng biến trên R ?
A. 5
B. 4
C. 3
D. 2
-
Câu 12:
Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y = {x^3} + mx - \frac{1}{{5{x^5}}}\) đồng biến với x > 0?
A. 4
B. 5
C. 3
D. 2
-
Câu 13:
Hỏi phương trình 3x2- 6x+ ln( x+1) 3+1 = 0 có bao nhiêu nghiệm phân biệt?
A. 2
B. 1
C. 3
D. 4
-
Câu 14:
Cho phương trình x3- 3x2+ 1- m = 0 (1) . Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa mãn x1 < 1< x2 < x3 khi
A. m = - 1
B. - 1 < m < 3
C. - 3 < m < - 1
D. m > - 3
-
Câu 15:
Tìm tập hợp tất cả các giá trị của tham số thực của m để hàm số y = ln( x2+ 1) –mx+1 đồng biến trên R.
A. m > 1
B. m < 1
C. \(m\le -1\)
D. \(m\ge -1\)
-
Câu 16:
Cho hàm số \(f\left( x \right) = \frac{{{x^3}}}{3} + \left( {4 - m} \right)\frac{{{x^2}}}{2} + \left( {5 - 2m} \right)x + {m^2} + 3,\), với m là tham số thực.
Hàm số \(g\left( x \right) = \frac{{{x^2} + 4x + 5}}{{x + 2}}\) có đồ thị C và bảng biến thiên sau:.png)
Tìm m sao cho hàm số f(x) đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1
A. m > 2
B. \(\left[ \begin{array}{l} m < - 2\\ m > 2 \end{array} \right.\)
C. \(m <- \frac{5}{2}\)
D. \(m > \frac{5}{2}\)
-
Câu 17:
Với giá trị nào của tham số m thì hàm số \(y = \sin \left( x \right) - \cos \left( x \right) + 2017\sqrt 2 mx\) đồng biến trên R.
A. \(m \ge 2017\)
B. m = 1
C. \(m \ge \frac{1}{{2017}}\)
D. \(m \ge - \frac{1}{{2017}}\)
-
Câu 18:
Cho hàm số y = f( x) có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 9} \right){\left( {x - 4} \right)^2}.\). Xét hàm số y = g( x) = f(x2)
Trong các phát biểu sau; tìm số phát biểu đúng
I. Hàm số y = g( x) đồng biến trên( 3; +∞)
II. Hàm số y = g(x) nghịch biến trên( -∞; -3)
III. Hàm số y = g( x) có 5 điểm cực trị
IV. \(\mathop {min}\limits_{x \in R} \;g\left( x \right) = f\left( 9 \right)\)
A. 1
B. 2
C. 3
D. 4
-
Câu 19:
Cho hàm số y = f( x).(x-1) liên tục trên R và có đồ thị như hình vẽ.
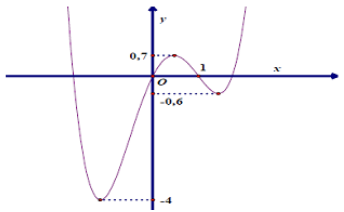
Tìm tất cả các giá trị của tham số m để phương trình f(x) : |x - 1| = m có số nghiệm lớn nhất
A. (-0,6 ; 0]
B. (-0,6 ; 0)
C. (0; 0,06)
D. (0; 0,6)
-
Câu 20:
Cho hàm số y = f(x) = x4+ 2mx2+ m. Tìm m để f(x) > 0 với mọi m.
A. m > 0
B. m < 0
C. m < 1
D. m > 1
-
Câu 21:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(3\sqrt {x - 1} + m\sqrt {x + 1} = 2\sqrt[4]{{{x^2} - 1}}\) có hai nghiệm thực?
A. \(\frac{1}{3} \le m < 1.\)
B. \( - 1 \le m < \frac{1}{4}\)
C. \( - 2 \le m < \frac{1}{3}\)
D. \(0\le m < \frac{1}{3}\)
-
Câu 22:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(\sqrt {{x^2} + mx + 2} = 2x + 1\) có hai nghiệm thực?
A. \(m\le 3\)
B. \(m\le 5\)
C. m > 1
D. Đáp án khác
-
Câu 23:
Bất phương trình \(\sqrt {{x^2} - 2x + 3} - \sqrt {{x^2} - 6x + 11} > \sqrt {3 - x} - \sqrt {x - 1} \) có tập nghiệm là ( a; b]. Hỏi 4a-b có giá trị là bao nhiêu?
A. 1
B. 3
C. 5
D. 7
-
Câu 24:
Tập nghiệm của bất phương trình: \(\sqrt {5x - 1} + \sqrt {x + 3} \ge 4\) có bao nhiêu giá trị nguyên trong ( 0; 2008]
A. 2006
B. 2001
C. 2008
D. 2007
-
Câu 25:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y = \frac{{\tan \;x - 2}}{{\tan \;x\; - \;m}}\) đồng biến trên khoảng \(\left( {0;\frac{{\rm{\pi }}}{4}} \right)\)?
A. 1 ≤ m < 2.
B. m ≤ 0
C. m > 2
D. Cả A và B đúng
-
Câu 26:
Cho phương trình: \(2{x^3} + {x^2} - 3x + 1 = 2\left( {3x - 1} \right)\sqrt {3x - 1} \)
Tính tổng các nghiệm cùa phương trình là :
A. 1
B. 2
C. 3
D. 4
-
Câu 27:
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:
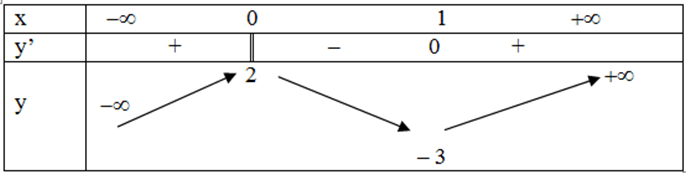
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị
B. Hàm số có giá trị cực tiểu bằng 2
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng - 3
D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1
-
Câu 28:
Cho hàm số \(y = \frac{1}{4}{x^4} - 2{x^2} + 3\). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (-2; 0) và (2; +∞)
B. Hàm số đồng biến trên khoảng (-∞; -2) và (2; +∞)
C. Hàm số nghịch biến trên khoảng (-∞; -2) và (0; 2)
D. Hàm số nghịch biến trên khoảng (-∞; 0)
-
Câu 29:
Hàm số y = x3 – 3x đồng biến trên khoảng nào?
A. (-∞; 0).
B. (-1;1).
C. (0; +∞).
D. (-∞; +∞)
-
Câu 30:
Đường cong hình bên là đồ thị của một hàm số. Hãy chọn khẳng định đúng
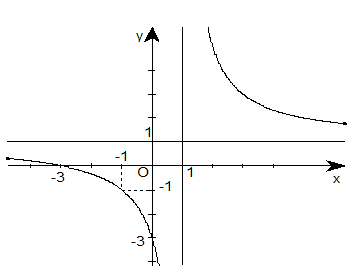
A. Hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞)
B. Hàm số nghịch biến trên R
C. Hàm số đồng biến trên R
D. Hàm số nghịch biến trên các khoảng (-∞; 1) và (1; +∞)
-
Câu 31:
Cho hàm số y = f(x) có đồ thị như hình vẽ.
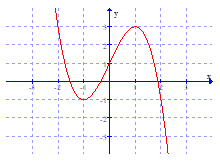
Hàm số y = f(x) đồng biến trên khoảng nào sau đây?
A. (0; +∞).
B. (-1; 1).
C. (-1; 3).
D. (1; +∞).
-
Câu 32:
Hàm số y = f(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?
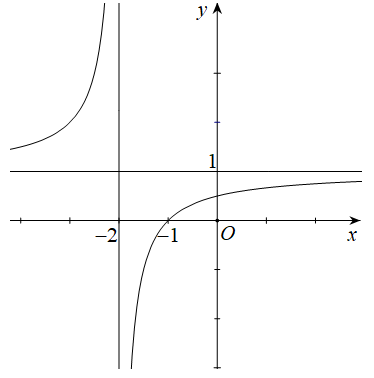
A. Đồ thị hàm số có tiệm cận đứng là x = 1 và tiệm cận ngang là y = -2.
B. Hàm số đồng biến trên các khoảng (-∞; -2), (-2; +∞).
C. Đồ thị hàm số cắt trục hoành tại điểm M(0; -1).
D. Hàm số nghịch biến trên các khoảng (-∞; -2), (-2; +∞).
-
Câu 33:
Cho hàm số y = x4 – 2x2 + 2. Kết luận nào sau đây sai?
A. Nghịch biến (-2; 2)
B. Đồng biến (2; +∞)
C. xCT = ± 2
D. yCT = - 2
-
Câu 34:
Cho hàm số y = - x3 + 3x2 – 3x + 7. Mệnh đề nào sau đây là đúng?
A. Hàm số nghịch biến trên R
B. Hàm số đồng biến trên R
C. Hàm số đạt cực đại tại x = 1
D. Hàm số đạt cực tiểu tại x = 1
-
Câu 35:
Cho hàm số \(f\left( x \right) = \frac{{{x^3}}}{3} - \frac{{{x^2}}}{2} - 6x + \frac{3}{4}\). Chọn khẳng định đúng.
A. Hàm số đồng biến trên khoảng (-2; 3).
B. Hàm số nghịch biến trên khoảng (-2; 3).
C. Hàm số nghịch biến trên (-∞; -2)
D. Hàm số đồng biến trên (-2; +∞)
-
Câu 36:
Kết luận nào sau đây về tính đơn điệu của hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) là đúng?
A. Hàm số đồng biến trên các khoảng (-∞; -1) và (-1; +∞)
B. Hàm số luôn luôn đồng biến trên R \ {-1}
C. Hàm số nghịch biến trên các khoảng (-∞; -1) và (-1; +∞)
D. Hàm số luôn luôn nghịch biến trên R \ {-1}
-
Câu 37:
Hàm số y = 2x2 – x4 nghịch biến trên những khoảng nào?
A. (-1; 0).
B. (-1; 0); (1; +∞).
C. (-∞; -1); (0; 1).
D. (-1; 1).
-
Câu 38:
Cho hàm số \(y = \frac{{ - x + 5}}{{x + 2}}\). Mệnh đề nào sau đây là đúng?
A. Hàm số nghịch biến trên mỗi khoảng (-∞; -2) và (-2; +∞)
B. Hàm số đồng biến trên mỗi khoảng (-∞; -2) và (-2; +∞).
C. Hàm số nghịch biến trên khoảng (-∞; 5).
D. Hàm số nghịch biến trên R \ {-2}
-
Câu 39:
Tìm khoảng nghịch biến của hàm số y = 2x3 – 9x2 + 12x + 4
A. (1; 2).
B. (-∞; 1).
C. (2; 3).
D. (2; +∞).
-
Câu 40:
Các khoảng đồng biến của hàm số y = - x3 + 3x2 + 1 là
A. (-∞; 0), (2; +∞).
B. (0; 2).
C. (-2; 2)
D. (-2; 0).
-
Câu 41:
Cho hàm số y = - x4 + 2x2. Hỏi hàm số đã cho đồng biến trên khoảng nào sau đây?
A. (-∞; +∞)
B. (3; +∞)
C. (-∞; -1)
D. (0; 2)
-
Câu 42:
Hàm số y = x3 – 3x2 – 9x + 1 đồng biến trên mỗi khoảng:
A. (-1; 3) và (3; +∞)
B. (-∞; -1) và (1; 3)
C. (-∞; 3) và (3; +∞)
D. (-∞; -1) và (3; +∞)
-
Câu 43:
Cho hàm số \(y = \frac{1}{4}{x^4} - 2{x^2} + 3\). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (-2; 0) và (2; +∞)
B. Hàm số đồng biến trên khoảng (-∞; -2) và (2; +∞)
C. Hàm số nghịch biến trên khoảng (-∞; -2) và (0; 2)
D. Hàm số nghịch biến trên khoảng (-∞; 0).
-
Câu 44:
Cho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\). Tìm mệnh đề đúng
A. Hàm số luôn nghịch biến trên R \ {-1}
B. Hàm số luôn đồng biến trên R \ {-1}
C. Hàm số nghịch biến trên (-∞; -1); (-1; +∞)
D. Hàm số đồng biến trên (-∞; -1) và (-1; +∞)
-
Câu 45:
Hàm số nào sau đây luôn đồng biến trên từng khoảng xác định của chúng?
A. \(y = \frac{2}{x}\)
B. \(y = \frac{{2x + 3}}{{x - 1}}\)
C. \(y = x - \frac{1}{{x - 1}}\)
D. \(y = x + \frac{{10}}{x}\)
-
Câu 46:
Cho hàm số y = x4 – 2x2 + 3. Tìm các khoảng đồng biến của hàm số
A. (-∞; -1) và (0; 1)
B. (-1; 0) và (1; +∞)
C. (-∞; 0) và (1; +∞)
D. R
-
Câu 47:
Hàm số y = x3 – 3x đồng biến trên khoảng nào?
A. (-∞; 0)
B. (-1;1).
C. (0; +∞).
D. (-∞; +∞).
-
Câu 48:
Hàm số \(y = - {x^3} + 3{x^2} + 2\) đồng biến trên khoảng nào?
A. (0; 2).
B. (2; +∞).
C. (-∞; +∞)
D. (-∞; 0)
-
Câu 49:
Hỏi hàm số \(y = - \frac{1}{3}{x^3} + 2{x^2} + 5x - 44\) đồng biến trên khoảng nào?
A. (-∞; -1).
B. (-∞; 5)
C. (5; +∞)
D. (-1; 5).
-
Câu 50:
Hàm số y = x3 – 3x2 + 2 đồng biến trên khoảng nào trong các khoảng cho dưới đây
A. (0; 2)
B. (-∞; 2).
C. (2; +∞).
D. R
