Trắc nghiệm Sự đồng biến, nghịch biến của hàm số Toán Lớp 12
-
Câu 1:
Hàm số y = - x3 + 3x – 5 đồng biến trên khoảng nào sau đây?
A. (-1; 1).
B. (-∞; -1).
C. (1; +∞).
D. (-∞; 1).
-
Câu 2:
Các khoảng nghịch biến của hàm số y=−14x4+2x2−5y=−14x4+2x2−5 là
A. (-2; 0) và (2; +∞).
B. (-1; 0) và (1 ; +∞)
C. (-∞; -2) và (0 ; 2).
D. (-∞; -1) và (1; +∞)
-
Câu 3:
Cho hàm số y = x4 – 2x2 – 3. Khẳng định nào sau đây là sai?
A. Hàm số nghịch biến trên khoảng (-∞; -1)
B. Hàm số nghịch biến trên khoảng (0; 1)
C. Hàm số nghịch biến trên khoảng (-1; 0)
D. Hàm số đồng biến trên khoảng (1; +∞)
-
Câu 4:
Cho hàm số y=13x3−12x2−12x−1y=13x3−12x2−12x−1. Mệnh đề nào sau đây đúng ?
A. Hàm số đồng biến trên khoảng (4; +∞)
B. Hàm số nghịch biến trên khoảng (-3; +∞)
C. Hàm số đồng biến trên khoảng (-∞; 4)
D. Hàm số đồng biến trên khoảng (-3; 4)
-
Câu 5:
Cho hàm số y=3−xx+1y=3−xx+1. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên mỗi khoảng (-∞; -1) và (-1; +∞)
B. Hàm số nghịch biến với mọi x ≠ 1
C. Hàm số nghịch biến trên tập R \ {-1}
D. Hàm số nghịch biến trên mỗi khoảng (-∞; -1) và (-1; +∞)
-
Câu 6:
Cho hàm số y = x4 – 8x2 – 4. Các khoảng đồng biến của hàm số là:
A. (-2;0) và (2; +∞)
B. (-2; 0) và (0; 2)
C. (-∞; -2) và (0; 2).
D. (-∞; -2) và (2; +∞)
-
Câu 7:
Hàm số y = x3 – 3x2 nghịch biến trên khoảng nào dưới đây?
A. (-1;1).
B. (-∞; 1).
C. (0; 2).
D. (2; +∞).
-
Câu 8:
Hàm số y = x4 – 2x2 – 1 đồng biến trên khoảng nào sau đây:
A. (-∞; -1) và (0; 1)
B. (-1; 0) và (0; 1)
C. (-1;0) và (1; +∞)
D. Đồng biến trên R
-
Câu 9:
Hỏi hàm số y = 2x3 + 3x2 + 5 nghịch biến trên khoảng nào?
A. (-∞; -1)
B. (-1; 0)
C. (0; +∞)
D. (-3; 1)
-
Câu 10:
Các khoảng đồng biến của hàm số y = x3 – 3x2 + 2 là :
A. (-∞; 0).
B. (0; 2).
C. (-∞; 0)∪(2; +∞).
D. (-∞; 0) và (2; +∞)
-
Câu 11:
Cho hàm số y = - x3 – x2 + 5x + 4. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên (−53;1)(−53;1)
B. Hàm số đồng biến trên (−53;1)(−53;1)
C. Hàm số đồng biến trên (−∞;−53)(−∞;−53)
D. Hàm số đồng biến trên (1;+∞)(1;+∞)
-
Câu 12:
Hàm số y = x4 – 2x2 + 3 đồng biến trên các khoảng nào?
A. R
B. (-1 ; 0) và (0 ; 1).
C. (-∞; -1) và (0 ; 1).
D. (-1 ;0) và (1; +∞)
-
Câu 13:
Hàm số y=x2+3x+1y=x2+3x+1 nghịch biến trên khoảng nào?
A. (-3;1).
B. (1; +∞).
C. (-∞; -3).
D. (-3; -1) và (-1; 1)
-
Câu 14:
Cho hàm số y = - x3 + 6x2 – 4. Mệnh đề nào dưới đây sai?
A. Hàm số đạt cực trị tại x = 0
B. Hàm số nghịch biến trên khoảng (-∞;1)
C. Hàm số đồng biến trên khoảng (0;4)
D. Đồ thị hàm số không có tiệm cận
-
Câu 15:
Cho hàm số y = - x3 + 3x2 – 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số đạt cực đại tại x = 1
B. Hàm số luôn luôn nghịch biến
C. Hàm số luôn luôn đồng biến
D. Hàm số đạt cực tiểu tại x = 1
-
Câu 16:
Khẳng định nào sau đây là khẳng định sai về hàm số y=2x−1x+1y=2x−1x+1
A. Hàm số đồng biến trên (1; +∞)
B. Hàm số đồng biến trên R \ {-1}
C. Hàm số có cực trị
D. Hàm số đồng biến trên (-∞;-1)
-
Câu 17:
Tìm tất cả giá trị của m để hàm số y=(m+1)x−2x−my=(m+1)x−2x−m đồng biến trên từng khoảng xác định
A. −2≤m≤1−2≤m≤1
B. [m>1m<−2[m>1m<−2
C. - 2 < m < 1
D. [m>1m≤−2[m>1m≤−2
-
Câu 18:
Với giá trị nào của m thì hàm số y=mx+4x+my=mx+4x+m đồng biến trên khoảng (1;+∞)
A. - 2 < m < 2
B. [m>2m<−2[m>2m<−2
C. m > 2
D. m < - 2
-
Câu 19:
Tìm tất cả các giá trị thực của tham số m đề hàm số nghịch biến trên khoảng (1;+∞)
A. 0 < m ≤ 1
B. 0 < m < 1
C. m > 1
D. 0 ≤ m < 1
-
Câu 20:
Trong các hàm số sau, hàm số nào nghịch biến trên các khoảng xác định của chúng
A. y=x3+3xy=x3+3x
B. y=x−2x−1y=x−2x−1
C. y=2x−33x−5y=2x−33x−5
D. y=−x4−2x2+3y=−x4−2x2+3
-
Câu 21:
Đâu là hàm số đồng biến trên đoạn [2;5]?
A. y = x
B. y = x(x+1)(x+2)
C. y = x(x+1)(x+2)(x+3)(x+4)
D. Cả A, B và C đều đúng
-
Câu 22:
Cho hàm số y = f(x) = x3 + 3x. Hỏi khẳng định nào sau đây là khẳng định đúng?
A. Hàm số f(x) đồng biến trên R
B. Hàm số f(x) nghịch biến trên (-1;0)
C. Hàm số f(x) nghịch biến trên (-∞;0).
D. Hàm số f(x) không đổi trên R
-
Câu 23:
Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?
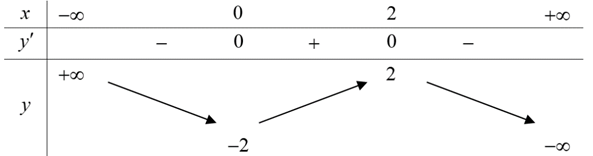
A. y = x3 – 3x2 – 1
B. y = - x3 + 3x2 – 2
C. y = -x3 + 3x2 – 1
D. y = -x3 – 3x – 2
-
Câu 24:
Cho hàm số f(x) = - 2x3 + 3x2 – 3x và 0 ≤ a < b. Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên R
B. f(a) > f(b).
C. f(b) < 0
D. f(a) < f(b).
-
Câu 25:
Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (-1;1)?
A. y=1xy=1x
B. y=x3−3x+1y=x3−3x+1
C. y=1x2y=1x2
D. y=−1xy=−1x
-
Câu 26:
Hàm số nào sau đây đồng biến trên R?
A. y=x√x2+1y=x√x2+1
B. y=tanxy=tanx
C. y=xx+1y=xx+1
D. y=(x2−1)2−3x+2y=(x2−1)2−3x+2
-
Câu 27:
Hàm số nào sau đây nghịch biến trên R?
A. y = -x3 + 3x2 + 3x – 2
B. y = -x3 + 3x2 – 3x – 2.
C. y = x3 + 3x2 + 3x – 2
D. y = x3 – 3x2 – 3x – 2.
-
Câu 28:
Hàm số nào sau đây nghịch biến trên R?
A. y = - x3 + 3x2 + 3x – 2.
B. y = - x3 + 3x2 – 3x – 2
C. y = x3 + 3x2 + 3x – 2
D. y = x3 – 3x2 – 3x – 2
-
Câu 29:
Hàm số nào sau đây đồng biến trên R.
A. y=x−1x+2y=x−1x+2
B. y=x3+4x2+3x−1y=x3+4x2+3x−1
C. y=x4−2x2−1y=x4−2x2−1
D. y=13x3−12x2+3x+1y=13x3−12x2+3x+1
-
Câu 30:
Hàm số nào sau đây nghịch biến trên R.
A. y = - x3 + 2x2 – x – 1
B. y = 1/3 x3 – x2 + 3x + 1
C. y = -1/3.x3 + x2 – x.
D. y = - x3 + 3x + 1
-
Câu 31:
Hàm số nào trong các hàm số sau đây đồng biến trên các khoảng (-∞;2) và (2;+∞)
A. y=2x−5x−2y=2x−5x−2
B. y=x−1x−2y=x−1x−2
C. y=x−1x−6y=x−1x−6
D. y=1x−2y=1x−2
-
Câu 32:
Cho hàm số
f(x)=x2−mx−1f(x)=x2−mx−1 (m khác 1)
Chọn câu trả lời đúng
A. Hàm số luôn giảm trên (-∞;1) và (1;+∞) với m < 1
B. Hàm số luôn giảm trên tập xác định.
C. Hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1
D. Hàm số luôn tăng trên (-∞;1) và (1;+∞)
-
Câu 33:
Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
y=2x+1x+1y=2x+1x+1 (I) ; y = - x4 + x2 – 2 (II); y = x3 – 3x – 5 (III).
A. I và II
B. Chỉ I
C. I và III
D. II và III
-
Câu 34:
Hàm số nào sau đây đồng biến trên tập số thực R?
A. y = x4 – 2x2 – 5
B. y = - x + 1
C. y=x−1x+1y=x−1x+1
D. y = x3 + 3x – 1
-
Câu 35:
Cho hàm số y=f(x) liên tục trên R có f (0)=0 và đồ thị hàm số y=f'(x)như hình vẽ dưới đây
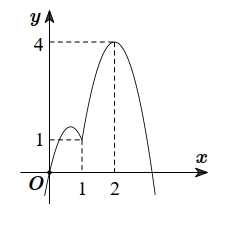
Hàm số y=|3f(x)−x3|3 đồng biến trên khoảng:
A. (2;+∞)
B. (−∞;2)
C. (0;2)
D. (1;3)
-
Câu 36:
Cho hàm số y=f(x) liên tục, nhận giá trị dương trên R và có bảng xét dấu đạo hàm như hình bên.
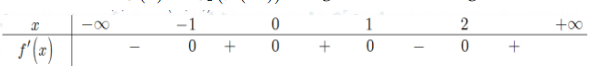
Hàm số g(x)=log2(f(2x)) đồng biến trên khoảng
A. (1;2)
B. (−∞;−1)
C. (−1;0)
D. (−1;1)
-
Câu 37:
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau

Đặt g(x)=f(x−12)−13x3+32x2−2x+3 . Mệnh đề nào dưới đây sai?
A. Hàm số g(x) nghịch biến trên khoảng (-1 ; 0)
B. Hàm số g(x) đồng biến trên khoảng (0;2)
C. Hàm số g(x) nghịch biến trên khoảng (−4;−1)
D. Hàm số g(x) nghịch biến trên khoảng (7;+∞)
-
Câu 38:
Cho hàm đa thức bậc ba y=f(x) có đồ thị hàm số y=f'(x) như hình vẽ. Hàm số g(x)=f(−x−x2) nghịch biến trên khoảng nào dưới đây?
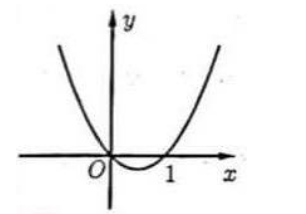
A. (−12;0)
B. (−1;0)
C. (−2;−1)
D. (1;2)
-
Câu 39:
Cho hàm số f (x) có đồ thị của f'(x) như hình vẽ bên. Có bao nhiêu số nguyên m∈[−5;5] để hàm số f(x+m) nghịch biến trên khoảng (1 ; 2) ?
.png)
A. 3
B. 4
C. 5
D. 6
-
Câu 40:
Cho hàm số y=f(x) có đạo hàm trên R . Đồ thị hàm số y=f'(x) như hình vẽ bên dưới.
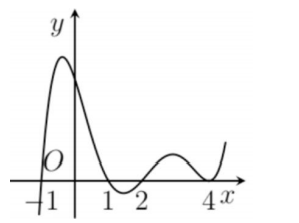
Hàm số g(x)=(12)f(1−2x) nghịch biến trên khoảng nào dưới đây
A. (0;1)
B. (−∞;0)
C. (−1;0)
D. (1;+∞)
-
Câu 41:
Cho hàm số y=f(x) có đạo hàm liên tục trên R . Đồ thị hàm số y=f'(x) như hình vẽ
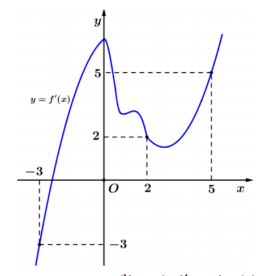
Hàm số g(x)=f(−2x+1)+(x+1)(−2x+4) đồng biến trên khoảng nào dưới đâyA. (−2;−12)
B. (−∞;2)
C. (−12;+∞)
D. (−12;2)
-
Câu 42:
Cho hàm số y =f(x) có bảng xét dấu đạo hàm như hình vẽ

Hàm số y=2f(1−x)+√x2+1−x nghịch biến trên khoảng nào:
A. (−∞;1)
B. (−∞;−2)
C. (−3;−2)
D. (−2;0)
-
Câu 43:
Cho hàm số f(x) có đồ thị y=f'(x) như hình vẽ bên. Hàm số y=f(cosx)+x2−xđồng biến trên khoảng:
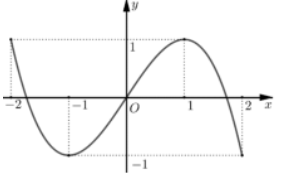
A. (1 ; 2)
B. (-1 ; 0)
C. (0,1)
D. (-2 ;-1)
-
Câu 44:
Cho hàm số f(x)có bảng xét dấu đạo hàm như sau
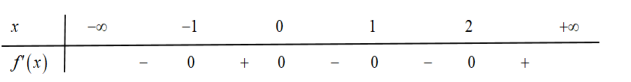
Hàm số y=6f(x−1)−2x3+3x2 đồng biến trên khoảng nào dưới đây?
A. (2;+∞)
B. (−1;0)
C. (−∞;−1)
D. (0;1)
-
Câu 45:
Cho hàm số f(x)có bảng xét dấu đạo hàm như sau:

Hàm số y=f(2x−2)−2ex nghịch biến trên khoảng nào dưới đây?A. (−∞;−1)
B. (−2;0)
C. (0;1)
D. (1;+∞)
-
Câu 46:
Cho hàm số f(x) có đạo hàm liên tục trên R và có đồ thị như hình vẽ bên dưới.
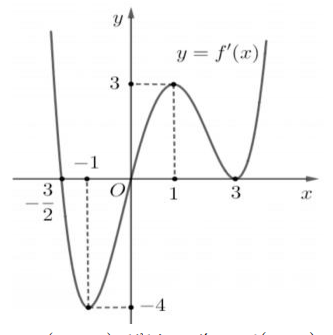
Có bao nhiêu số nguyên m∈(−10;10) để hàm số y=f(3x−1)+x3−3mx đồng biến trên khoảng (-2;1) .
A. 8
B. 6
C. 10
D. 13
-
Câu 47:
Cho hàm số f(x) có bảng xét dấu đạo hàm như sau
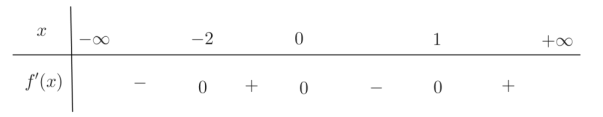
Xét hàm số g(x)=f(1−x)+313x3−32x2+2x . Khẳng định nào sau đây đúng?
A. Hàm số g(x) đồng biến trên khoảng (12;32) .
B. Hàm số g(x) đồng biến trên khoảng (0;2)
C. Hàm số g(x) đồng biến trên khoảng (3;+∞)
D. Hàm số g(x) nghịch biến trên khoảng (0;1)
-
Câu 48:
Cho hàm số f x có bảng biến thiên như sau
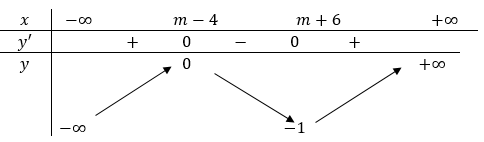
Hàm số y=(f(x))3−3(f(x))2 nghịch biến trên khoảng nào dưới đây?
A. (2;3)
B. (1;2)
C. (3;4)
D. (−∞;−1)
-
Câu 49:
Cho hàm số f(x) có bảng xét dấu đạo hàm f'(x) như sau:
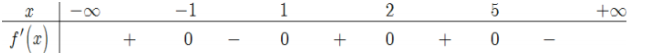
Hàm số y=3f(−x+2)+ex3+3x2−9x+1 nghịch biến trên khoảng nào dưới đây?
A. (−2;1)
B. (2;+∞)
C. (0;2)
D. (−∞;−2)
-
Câu 50:
Cho hàm số y=f(x). Hàm số y=f'(x) có bảng xét dấu:
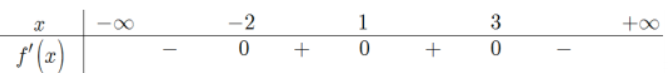
Hàm số y=f(x2+2x) nghịch biến trên khoảng nào dưới đâyA. (-4 ;-3)
B. (0 ; 1)
C. (-2 ;-1)
D. (-2 ; 1)














