Trắc nghiệm Sự đồng biến, nghịch biến của hàm số Toán Lớp 12
-
Câu 1:
Cho hàm số y =f(x) có đồ thị của hàm số\(y=f^{\prime}(x) \) như hình vẽ bên. Hàm số \(y=f\left(3-x^{2}\right)\) đồng biến trên khoảng
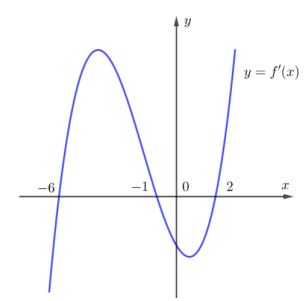
A. (2 ; 3)
B. (-2 ;-1)
C. (0 ; 1)
D. (-1 ; 0)
-
Câu 2:
Cho hàm số y=f(x) có đồ thị f '(x) như hình vẽ
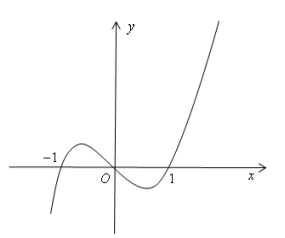
Hàm số \(f\left(x^{2}\right)\) đồng biến khoảng nào dưới đây?
A. \((-\infty ;-1)\)
B. \((-1 ; 0)\)
C. \((0 ; 1)\)
D. \((-1 ;+\infty)\)
-
Câu 3:
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x x^{2}(x-1)\left(x^{2}+m x+5\right)\). Có bao nhiêu số nguyên âm m để hàm số \(y=f\left(x^{2}\right)\)đồng biến trên khoảng \((1 ;+\infty)\)
A. 4
B. 5
C. 6
D. 7
-
Câu 4:
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x(x-1)^{2}\left(x^{2}+m x+9\right)\). Có bao nhiêu giá trị nguyên âm m để hàm số \(y=f(3-x)\) đồng biến trên khoảng \((0 ;+\infty)\).
A. 3
B. 5
C. 4
D. 6
-
Câu 5:
Cho hàm số y=f(x)có đạo hàm \(f^{\prime}(x)=x(x-1)^{2}\left(3 x^{4}+m x^{3}+1\right)\). Có bao nhiêu số nguyên âm m để hàm số \(y=f\left(x^{2}\right)\)đồng biến trên khoảng \((0 ;+\infty)\)
A. 4
B. 5
C. 7
D. 3
-
Câu 6:
Cho hàm số y=f(x) có đạo hàm\(f^{\prime}(x)=x\left(x^{2}-1\right)(x-4)\) . Hàm số y=f(3-x) đồng biến trên khoảng nào dưới đây?
A. \((2 ; 3)\)
B. \((-1 ; 3)\)
C. \((4 ;+\infty) .\)
D. \((3 ; 4)\)
-
Câu 7:
Cho hàm số y =f(x) có đồ thị f'(x) như hình vẽ bên
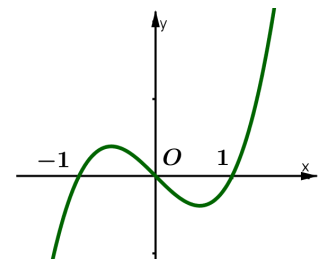
Hàm số \(y=f\left(x^{3}\right)\) đồng biến trên khoảng nào dưới đây?A. \((-\infty ;-1)\)
B. \((1 ;+\infty)\)
C. \((-1 ; 1)\)
D. \((0 ; 1)\)
-
Câu 8:
Cho hàm số y =f(x) có đạo hàm \(f^{\prime}(x)=x^{2}(x-1)(x-4) g(x)\), trong đó \(g(x)>0, \forall x\) .Hàm số \(y=f\left(x^{2}\right)\) đồng biến trên khoảng nào dưới đây?
A. \((-\infty ;-2)\)
B. \((-1 ; 1)\)
C. \((-2 ;-1)\)
D. \((1 ; 2)\)
-
Câu 9:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây
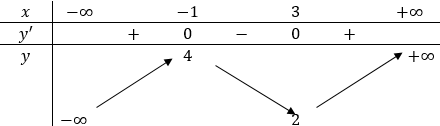
Hàm số y=f(3-x) đồng biến trên khoảng nào dưới đây?
A. \((-\infty ; 0)\)
B. (4;6)
C. (-1;5)
D. (0;4)
-
Câu 10:
Cho hàm số y=f(x) có đạo hàm trên \(\mathbb{R}\) và có đồ thị hàm số y=f'(x) như hình vẽ.
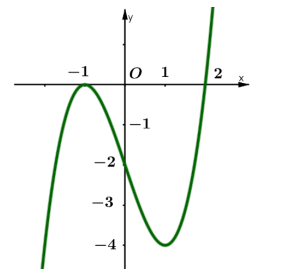
Đặt \(g(x)=f\left(x^{2}-2\right)\) Mệnh đề nào dưới đây sai?
A. Hàm số g(x) đồng biến trên khoảng \((2 ;+\infty)\)
B. Hàm số g(x) nghịch biến trên khoảng (0;2).
C. Hàm số g(x) nghịch biến trên khoảng (-1;0).
D. Hàm số g(x) nghịch biến trên khoảng \((-\infty ;-2)\).
-
Câu 11:
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x(x-1)^{2}(x-2)\). Hỏi hàm số \(y=f\left(\frac{5 x}{x^{2}+4}\right)\) đồng biến trên khoảng nào dưới đây?
A. \((-\infty ;-2)\)
B. \((0 ; 2)\)
C. \((2 ; 4)\)
D. \((-2 ; 1)\)
-
Câu 12:
Cho hàm số y=f(x) có bảng biến thiên như sau
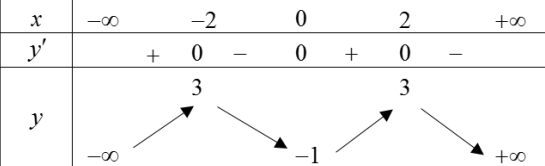
Hàm số \(y=f\left(x^{2}-2\right)\) nghịch biến trên khoảng nào dưới đâyA. \((-2 ; 0)\)
B. \((2 ;+\infty)\)
C. \((0 ; 2)\)
D. \((-\infty ; 0)\)
-
Câu 13:
Cho hàm số y=(x) có đạo hàm \(f'(x)=x^{2}(x-1)\left(x^{2}-4\right)\). Hàm số \(y=f(2-x)\) đồng biến trên khoảng
A. \((-\infty ; 0)\)
B. \((0 ; 1)\)
C. \((2 ;+\infty)\)
D. \((1 ; 4)\)
-
Câu 14:
Cho hàm số \(y=f(x)\). Hàm số\(y=f'(x)\) có đồ thị như hình vẽ bên. Hàm số \(y=f\left(x^{2}-2\right)\) đồng biến trên khoảng
.png)
A. \((0 ; \sqrt{6})\)
B. \((0 ; 1)\)
C. \((-\sqrt{3} ; 0)\)
D. \((1 ; \sqrt{3})\)
-
Câu 15:
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình vẽ bên. Hàm số \(y=f(2-x)\) đồng biến trên khoảng
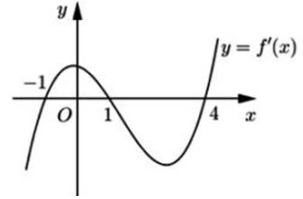
A. \((1 ; 3)\)
B. \((2 ;+\infty)\)
C. \((-2 ; 1)\)
D. \((-\infty ;-2)\)
-
Câu 16:
Cho hàm số \(y=f(x)\). Đồ thị hàm số\(y=f^{\prime}(x)\) như hình vẽ bên. Hàm số \(g(x)=2 f(x)+(x+1)^{2}\) đồng biến trên khoảng nào?
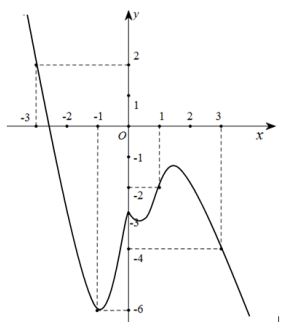
A. \((-3 ; 1)\)
B. \((1 ; 3)\)
C. \((-\infty ; 3)\)
D. \((3 ;+\infty)\)
-
Câu 17:
Cho hàm số y =f(x) có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaceaa9qGaamiEaiabgkziUkabgUcaRiab % g6HiLcqabaGccaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaey % ypa0JaaGymaaaa!43B9! \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 1\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaceaa9qGaamiEaiabgkziUkabgkHiTiab % g6HiLcqabaGccaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaey % ypa0JaeyOeI0IaaGymaaaa!44B1! \mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 1\) . Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y =1 và y = -1 .
B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x =1 và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgUcaRiaaigdaaeaacaaI0aWaaWbaaSqa % beaacaWG4baaaaaaaaa!3C89! y = \frac{{x + 1}}{{{4^x}}}\) .
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho không có tiệm cận ngang.
-
Câu 18:
Tìm tất cả giá trị thực của tham số m để hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqcLbAacaWG5b % Gaeyypa0JcdaWcaaqaaKqzGgGaaGymaaGcbaqcLbAacaaIZaaaaiaa % dIhakmaaCaaaleqabaGaaG4maaaajugObiabgkHiTiaaikdacaWGTb % GaamiEaOWaaWbaaSqabeaacaaIYaaaaKqzGgGaey4kaSIaaiikaiaa % d2gacqGHRaWkcaaIZaGaaiykaiaadIhacqGHRaWkcaWGTbGaeyOeI0 % IaaGynaaaa!4EA4! y = \frac{1}{3}{x^3} - 2m{x^2} + (m + 3)x + m - 5\) đồng biến trên R
A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqcLbAacqGHsi % slkmaalaaabaqcLbAacaaIZaaakeaajugObiaaisdaaaGaeyizImQa % amyBaiabgsMiJkaaigdaaaa!40C4! - \frac{3}{4} \le m \le 1\)
B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqcLbAacaWGTb % GaeyyzImRaaGymaaaa!3A76! m \ge 1\)
C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqcLbAacqGHsi % slkmaalaaabaqcLbAacaaIZaaakeaajugObiaaisdaaaGaeyipaWJa % amyBaiabgYda8iaaigdaaaa!3F62! - \frac{3}{4} < m < 1\)
D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqcLbAacaWGTb % GaeyizImQaeyOeI0IcdaWcaaqaaKqzGgGaaG4maaGcbaqcLbAacaaI % 0aaaaaaa!3E54! m \le - \frac{3}{4}\)
-
Câu 19:
Hàm số \(y=\frac{x^{3}}{3}-\frac{m x^{2}}{2}-2 x+1\) đồng biến trên tập xác định khi:
A. \(m<-2 \sqrt{2}\)
B. \(-8 \leq m \leq 1\)
C. \(m>2 \sqrt{2}\)
D. Không có giá trị m
-
Câu 20:
Giá trị nhỏ nhất của m để hàm số \(y=\frac{1}{3} x^{3}+m x^{2}-m x-m\) đồng biến trên \(\mathbb{R}\) là?
A. -1
B. 0
C. 1
D. 2
-
Câu 21:
Với giá trị nào của m hàm số \(y=\frac{m x+4}{x+m}\) nghịch biến trên từng khoảng xác định của nó:
A. \(\left[\begin{array}{l}m>2 \\ m<-2\end{array}\right.\)
B. \(-2<m<2\)
C. \(-2 \leq m \leq 2\)
D. \(\left[\begin{array}{l}m \geq 2 \\ m \leq-2\end{array}\right.\)
-
Câu 22:
Tìm m để hàm số y\(y=x^{3}-3 m^{2} x\) đồng biến trên các khoảng xác định của nó
A. \(m \geq 0\)
B. \(m \leq 0\)
C. \(m<0\)
D. \(m=0\)
-
Câu 23:
Tìm m để hàm số \(y=\frac{x-m}{x+1}\) đồng biến trên từng khoảng xác định của chúng.
A. \(m \geq-1\)
B. \(m>-1\)
C. \(m \geq 1\)
D. \(m>1\)
-
Câu 24:
Tìm tham số m để hàm số \(y=\frac{1}{3}(m-1) x^{3}+m x^{2}+(3 m-2) x\) là hàm đồng biến trên tập xác định của nó?
A. \(m \geq 2\)
B. \(m<0\)
C. \(m<1\)
D. \(m=\varnothing\)
-
Câu 25:
Với giá trị nào của tham số m thì hàm số nghịch \(y=\frac{m x+3}{3 x+m}\) biến trên từng khoảng xác định của nó?
A. \(-3<m \leq 3\)
B. \(-3 \leq m<3\)
C. \(-3 \leq m \leq 3\)
D. \(-3<m<3\)
-
Câu 26:
Hàm số \(y=\frac{1}{3} x^{3}+(m+1) x^{2}-(m+1) x+1\) đồng biến trên tập xác định của nó khi?
A. \(-2<m \leq-1\)
B. \(-2 \leq m \leq-1\)
C. \(-2 \leq m<-1\)
D. \(-2<m<-1\)
-
Câu 27:
Tìm tham số m thì hàm số \(y=\frac{1}{3} x^{3}-m x^{2}+(2 m-1) x-m+2\) đồng biến trên R?
A. m=2
B. m>1
C. m=1
D. m<1
-
Câu 28:
Tìm tham số m để hàm số \(f(x)=-\frac{x^{3}}{3}+(m-1) x^{2}+(m+3) x\) đồng biến trên khoảng (0;3)
A. \(m \geq \frac{12}{7}\)
B. \(m>\frac{12}{7}\)
C. \(m \leq \frac{12}{7}\)
D. \(m=\frac{12}{7}\)
-
Câu 29:
Hàm số \(y=x^{2}+2(m-2) x+1\) đồng biến trên khoảng \((1;+\infty)\) khi:
A. \(m \geq 1\)
B. \(m<1\)
C. \(m \geq 0\)
D. \(m<0\)
-
Câu 30:
Với giá trị nào của m thì hàm số \(y=x^{3}-6 x^{2}+m x+1\) đồng biến trên khoảng \((0;+\infty)\)
A. \(m<0\)
B. \(m>12\)
C. \(m \leq 0\)
D. \(m \geq 12\)
-
Câu 31:
Hàm số \(y=\frac{x+2}{x-m}\) đồng biến trên khoảng \((2;+\infty)\) khi
A. \(m<2\)
B. \(m>2\)
C. \(m<2\)
D. \(m<-2\)
-
Câu 32:
Tìm m để hàm số:\(y=2 x^{3}-3(2 m+1) x^{2}+6 m (m+1 )x+1\) đồng biến trên khoảng \((2 ;+\infty)\)
A. \(m \leq 1\)
B. \(m \leq 2\)
C. \(\mathrm{m} \leq-1\)
D. \(m>-1\)
-
Câu 33:
Tìm m để hàm số \(y=-x^{3}+3 x^{2}+3 m x-1\) nghịch biến trên \((0;+\infty)\)
A. \(m \leq 1\)
B. \(m \leq 2\)
C. \(\mathrm{m} \leq-1\)
D. \(m>-1\)
-
Câu 34:
Cho hàm số \(y=x^{3}+3 x^{2}-m x-4\) . Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng \((-\infty ; 0)\)
A. \(m \leq-3\)
B. \(m>3\)
C. \( \mathrm{m} \geq 3\)
D. \(m<3\)
-
Câu 35:
Cho hàm số \(y=\frac{mx+2m–3}{x–m}\) (m là tham số). Tìm tất cả các giá trị của m sao cho hàm số nghịch biến trên khoảng \((2;+\infty)\)
A. \(\left[\begin{array}{l} 1<m < 2 \\ m<-3 \end{array}\right.\)
B. \(\left[\begin{array}{l} 1<m \leq 2 \\ m>-3 \end{array}\right.\)
C. Không tồn tại m
D. \(\left[\begin{array}{l} 1<m \leq 2 \\ m<-3 \end{array}\right.\)
-
Câu 36:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{x+2–2m}{x+m}\) đồng biến trên (–1;2).
A. \(m \geq 1\)
B. \(m>2\)
C. \(m<-3\)
D. \(m \le - 1\)
-
Câu 37:
Tìm m để hàm số \(y=\frac{(m+1) x-1}{2 m x+1}\) đồng biến trên khoảng (0;1).
A. \(m>-\frac{1}{3}\)
B. \(m\le-\frac{1}{3}\)
C. \(m<-\frac{1}{3}\)
D. \(m\ge-\frac{1}{3}\)
-
Câu 38:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{x}{x-m}\) đồng biến trên khoảng \((1 ;+\infty)\)
A. \(m>0\)
B. \(0<m < 1\)
C. \(0<m \leq 1\)
D. \(m \leq 1\)
-
Câu 39:
Cho hàm số \(y=x^3-(m+1)x^2-(m^2-2m)x+2020\). Tìm m để hàm số nghịch biến trên khoảng (0;1)
A. \(1 < m < \frac{3}{2}\)
B. \(1 \leq m \leq \frac{3}{2}\)
C. \(-\frac{3}{2} \leq m \leq -1\)
D. \(-1 \leq m \leq \frac{3}{2}\)
-
Câu 40:
Cho hàm số \(y=\frac{3 x-2}{m x+1}\). Tìm m để hàm số đã cho đồng biến trên từng khoảng xác định.
A. \(m>-\frac{3}{2}\)
B. \(m<-\frac{3}{2}\)
C. \(m\ge -\frac{3}{2}\)
D. \(m\le-\frac{3}{2}\)
-
Câu 41:
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaaeaaaaaaaaa8 % qacaWG5bGaeyypa0JaeyOeI0IaamiEa8aadaahaaWcbeqaa8qacaaI % 0aaaaOGaey4kaSIaaGioaiaadIhapaWaaWbaaSqabeaapeGaaGOmaa % aakiabgUcaRiaaiAdaaaa!3FD9! y = - {x^4} + 8{x^2} + 6\) đồng biến trên khoảng nào dưới đây?
A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaaeaaaaaaaaa8 % qadaqadaqaaiabgkHiTiabg6HiLkaacUdacqGHsislcaaIYaaacaGL % OaGaayzkaaaaaa!3BD1! \left( { - \infty ; - 2} \right)\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaaeaaaaaaaaa8 % qadaqadaqaaiaaikdacaGG7aGaey4kaSIaeyOhIukacaGLOaGaayzk % aaaaaa!3AD9! \left( {2; + \infty } \right)\)
B. (-2;2)
C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaaeaaaaaaaaa8 % qadaqadaqaaiabgkHiTiabg6HiLkaacUdacqGHsislcaaIYaaacaGL % OaGaayzkaaaaaa!3BD1! \left( { - \infty ; - 2} \right)\) và (0;2)
D. (-2;0) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaaeaaaaaaaaa8 % qadaqadaqaaiaaikdacaGG7aGaey4kaSIaeyOhIukacaGLOaGaayzk % aaaaaa!3AD9! \left( {2; + \infty } \right)\)
-
Câu 42:
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaWG4bWaaWba % aSqabeaacaaIYaaaaOGaeyOeI0IaamiEaiabgUcaRiaaiodaaaa!404F! y = {x^3} - {x^2} - x + 3\) nghịch biến trên khoảng
A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % GHsislcqGHEisPcaGG7aGaaGPaVlabgkHiTmaalaaabaGaaGymaaqa % aiaaiodaaaaacaGLOaGaayzkaaaaaa!3E9A! \left( { - \infty ;\, - \frac{1}{3}} \right)\)
B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIXaGaai4oaiaaykW7cqGHRaWkcqGHEisPaiaawIcacaGLPaaaaaa!3CD5! \left( {1;\, + \infty } \right)\)
C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % GHsisldaWcaaqaaiaaigdaaeaacaaIZaaaaiaacUdacaaMc8UaaGym % aaGaayjkaiaawMcaaaaa!3CF7! \left( { - \frac{1}{3};\,1} \right)\)
D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % GHsislcqGHEisPcaGG7aGaaGPaVlabgkHiTmaalaaabaGaaGymaaqa % aiaaiodaaaaacaGLOaGaayzkaaaaaa!3E9A! \left( { - \infty ;\, - \frac{1}{3}} \right)\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIXaGaai4oaiaaykW7cqGHRaWkcqGHEisPaiaawIcacaGLPaaaaaa!3CD5! \left( {1;\, + \infty } \right)\)
-
Câu 43:
Hàm số nào sau đây luôn nghịch biến trên R
A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iGacYgacaGGVbGaai4zamaaBaaaleaadaWcaaqaaiaaigdaaeaa % caaIZaaaaaqabaGccaWG4baaaa!3D83! y = {\log _{\frac{1}{3}}}x\)
B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaadIhadaahaaWcbeqaaiaaisdaaaGccqGHRaWkcaaI % 0aGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaisdaaaa!4012! y = - {x^4} + 4{x^2} - 4\)
C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaaI % YaGaamiEaiabgUcaRiaaiodaaaa!3F1B! y = - {x^3} - 2x + 3\)
D. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgUcaRiaaikdaaeaacaWG4bGaeyOeI0Ia % aGymaaaaaaa!3D48! y = \frac{{x + 2}}{{x - 1}}\)
-
Câu 44:
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpdaWc % aaqaaiabgkHiTiaaikdaaeaacqGHsislcaWG4bGaey4kaSIaaGymaa % aaaaa!41AF! y = f\left( x \right) = \frac{{ - 2}}{{ - x + 1}}\) có tính chất
A. Đồng biến trên R
B. Nghịch biến trên R
C. Nghich biến trên các khoảng xác định
D. Đồng biến trên từng khoảng xác định
-
Câu 45:
Cho hàm số \(y=x^{3}+2(m+1) x^{2}-3 m x+5-m\) với m là tham số. tìm diều kiện của m đẻ hàm số đồng biến trên tập xác định?
A. \(\frac{-5-\sqrt{21}}{2} < m < \frac{-5+\sqrt{21}}{2}\)
B. \(\frac{-5-\sqrt{21}}{2} \leq m \leq \frac{-5+\sqrt{21}}{2}\)
C. \(-4 < m < \frac{-1}{4}\)
D. \(-4 \le m \le \frac{-1}{4}\)
-
Câu 46:
Cho hàm số \(y=\frac{mx+2–2m}{x+m}\,\,\,\,\,(1)\) (m là tham số). Tìm m để hàm số (1) đồng biến trên từng khoảng xác định.
A. \(\left[\begin{array}{l} m>-1+\sqrt{3} \\ m<-1-\sqrt{3} \end{array}\right.\)
B. \(\left[\begin{array}{l} m\ge-1+\sqrt{3} \\ m\ge-1-\sqrt{3} \end{array}\right.\)
C. \(-1-\sqrt3<m<-1-\sqrt{3}\)
D. \(-1-\sqrt3\le m\le -1-\sqrt{3}\)
-
Câu 47:
Điều kiện cần và đủ để hàm số \(y=\frac{m x+5}{x+1}\) đồng biến trên từng khoảng xác định là?
A. \(m<5\)
B. \(m>5\)
C. \(m\le-5\)
D. \(m\ge-5\)
-
Câu 48:
Trong tất cả các giá trị của tham số m để hàm số \(y=\frac{1}{3}x^3+mx^2–mx–m \) đồng biến trên R, giá trị nhỏ nhất của m là?
A. 2
B. 1
C. -2
D. -1
-
Câu 49:
Tìm tham số m để hàm số \(y=\frac{1}{3}x^3+(m+1)x^2–(m+1)x+1\) đồng biến trên tập xác định.
A. \(-2 \leq m \leq-1\)
B. \(-2 < m <-1\)
C. \(\begin{array}{l} \left[ \begin{array}{l} m \le - 2\\ m \ge - 1 \end{array} \right. \end{array}\)
D. \(\left[ \begin{array}{l} m < - 2\\ m > - 1 \end{array} \right.\)
-
Câu 50:
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaisdaaaGccqGHsislcaaI0aGaamiE % amaaCaaaleqabaGaaG4maaaakiabgUcaRiaaiodaaaa!3F24! y = {x^4} - 4{x^3} + 3\) đồng biến trên những khoảng nảo sau đây?
A. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % GHsisldaGcaaqaaiaaikdaaSqabaGccaGG7aGaaGimaaGaayjkaiaa % wMcaaiaacYcadaqadaqaamaakaaabaGaaGOmaaWcbeaakiaacUdacq % GHRaWkcqGHEisPaiaawIcacaGLPaaaaaa!40F0! \left( { - \sqrt 2 ;0} \right),\left( {\sqrt 2 ; + \infty } \right)\)
B. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % GHsislcqGHEisPcaGG7aGaeyOeI0YaaOaaaeaacaaIYaaaleqaaaGc % caGLOaGaayzkaaGaaiilamaabmaabaGaaGimaiaacUdadaGcaaqaai % aaikdaaSqabaaakiaawIcacaGLPaaaaaa!40FB! \left( { - \infty ; - \sqrt 2 } \right),\left( {0;\sqrt 2 } \right)\)
C. \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIZaGaai4oaiabgUcaRiabg6HiLcGaayjkaiaawMcaaaaa!3B4C! \left( {3; + \infty } \right)\)
D. (0;3)
