Trắc nghiệm Sự đồng biến, nghịch biến của hàm số Toán Lớp 12
-
Câu 1:
Hàm số y=x3−3x2−9x+1 đồng biến trên khoảng nào trong những khoảng sau?
A. (4;5)
B. (0;4)
C. (-2;2)
D. (-1;3)
-
Câu 2:
Định m để hàm số y=mx+1x+mluôn đồng biến trên từng khoảng xác định của nó
A. [m<−1m>1
B. −1<m<1
C. m<-1
D. m>1
-
Câu 3:
: Với giá trị nào của m, hàm số f(x)=mx3−3x2+(m−2)x+3 nghịch biến trên R ?
A. m<1
B. m>−1
C. m≤−1
D. m≥1
-
Câu 4:
Cho hàm số y=f(x) có đạo hàm và liên tục trên tập số thực R. Biết đồ thị hàm số y=f′(x) như hình vẽ bên dưới. Hỏi hàm số y=f(x2) nghịch biến trong khoảng nào sau đây?
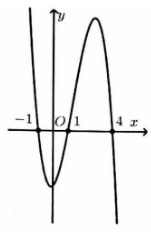
A. (−∞;−2)
B. (-1;0)
C. (1;2)
D. (2;+∞)
-
Câu 5:
Cho hàm số y=f(x) có đạo hàm và liên tục trên tập số thực R. Biết đồ thị hàm số y=f′(x) như hình vẽ bên dưới. Hỏi hàm số y=f(3x–9) đồng biến trong khoảng nào sau đây?
.png)
A. (-2;-1)
B. (83;113)∪(4;+∞)
C. (113:+∞)
D. (-1;2)
-
Câu 6:
Cho hàm số y=f(x) có đạo hàm và liên tục trên tập số thực R. Biết đồ thị hàm số y=f′(x) như hình vẽ bên dưới. Hỏi hàm số y=f(6–2x) nghịch biến trong khoảng nào sau đây?
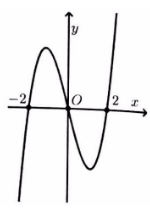
A. (2;+∞)
B. (−∞;2)
C. (0;3)
D. (5;8)
-
Câu 7:
Cho hàm số y=f(x) có đạo hàm và liên tục trên tập số thực R, có đồ thị hàm số y=f′(x) như hình vẽ. Hỏi hàm số y=f(2x–5) đồng biến trong khoảng nào?
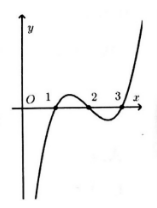
A. (3;72)
B. (1;2)
C. (3;+∞)
D. (−∞;1)
-
Câu 8:
Hàm số y=f(x) có đồ thị hàm số y=f'(x) như hình vẽ. Hỏi đồ thị hàm số y=f(2x2+1) đồng biến trong khoảng nào dưới đây?

A. (−1;+∞)
B. (−∞;0)
C. (-1;1)
D. (0;+∞)
-
Câu 9:
Cho hàm số y=f(x) có đồ thị như hình vẽ. Hỏi hàm số y=f(3x−1) nghịch biến trong khoảng nào?
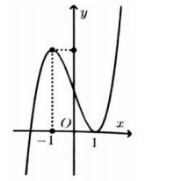
A. (-1;1)
B. (-4;2)
C. (0;23)
D. (13;2)
-
Câu 10:
Cho hàm số y = f(x) xác định, liên tục trên (−∞;1), (1;+∞) và có bảng biến thiên sau.
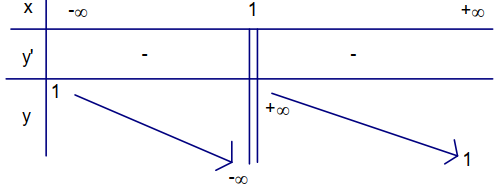
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên (−∞;1) và (1;+∞)
B. Hàm số có giá trị cực tiểu bằng 1
C. Hàm số có giá trị nhỏ nhất bằng 1
D. Hàm số có đúng 1 cực trị
-
Câu 11:
Cho hàm sô y=f(x) có xác định, liên liên tục trên [-2;2] và có đồ thị là đường cong như hình vẽ bên. Khẳng định nào sau đây là đúng?
.png)
A. Hàm số đồng biến trên [-2;2]
B. Hàm số nghịch biến trên (-1;1)
C. Hàm số nghịch biến trên (-2;1)
D. Hàm số đồng biến trên (-1;1)
-
Câu 12:
Cho hàm số y=f(x) có tập xác định là [-3;3] và đồ thị như hình vẽ:
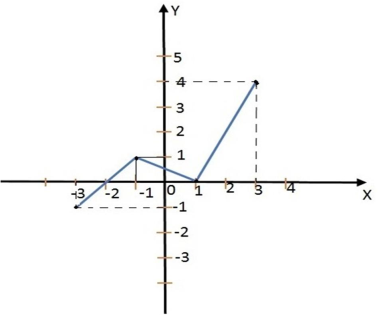
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
B. Hàm số đồng biến trên khoảng (-3;1) và (1;4)
C. Hàm số nghịch biến trên (-2;1)
D. Hàm số đồng biến trên khoảng (-3;-1) và (1;3)
-
Câu 13:
Hàm số nào sau đây có bảng biến thiên như hình dưới?
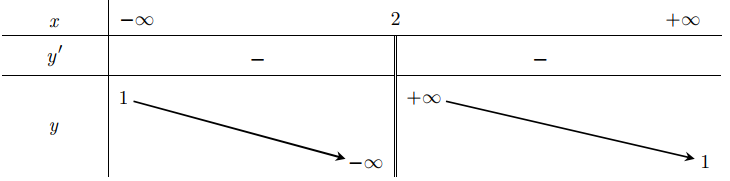
A. y=x+1x−2
B. y=2x−1x+2
C. y=2x+5x+2
D. y=x−3x−2
-
Câu 14:
Hàm số y=x+2x−1nghịch biến trên các khoảng:
A. (−∞;1)∪(1;+∞)
B. (1;+∞)
C. (−1;+∞)
D. (0;+∞)
-
Câu 15:
Các khoảng nghịch biến của hàm số y=2x+1x−1 là:
A. (−∞;1)
B. (1;+∞)
C. (−∞;+∞)
D. (−∞;1)∪(1;+∞)
-
Câu 16:
Hàm số nào sau đây luôn nghịch biến trên từng khoảng xác định D của nó ?
A. y=8−xx+3
B. y=3x−1x+1
C. y=−x+1x−3
D. y=3x+25x+7
-
Câu 17:
Cho hàm số y=x+2x+1 Hãy chọn đáp án đúng ?
A. Hàm số nghịch biến trên (−∞;−1)và(−1;+∞)
B. Hàm số đồng biến trên R∖{−1}
C. Hàm số nghịch biến trên (−∞;−1)∪(−1;+∞)
D. Hàm số nghịch biến với x≠1
-
Câu 18:
Hàm số y=x−1x+1
A. Đồng biến trên R
B. Đồng biến trên R∖{1}
C. Nghịch biến trên R
D. Đồng biến trên (−∞;−1)và(−1;+∞)
-
Câu 19:
Cho hàm số y=14x4−2x2+3. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (−2;0) và (2;+∞)
B. Hàm số đồng biến trên khoảng (−∞;−2)và(2;+∞)
C. Hàm số nghịch biến trên khoảng (−∞;−2)và(0;2)
D. Hàm số nghịch biến trên khoảng (−∞;0)
-
Câu 20:
Hàm số y=x⁴−1 đồng biến trên khoảng nào dưới đây?
A. (−1;+∞)
B. (-1;1)
C. (0;+∞)
D. (−∞;0)
-
Câu 21:
Hàm số y=2(x−3)⁴+1 đồng biến trong khoảng nào sau đây ?
A. (3;+∞)
B. (−∞;3)
C. (−∞;3]
D. [3;+∞)
-
Câu 22:
Hỏi hàm số y=−x⁴+2x²+2 nghịch biến trên khoảng nào trong các khoảng sau đây ?
A. (-3;-2)
B. (-2;-1)
C. (0;1)
D. (1;2)
-
Câu 23:
Hàm số y = -x ⁴ + 4x ² - 2 nghịch biến trên mỗi khoảng nào sau đây ?
A. (−√2;0)và(√2;+∞)
B. (−√2;√2)
C. (√2;+∞)
D. (−∞;−√2)và(0;√2)
-
Câu 24:
Tìm khoảng đồng biến của hàm số y=4x³−x²−4x−2
A. (−12;23)
B. (−∞;−12)
C. (23;+∞)
D. (−∞;−12)và(23;+∞)
-
Câu 25:
Hàm số y = f (x) có bảng biến thiên như sau
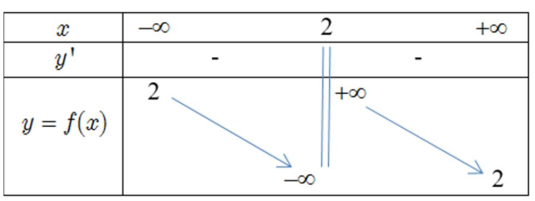
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên R
B. Hàm số nghịch biến trên R∖{−2}
C. Hàm số nghịch biến trên (−∞;2)∪(2;+∞)
D. Hàm số đồng biến trên (−∞;2)∪(2;+∞)
-
Câu 26:
Cho hàm số y = f (x) có đồ thị như hình vẽ. Khi đó f (x ) đồng biến trên các khoảng nào?
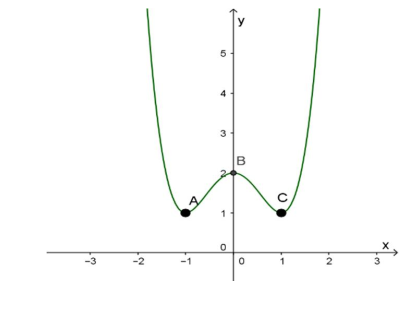
A. (−∞;−1),(1;+∞)
B. (−1;0),(1;+∞)
C. (-1;0),(0;1)
D. (−∞;−1),(−1;0)
-
Câu 27:
Cho hàm số y = f (x ) có bảng biến thiên như hình vẽ bên dưới. Hỏi mệnh đề nào sau đây là sai ?
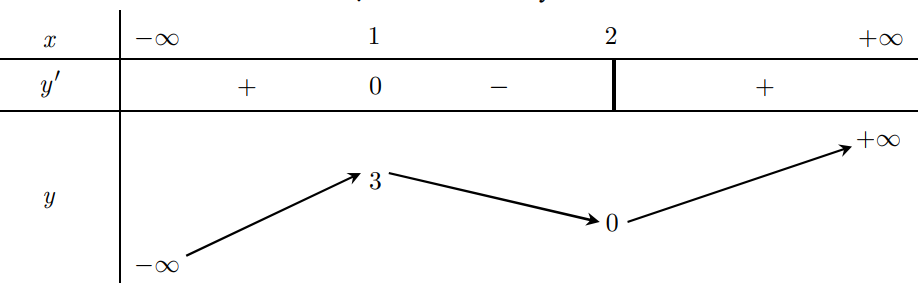
A. Hàm số đã cho đồng biến trên khoảng (2;+∞)
B. Hàm số đã cho đồng biến trên khoảng (3;+∞)
C. Hàm số đã cho đồng biến trên khoảng (−∞;1)
D. Hàm số đã cho nghịch biến trên khoảng (0;3)
-
Câu 28:
Cho hàm số y =f(x) xác định, liên tục trên R và có bảng biến thiên
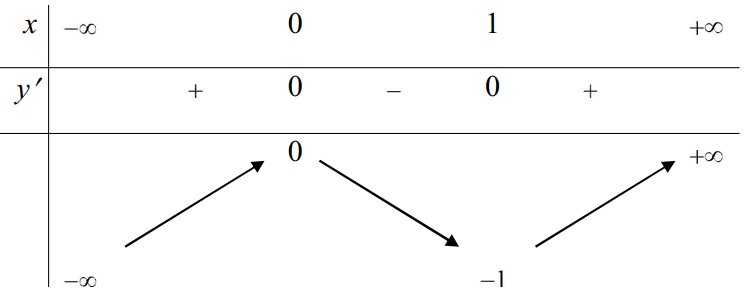
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên R
B. Hàm số nghịch biến trên (−∞;0)
C. Hàm số nghịch biến trên (1;+∞)
D. Hàm số nghịch biến trên (0;1)
-
Câu 29:
Quan sát đồ thị của hàm số y = f (x) dưới đây và chọn mệnh đề đúng:
.png)
A. Hàm số nghịch biến trên (3;+∞)
B. Hàm số đồng biến trên (-1;3)
C. Hàm số nghịch biến trên (−∞;−1)
D. Hàm số đồng biến trên (0;2)
-
Câu 30:
Cho hàm số f ( ) x xác định trên R và có đồ thị hàm số y =f'(x) là đường cong trong hình bên. Hỏi mệnh đề nào dưới đây đúng ?
.png)
A. Hàm số f(x) đồng biến trên (1;2)
B. Hàm số f(x) nghịch biến trên (0;2)
C. Hàm số f(x) đồng biến trên (-2;1)
D. Hàm số f(x) nghịch biến trên (-1;1)
-
Câu 31:
Cho hàm số y=f(x) có bảng biến thiên như hình dưới. Mệnh đề nào sau đây là sai?
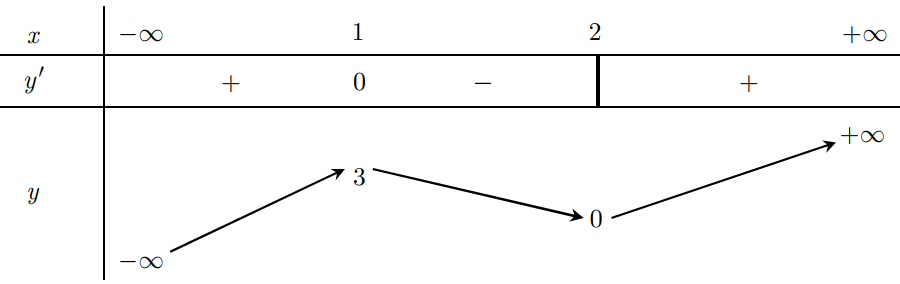
A. Hàm số đã cho đồng biến trên (2;+∞)
B. Hàm số đã cho đồng biến trên (3;+∞)
C. Hàm số đã cho đồng biến trên (−∞;1)
D. Hàm số đã cho nghịch biến trên (0;3)
-
Câu 32:
Hỏi hàm số y=−2x3+3x2+2 đồng biến trên khoảng nào?
A. (−∞;0)
B. (−∞;+∞)
C. (1;+∞)
D. (0;1)
-
Câu 33:
Cho hàm số y=f(x)=2x3+6x2+6x−2017. Mệnh đề nào dưới đây sai
A. Hàm số đã cho đồng biến trên R
B. Hàm số đã cho nghịch biến trên R
C. Trên khoảng (−∞;−2) hàm số đã cho đồng biến
D. Trên khoảng (2;+∞) hàm số đã cho đồng biến
-
Câu 34:
Hàm số y=f(x)=x4−12x3 nghịch biến trên
A. (−∞;0)
B. (0;9)
C. (9;+∞)
D. (−∞;9)
-
Câu 35:
Hàm số y=f(x)=xx−2 nghịch biến trên khoảng nào sau?
A. (−∞;2)
B. (2;+∞)
C. Nghịch biến trên từng khoảng xác định
D. Đáp án khác
-
Câu 36:
Khoảng đồng biến của hàm số y=x4−2x2+1 là
A. (−1;0)∪(1;+∞)
B. (-1;0)
C. (−∞;−1)
D. (0;+∞)
-
Câu 37:
Các khoảng nghịch biến của hàm số y=f(x)=2x3−6x+20 là
A. (−∞;−1)∪(1;+∞)
B. (-1;1)
C. [-1;1]
D. (0;1)
-
Câu 38:
Hàm số y=x+2x−1nghịch biến trên các khoảng:
A. (−∞;1)∪(1;+∞)
B. (1;+∞)
C. (−1;+∞)
D. R
-
Câu 39:
. Hàm số y=f(x)=−x3+3x2−1 đồng biến trên các khoảng:
A. (−∞;1)
B. (0;2)
C. (2;+∞)
D. R
-
Câu 40:
Cho hàm số y=13x3−12x2−12x−1. Mệnh đề nào sau đây đúng ?
A. Hàm số đồng biến trên khoảng (4;+∞)
B. Hàm số nghịch biến trên khoảng (−3;+∞).
C. Hàm số đồng biến trên khoảng (−∞;4)
D. Hàm số đồng biến trên khoảng (-3;4)
-
Câu 41:
Hàm số y=x3−3x2 nghịch biến trên khoảng nào dưới đây
A. (−1;1)
B. (−∞;−1)
C. (0;2)
D. (2;+∞)
-
Câu 42:
Hàm số y=−x3+3x+5 đồng biến trên khoảng nào sau đây
A. (−∞;−1)
B. (−1;1)
C. (−∞;1)
D. (1;+∞)
-
Câu 43:
Cho hàm số y=x3−2x2+x+1. Mệnh đề nào sau đây là đúng
A. Hàm số nghịch biến trên (13;1)
B. Hàm số nghịch biến trên (−∞;13)
C. Hàm số nghịch biến trên (1;+∞)
D. Hàm số đồng biến trên (13;1)
-
Câu 44:
Tập xác định của hàm số f(x)=−x3+3x2−2 là
A. (1;2)
B. (−∞;+∞)
C. [1;2]
D. [-1;2)
-
Câu 45:
Cho hàm số y=xx−1. Chọn khẳng định đúng
A. Hàm số đồng biến trên R∖{1}
B. Hàm số nghịch biến trên R∖{1}
C. Hàm số đồng biến trên (1;+∞)
D. Hàm số nghịch biến trên (1;+∞)
-
Câu 46:
Thể tích khối lăng trụ có diện tích đáy bằng 3a2, chiều cao bằng a là
A. V=a33
B. V=3a3
C. V=a3
D. V=2a33














