Trắc nghiệm Cực trị của hàm số Toán Lớp 12
-
Câu 1:
Nhân ngày phụ nữ Việt Nam 20 -10 - 2021 , ông A quyết định mua tặng vợ một món quà và đặt nó vào trong một chiếc hộp có thể tích là 32 (đvtt) có đáy hình vuông và không có nắp . Để món quà trở nên thật đặc biệt và xứng đáng với giá trị của nó ông quyết định mạ vàng cho chiếc hộp , biết rằng độ dạy lớp mạ tại mọi điểm trên hộp là như nhau . Gọi chiều cao và cạnh đáy của chiếc hộp lần lượt là h; x. Để lượng vàng trên hộp là nhỏ nhất thì giá trị của h; x phải là ?
A. x=4;h=2
B. x=2;h=4
C. x=2;h=2
D. x=4;h=4
-
Câu 2:
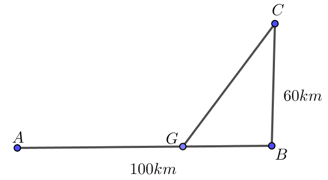
Đường dây điện 110KV kéo từ trạm phát (điểm A) trong đất liền ra Côn Đảo (điểm C). biết khoảng cách ngắn nhất từ C đến B là 60km, khoảng cách từ A đến B là 100km, mỗi km dây điện dưới nước chi phí là 5000 USD, chi phí cho mỗi km dây điện trên bờ là 3000 USD. Hỏi điểm G cách A bao nhiêu để mắc dây điện từ A đến G rồi từ G đến C chi phí ít nhất.
A. 50 (km)
B. 60 (km)
C. 55 (km)
D. 45 (km)
-
Câu 3:
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số \(y=-x^{3}+3 m x+1\) có 2 điểm cực trị A, B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ )
A. \(m=\frac{1}{2}\)
B. \(m=\frac{-3}{2}\)
C. \(m=\frac{5}{2}\)
D. \(m=1\)
-
Câu 4:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=x^{3}-3 m x^{2}+(m-1) x+2\) có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương.
A. \(m\le1\)
B. \(m\ge 1\)
C. \(m>1\)
D. \(m<1\)
-
Câu 5:
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=(m+1) x^{4}-m x^{2}+\frac{3}{2}\) chỉ có cực tiểu mà không có cực đại.
A. \( - 1 \le m \le 0\)
B. \( - 1< m \le 0\)
C. \(m > 0\)
D. \( m \le 0\)
-
Câu 6:
Cho hàm số y = f(x) có đạo hàm trên (a;b). Nếu f'(x) đổi dấu từ âm sang dương qua điểm (x0) thuộc (a;b) thì
A. x0 là điểm cực đại của hàm số
B. x0 là điểm cực tiểu của hàm số
C. x0 là điểm cực đại của đồ thị hàm số.
D. x0 là điểm cực tiểu của đồ thị hàm số
-
Câu 7:
Hàm số \(y = {x^3} – 5{x^2} + 7x – 1\) đạt cực đại tại.
A. x = 1
B. \(x = \frac{7}{3}\)
C. x = – 1
D. \(x = – \frac{7}{3}\)
-
Câu 8:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2}\left( {{x^2} – 1} \right)\). Điểm cực tiểu của hàm số \(y = f\left( x \right)\) là
A. x = 0
B. x = – 1
C. y = 0
D. x = 1
-
Câu 9:
Tìm điểm cực tiểu của hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 3x + 1\)
A. x = – 3
B. x = 1
C. x = 3
D. x = – 1
-
Câu 10:
Cho hàm số \(y = {x^4} – \frac{2}{3}{x^3} – {x^2}.\) Mệnh đề nào sau đây là đúng?
A. Hàm số có hai giá trị cực tiểu là \( – \frac{2}{3}\) và \( – \frac{5}{{48}}\).
B. Hàm số có giá trị cực tiểu là \( – \frac{2}{3}\) và giá trị cực đại là \( – \frac{5}{{48}}\)
C. Hàm số có giá trị cực tiểu là 0
D. Hàm số chỉ có một giá trị cực tiểu.
-
Câu 11:
Hàm số \(y = 2{x^3} – {x^2} + 5\) có điểm cực đại là.
A. \(x = \frac{1}{3}\)
B. x = 5
C. x = 3
D. x = 0
-
Câu 12:
Giá trị cực tiểu của hàm số \(y = {x^3} – 3{x^2} – 9x + 2\) là
A. – 20
B. 7
C. – 25
D. 3
-
Câu 13:
Các điểm cực tiểu của hàm số \(y = {x^4} + 3{x^2} + 2\) là
A. x = 0
B. x = – 1
C. x = 1 và x = 2
D. x = 5
-
Câu 14:
Tìm cực đại của hàm số \(y = – \frac{1}{4}{x^4} + 2{x^2} – 1\)
A. 3
B. 0
C. – 1
D. \(\pm 2\)
-
Câu 15:
Cho hàm số \(y = {x^4} – 4{x^2} + 2\). Khẳng định nào sau đây là ĐÚNG?
A. Hàm số đạt cực tiểu tại điểm y = – 2
B. Hàm số đạt cực tiểu tại điểm x = 0
C. Hàm số đạt cực tiểu tại hai điểm \(x = – \sqrt 2 \) và \(x = \sqrt 2 \)
D. Hàm số đạt cực đại tại hai điểm \(\left( { – \sqrt 2 ; – 2} \right)\) và \(\left( {\sqrt 2 ; – 2} \right)\).
-
Câu 16:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong trong hình vẽ bên. Điểm cực tiểu của đồ thị hàm số \(y = f\left( x \right)\) là
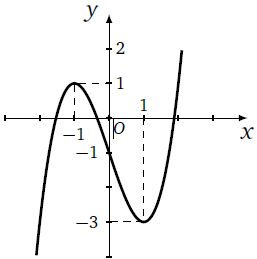
A. x = 1
B. x = – 1
C. \(M\left( { – 1;1} \right)\)
D. \(M\left( {1; – 3} \right)\)
-
Câu 17:
Cho hàm số \(y = \frac{{x + 1}}{{{x^2} + 8}}\). Mệnh đề nào dưới đây là đúng?
A. Điểm cực đại của hàm số x = 2
B. Điểm cực tiểu của hàm số là x = 4
C. Giá trị cực tiểu của hàm số là – 4
D. Giá trị cực đại của hàm số là 2
-
Câu 18:
Hàm số \(y = – {x^4} + 2{x^2} – 3\) có điểm cực đại và điểm cực tiểu \({x_{CT}}\,\) là.
A. \({x_{CT}} = \pm 1\)
B. \({x_{CT}} = 1\)
C. \({x_{CT}} = 0\)
D. \({x_{CT}} = \pm 2\)
-
Câu 19:
Hàm số \(y = 3{x^2} – 2{x^3}\) đạt cực trị tại
A. \({x_{{\rm{CD}}}} = 1;{x_{{\rm{CT}}}} = 0\)
B. \({x_{{\rm{CD}}}} = – 1;{x_{{\rm{CT}}}} = 0\)
C. \({x_{{\rm{CD}}}} = 0;{x_{{\rm{CT}}}} = – 1\)
D. \({x_{{\rm{CD}}}} = 0;{x_{{\rm{CT}}}} = 1\)
-
Câu 20:
Điểm cực đại của đồ thị hàm số \(y = 2{x^3} – 3{x^2} – 2\) là.
A. \(\left( {1; – 3} \right)\)
B. \(\left( {2;2} \right)\)
C. \(\left( {0; – 2} \right)\)
D. \(\left( { – 1; – 7} \right)\)
-
Câu 21:
Tìm điểm cực tiểu của đồ thị \(\left( C \right):y = – {x^3} + 3x + 2\).
A. y = 0
B. \(\left( {1;4} \right)\)
C. \(\left( { – 1;0} \right)\)
D. x = – 1
-
Câu 22:
Tìm điểm cực tiểu của đồ thị hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 3x + 1\).
A. \(\left( {3;1} \right)\)
B. x = 3
C. \(\left( {1;\frac{7}{3}} \right)\)
D. x = 1
-
Câu 23:
Hàm số \(y = {x^4} – {x^2} + 1\) có bao nhiêu điểm cực trị?
A. 2
B. 1
C. 3
D. 0
-
Câu 24:
Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A. \(y = \frac{{2x – 1}}{{x + 1}}\)
B. \(y = {x^4}\)
C. \(y = – {x^3} + x\)
D. \(y = \left| x \right|\)
-
Câu 25:
Hàm số \(y = {x^3} – 5{x^2} + 3x + 1\) đạt cực trị tại:
A. \(\left[ \begin{array}{l}x = – 3\\x = – \frac{1}{3}\end{array} \right.\)
B. \(\left[ \begin{array}{l}x = 0\\x = – \frac{{10}}{3}\end{array} \right.\)
C. \(\left[ \begin{array}{l}x = 3\\x = \frac{1}{3}\end{array} \right.\)
D. \(\left[ \begin{array}{l}x = 0\\x = \frac{{10}}{3}\end{array} \right.\)
-
Câu 26:
Cho hàm số \(y = \frac{{{x^2} + 3x}}{{x – 1}}\). Tọa độ điểm cực đại của đồ thị hàm số là.
A. \(\left( { – 1;1} \right)\)
B. \(\left( {2;10} \right)\)
C. \(\left( {3;9} \right)\)
D. \(\left( { – 3;0} \right)\)
-
Câu 27:
Cho hàm số \(y = \frac{{{x^3}}}{3} – 2{x^2} + 3x + \frac{2}{3}\) có đồ thị là \(\left( C \right)\). Tìm tọa độ điểm cực đại của đồ thị hàm số \(\left( C \right)\).
A. \(\left( {1; – 2} \right)\)
B. \(\left( {3;\frac{2}{3}} \right)\)
C. \(\left( { – 1;2} \right)\)
D. \(\left( {1;2} \right)\)
-
Câu 28:
Điểm cực đại của đồ thị hàm số \(y = {x^3} + 3{x^2} + 2\) là
A. \(\left( {2;0} \right)\)
B. \(\left( {0;2} \right)\)
C. \(( – 2;6)\)
D. \(\left( { – 2; – 18} \right)\)
-
Câu 29:
Cho hàm số \(y = {x^4} + 4{x^2} + 2\). Mệnh đề nào dưới đây là mệnh đề đúng?
A. Hàm số đạt cực tiểu tại x = 0
B. Hàm số có cực đại và không có cực tiểu.
C. Hàm số có cực đại và cực tiểu.
D. Hàm số không có cực trị.
-
Câu 30:
Điểm cực đại của đồ thị hàm số \(y = {x^3} – 3x\) là?
A. \(\left( {1;0} \right)\)
B. \(\left( { – 1;0} \right)\)
C. \(\left( {1; – 2} \right)\)
D. \(\left( { – 1;2} \right)\)
-
Câu 31:
Điểm cực tiểu của đồ thị hàm số \(y = {x^3} – 3x + 5\) là điểm?
A. \(Q\left( {3;{\rm{ }}1} \right)\)
B. \(M\left( {1;{\rm{ }}3} \right)\)
C. \(P\left( {7; – 1} \right)\)
D. \(N\left( { – 1;{\rm{ }}7} \right)\)
-
Câu 32:
Tìm số điểm cực trị của hàm số \(y = {x^4} + 3{x^2} – 3\)?
A. 4
B. 2
C. 3
D. 1
-
Câu 33:
Tìm điểm cực tiểu của đồ thị hàm số \(y = {x^3} + 3{x^2} – 24x – 26\).
A. ( – 2;26)
B. (4; – 10)
C. (2; – 54)
D. ( – 4;54)
-
Câu 34:
Hàm số \(y = \frac{1}{3}{x^3} + 2{x^2} + 3x – 1\) có các điểm cực trị là
A. \(\left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)
B. \(\left[ \begin{array}{l}x = – 1\\x = 3\end{array} \right.\)
C. \(\left[ \begin{array}{l}x = – 1\\x = – 3\end{array} \right.\)
D. \(Hàm số không có cực trị.\)
-
Câu 35:
Hàm số \(y = {x^3} – 3{x^2} + 2\) đạt cực trị tại các điểm:
A. \(x = \pm 1\)
B. \(x = 0,x = 2\)
C. \(x = \pm 2\)
D. \(x = 0,x = 1\)
-
Câu 36:
Tọa độ điểm cực đại của đồ thị hàm số \(y = – 2{x^3} + 3{x^2} + 1\) là:
A. \(\left( { – 1;\,6} \right)\)
B. \(\left( {2;\,3} \right)\)
C. \(\left( {0;\,1} \right)\)
D. \(\left( {1;\,2} \right)\)
-
Câu 37:
Giá trị cực đại của hàm số \(y = {x^3} + 2{x^2} + x + 3\) bằng
A. – 1
B. \(– \frac{1}{3}\)
C. 3
D. \(\frac{{77}}{{27}}\)
-
Câu 38:
Hàm số \(y = {x^3} – 3x\) đạt cực tiểu tại x bằng?
A. – 2
B. – 1
C. 1
D. 0
-
Câu 39:
Điểm cực đại của hàm số \(y = {x^3} – 3{x^2} + 2\) là
A. x = 0
B. x = 2
C. y = – 2
D. y = 2
-
Câu 40:
Cho hàm số \(y = – \frac{2}{3}{x^3} + {x^2} + 1\). Mệnh đề nào sau đây đúng?
A. Điểm cực tiểu của đồ thị hàm số là \(B\left( {0;\;1} \right)\)
B. Điểm cực tiểu của hàm số là \(B\left( {1;\;\frac{4}{3}} \right)\)
C. Điểm cực đại của đồ thị hàm số là \(B\left( {0;\;1} \right)\)
D. Điểm cực đại của hàm số là \(B\left( {1;\;\frac{4}{3}} \right)\)
-
Câu 41:
Điểm cực tiểu của hàm số \(y = – {x^4} + 5{x^2} – 2\) là
A. y = 0
B. x = – 2
C. x = 0
D. y = – 2
-
Câu 42:
Cho hàm số \(y = {x^3} – 3{x^2} + 2\). Khẳng định nào sau đây đúng?
A. Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = – 2.
B. Hàm số đạt cực tiểu tại x = 2 và cực đại tại x = 0.
C. Hàm số đạt cực đại tại x = – 2 và cực tiểu tại x = 0.
D. Hàm số đạt cực đại tại x = 2 và cực tiểu tại x = 0
-
Câu 43:
Tìm tọa độ điểm cực tiểu M của đồ thị hàm số \(y = {x^3} – 3x + 2\).
A. \(M\left( {1;4} \right)\)
B. \(M\left( { – 1;0} \right)\)
C. \(M\left( {1;0} \right)\)
D. \(M\left( { – 1;4} \right)\)
-
Câu 44:
Giá trị cực tiểu \({y_{CT}}\) của hàm số \(y = {x^3} – 3{x^2} + 7\) là
A. \({y_{CT}} = 3\)
B. \({y_{CT}} = 0\)
C. \({y_{CT}} = 2\)
D. \({y_{CT}} = 7\)
-
Câu 45:
Cho hàm số \(y = \frac{{{x^3}}}{3} – 2{x^2} + 3x + \frac{2}{3}\). Tọa độ điểm cực đại của đồ thị hàm số là.
A. \(\left( {1; – 2} \right)\)
B. \(\left( {1;2} \right)\)
C. \(\left( { – 1;2} \right)\)
D. \(\left( {3;\frac{2}{3}} \right)\)
-
Câu 46:
Hàm số \(y = \frac{1}{3}{x^3} – {x^2} + x + 1\) có mấy điểm cực trị?.
A. 0
B. 1
C. 2
D. 3
-
Câu 47:
Đồ thị hàm số nào sau đây có \(3\) điểm cực trị.
A. \(y = – {x^4} – 2{x^2} – 1\)
B. \(y = {x^4} + 2{x^2} – 1\)
C. \(y = 2{x^4} + 4{x^2} + 1\)
D. \(y = {x^4} – 2{x^2} – 1\)
-
Câu 48:
Hàm số \(y = – {x^4} + 8{x^2} – 7\) có bao nhiêu giá trị cực trị?
A. 3
B. `
C. 0
D. 2
-
Câu 49:
Đồ thị hàm số \(y = {x^4} – {x^2} + 1\) có bao nhiêu điểm cực trị?
A. 3
B. 2
C. 1
D. 4
-
Câu 50:
Trong các hàm số sau, hàm số nào có hai điểm cực đại và một điểm cực tiểu?
A. \(y = {x^4} – {x^2} + 3\)
B. \(y = – {x^4} – {x^2} + 3\)
C. \(y = – {x^4} + {x^2} + 3\)
D. \(y = {x^4} + {x^2} + 3\)
