100 câu trắc nghiệm giữa HK1 Toán 11 - Cánh Diều

Câu 1:

Một bình chứa 2 viên bi xanh và 2 viên bi trắng. Chọn ngẫu nhiên hai viên bi. Xác suất để được 1 viên bi xanh và 1 viên bi trắng là:

Lời giải:

Đáp án đúng: D

Ta có \({{n}_{\Omega }}=C_{4}^{2}=6\)

Chọn 1 viên bi xanh có 2 cách.

Chọn 1 viên bi trắng có 2 cách.

Gọi A là biến cố: “Chọn được 1 viên bi xanh và 1 viên bi trắng” \(\Rightarrow {{n}_{A}}=2.2.=4.\)

Vậy xác suất của biến cố A là \(P\left( A \right)=\frac{{{n}_{A}}}{{{n}_{\Omega }}}=\frac{4}{6}=\frac{2}{3}.\)

Chọn D.

Câu 2:

Cho cấp số nhân với \({{u}_{1}}=3;q=-2.\) Số 192 là số hạng thứ mấy của cấp số nhân?

Lời giải:

Đáp án đúng: B

Ta có: \({{u}_{n}}={{u}_{1}}{{q}^{n-1}}.\)

\(\begin{array}{l}192 = {3.(-2)^{x - 1}} \Leftrightarrow {(-2)^{x - 1}} = 64 = {(-2)^6} \Leftrightarrow x = 7.\\ \Rightarrow 192 = {3.(-2)^{7 - 1}} = {u_1}.{q^{7 - 1}} = {u_7}.\end{array}\)

Chọn B.

Câu 3:

Cho phép tịnh tiến theo vector \(\overrightarrow{u}\left( 1;3 \right)\) biến đường thẳng \(d:2x+y+1=0\) thành đường thẳng d’ có phương trình:

Lời giải:

Đáp án đúng: C

Gọi \(d'={{T}_{\overrightarrow{u}}}\left( d \right)\Rightarrow d'\parallel d\Rightarrow \) Phương trình đường thẳng d’ có dạng: \(d':2x+y+c=0.\)

Lấy điểm \(A\left( 0;-1 \right)\in d.\) Gọi \(A'\left( {x,y} \right) = {T_{\overrightarrow u }}\left( A \right) \Leftrightarrow \overrightarrow {AA'} = \overrightarrow u \Leftrightarrow \left( {x - 0;y + 1} \right) = \left( {1;3} \right) \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right. \Rightarrow A'\left( {1;2} \right)\)

Ta có: \(d'={{T}_{\overrightarrow{u}}}\left( d \right);A'={{T}_{\overrightarrow{u}}}\left( A \right)\,\,;\,\,A\in d\Rightarrow A'\in d'\) .

Thay tọa độ điểm A’ vào phương trình đường thẳng d’ ta có: \(2.1+2+c=0\Leftrightarrow c=-4.\)

Vậy phương trình đường thẳng d’: 2x + y – 4 = 0.

Chọn C.

Câu 4:

Cho đường tròn (T) có phương trình \({{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=9.\) Phép vị tự tâm O, tỉ số 2 biến (T) thành đường tròn nào?

Lời giải:

Đáp án đúng: C

Đường tròn (C) có tâm I(1; -2), bán kính R = 3.

Gọi (C’) là ảnh của (C) qua phép vị tự tâm O tỉ số 2.

Gọi R’ là bán kính của đường tròn (C’) qua phép vị tự tâm O tỉ số 2 thì R’=2R=6.

Gọi

\(\begin{array}{l}I'\left( {x;y} \right) = {V_{\left( {O;2} \right)}}\left( I \right) \Leftrightarrow \overrightarrow {OI'} = 2\overrightarrow {OI} \\ \Leftrightarrow \left( {x;y} \right) = 2\left( {1; - 2} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 4\end{array} \right. \Rightarrow I'\left( {2; - 4} \right)\end{array}\)

I là tâm của đường tròn (C) suy ra I’ là tâm của đường tròn (C’).

Vậy (C’) có phương trình: \({{\left( x-2 \right)}^{2}}+{{\left( y+4 \right)}^{2}}=36\)

Chọn C.

Câu 5:

Cho hình chóp S.ABCD. Gọi \(O=AC\cap BD.\) Một mặt phẳng \(\left( \alpha \right)\) cắt SA, SB, SC, SD tại A’, B’, C’, D’. Giả sử \(AB\cap CD=E,A'B'\cap C'D'=E'.\) Tìm phát biểu đúng trong các phát biểu sau:

Lời giải:

Đáp án đúng: A

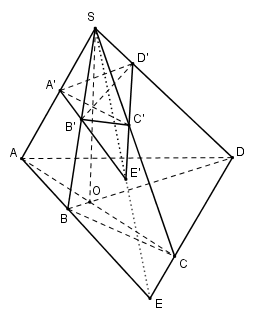
Trong (ABCD) có: \(AB \cap CD = E \Rightarrow \left( {SAB} \right) \cap \left( {SCD} \right) = SE.\)

Ta có: \(\left\{ \begin{array}{l}\left( {A'B'C'D'} \right) \cap \left( {SAB} \right) = A'B'\\\left( {A'B'C'D'} \right) \cap \left( {SCD} \right) = C'D'\\\left( {SAB} \right) \cap \left( {SCD} \right) = SE\end{array} \right. \Rightarrow \) A’B’, C’D’, SE dồng quy. Mà \(A'B' \cap C'D' = E' \Rightarrow E' \in SE\) hay 3 điểm S, E, E’ thẳng hàng.

Chọn A.

Câu 6:

Cho đa giác lồi có n cạnh \(\left( n\ge 4 \right)\), các đường chéo của đa giác cắt nhau tạo thành bao nhiêu giao điểm, biết rằng không có ba đường thẳng nào đồng quy

Lời giải: