Bộ Đề Kiểm Tra Tham Khảo Học Kì II - Toán 11 - Kết Nối Tri Thức Với Cuộc Sống – Bộ Đề 01 - Đề 4
16 câu hỏi 60 phút
Cho \(a\) là một số dương, biểu thức \(\sqrt[3]{a^5} \sqrt{a^2}\) viết dưới dạng lũy thừa với số mũ hữu tỉ là?
\(a^{\frac{5}{6}}\)
\(a^{\frac{7}{6}}\)
\(a^{\frac{3}{4}}\)
\(a^{\frac{6}{5}}\)
Với \(a>0\), ta có \(\sqrt[3]{a^5} \sqrt{a^2} = a^{\frac{5}{3}} a^{\frac{2}{2}} = a^{\frac{5}{3}} a^{1} = a^{\frac{5}{3}+1} = a^{\frac{2+3}{6}} = a^{\frac{7}{6}}\).
Danh sách câu hỏi:
Với \(a>0\), ta có \(\sqrt[3]{a^5} \sqrt{a^2} = a^{\frac{5}{3}} a^{\frac{2}{2}} = a^{\frac{5}{3}} a^{1} = a^{\frac{5}{3}+1} = a^{\frac{2+3}{6}} = a^{\frac{7}{6}}\).
Đồ thị hàm số ở hình vẽ là đồ thị của hàm số mũ có dạng \(y = a^x\). Loại đáp án A.
Dựa vào đồ thị ta thấy hàm số nghịch biến trên \(\mathbb{{R}}\) nên \(0<a<1\). Loại đáp án B, D.
Vậy đồ thị trong hình vẽ là đồ thị hàm số \(y = (\frac{1}{3})^x\).
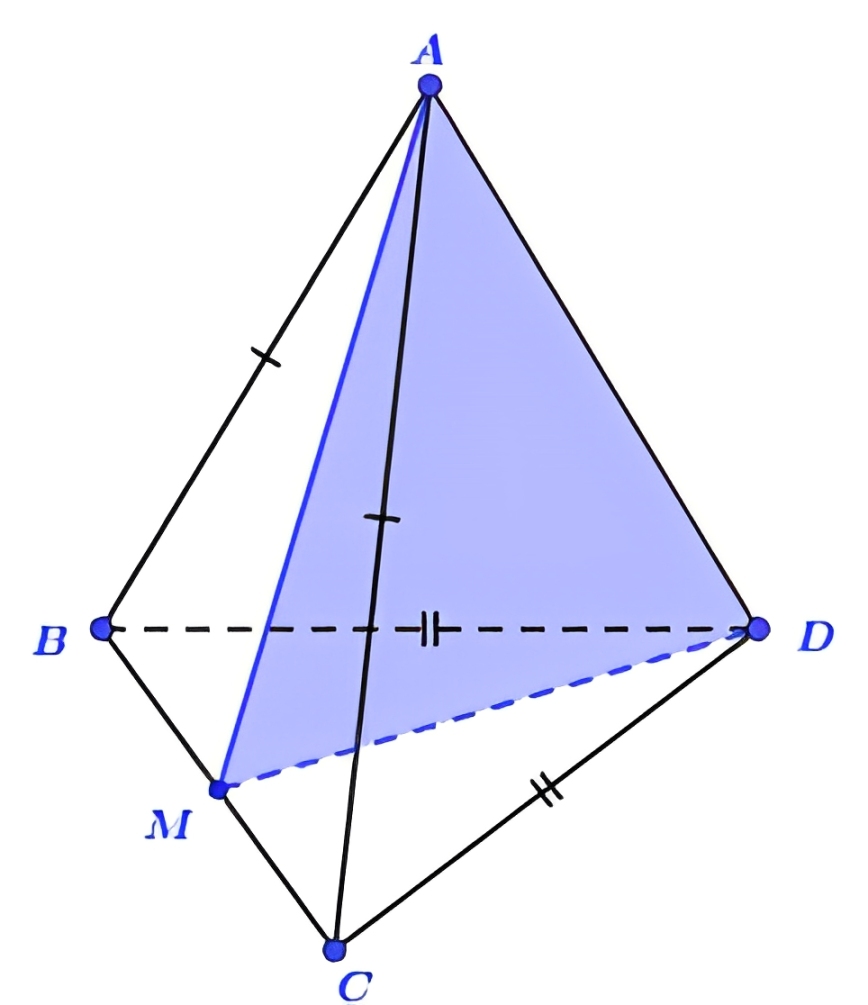
Gọi \(M\) là trung điểm \(BC\). Do tam giác \(ABC\) cân tại \(A\) và tam giác \(DBC\) cân tại \(D\) nên, có:
\(\left\{ \begin{array}{l}AM \perp BC \\DM \perp BC\end{array} \right.\) \(\Rightarrow BC \perp (ADM) \Rightarrow BC \perp AD\).
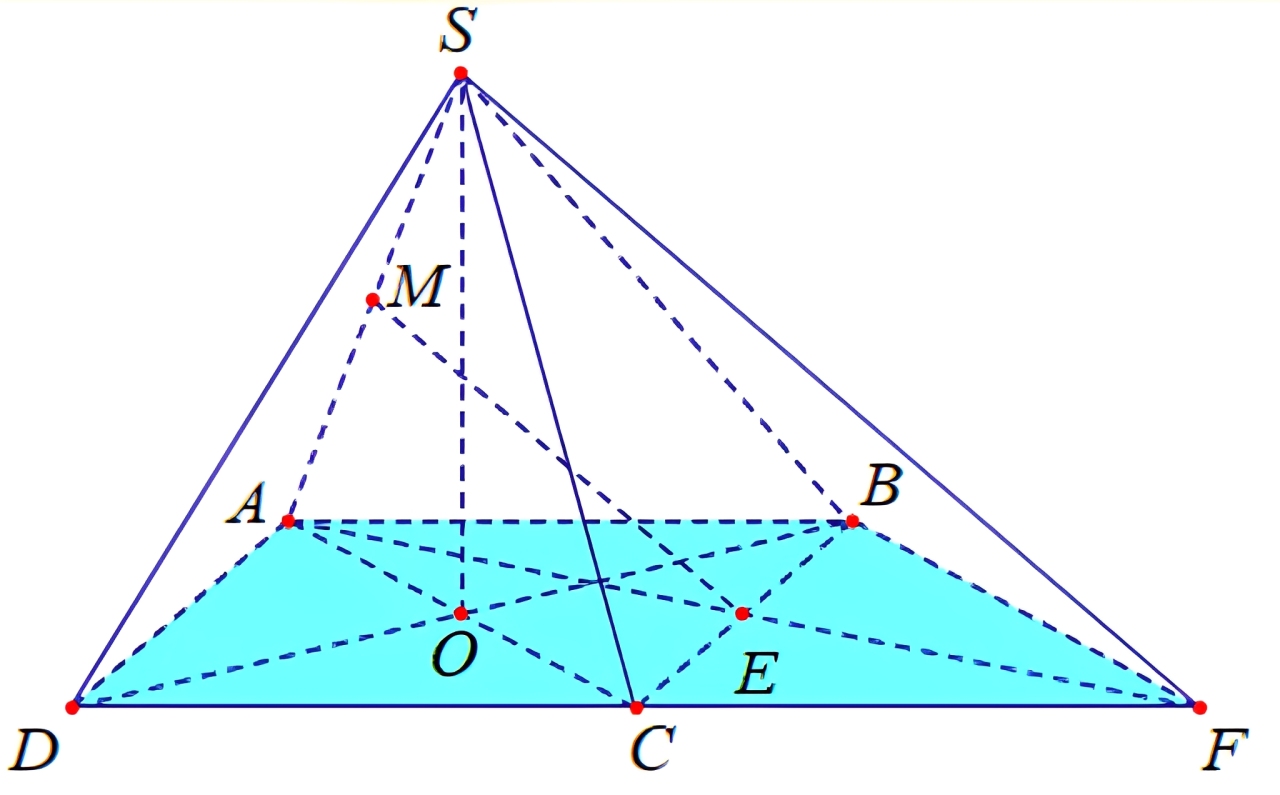
Dựng hình bình hành \(ABFC\).
Ta có \(EM // SF\) nên góc giữa \(EM\) và \((SBD)\) bằng góc giữa \(SF\) và \((SBD)\).
\(FB // AC \Rightarrow FB \perp (SBD)\) do đó góc giữa \(SF\) và \((SBD)\) bằng góc \(\widehat{{FSB}}\).
Ta có \(\tan \widehat{{FSB}} = \frac{BF}{SB} = \frac{AC}{SB} = \sqrt{2}\). Vậy chọn D.
Ta có \(\begin{cases} ({SAB}) \perp ({ABCD}) \\ ({SAD}) \perp ({ABCD}) \end{cases}\) nên \(SA \perp ({ABCD})\)
Suy ra \(SA \perp AC\) (B đúng); \(SA \perp BC\); \(SA \perp BD\).
Mặt khác \(BC \perp AB\) nên \(BC \perp ({SAB})\) suy ra \(BC \perp AH\) (A đúng).
và \(BD \perp AC\) nên \(BD \perp ({SAC})\) suy ra \(BD \perp SC\);
Đồng thời \(HK // BD\) nên \(HK \perp SC\) (C đúng).
Vậy mệnh đề sai là \(AK \perp BD\) (vì không đủ điều kiện chứng minh).
Câu 13:
Theo kết quả khảo sát ở một trường học về số học sinh yêu thích một loại nước giải khát A được cho bởi bảng sau:
Xác suất để chọn được một học sinh nam và một học sinh nữ ở khối lớp 11 mà thích uống nước giải khát A là \(\frac{952}{4565}\)
Xác suất để chọn được một học sinh nam ở lớp 11A và một học sinh nam ở lớp 11B không thích nước giải khát A là \(\frac{1}{2739}\)
Gọi \(A\) là biến cố: "Học sinh nam thích nước giải khát \(A\) ". Tính được \(P(A) = \frac{42}{79}\)
Việc thích uống nước giải khát A có phụ thuộc vào giới tính
Câu 14:
Cho hình chóp S.ABC có \(SA \perp (ABC)\), tam giác ABC vuông tại B (tham khảo hình vẽ).
Các mệnh đề sau đúng hay sai?
Khoảng cách từ C đến mặt phẳng \(({SAB})\) là đoạn BC
\(BC \perp ({SAB})\)
Khoảng cách từ B đến mặt phẳng \(({SAC})\) là đoạn AB
\(SB \perp BC\)