Bộ Đề Kiểm Tra Tham Khảo Học Kì II - Toán 11 - Kết Nối Tri Thức Với Cuộc Sống – Bộ Đề 01 - Đề 1
16 câu hỏi 60 phút
Biểu thức \(T = \sqrt[5]{a \cdot \sqrt[3]{a}}\). Viết \(T\) dưới dạng lũy thừa của số mũ hữu tỷ
\(a^{\frac{1}{3}}\)
\(a^{\frac{1}{5}}\)
\(a^{\frac{1}{15}}\)
\(a^{\frac{4}{15}}\)
\(T=\sqrt[5]{a \cdot \sqrt[3]{a}}=\sqrt[5]{a \cdot a^{\frac{1}{3}}}=\sqrt[5]{a^{\frac{4}{3}}}=a^{\frac{4}{15}}\).
Danh sách câu hỏi:
Câu 1:
Biểu thức \(T = \sqrt[5]{a \cdot \sqrt[3]{a}}\). Viết \(T\) dưới dạng lũy thừa của số mũ hữu tỷ
\(T=\sqrt[5]{a \cdot \sqrt[3]{a}}=\sqrt[5]{a \cdot a^{\frac{1}{3}}}=\sqrt[5]{a^{\frac{4}{3}}}=a^{\frac{4}{15}}\).
Hàm số \(y = a^{x}\) đồng biến khi \(a>1\) và nghịch biến khi \(0<a<1\).
Suy ra hàm số \(y = (\sqrt{2})^{x}\) đồng biến trên \(\mathbb{{R}}\) .
Do tam giác \(ABC\) đều nên \(CM \perp AB\), vì \(SA \perp (ABC)\) nên \(SA \perp CM \Rightarrow CM \perp (SAB)\)
\(\Rightarrow CM \perp SB\), \(CM \perp AN\) nên B, C đúng.
Do \(MN//SA\) nên \(MN \perp (ABC) \Rightarrow MN \perp MC\) nên D đúng.
Vậy A sai.
Ta có \((AC', (ABC)) = (AC', AC) = \widehat{C'AC}\), \(\tan \widehat{C'AC} = \dfrac{CC'}{AC} = \dfrac{AA'}{AB} = \dfrac{1}{\sqrt{3}}\) (Do ABC đều nên \(AC=AB=\sqrt{3}\))
\(\Rightarrow \widehat{C'AC} = 30^\circ\).
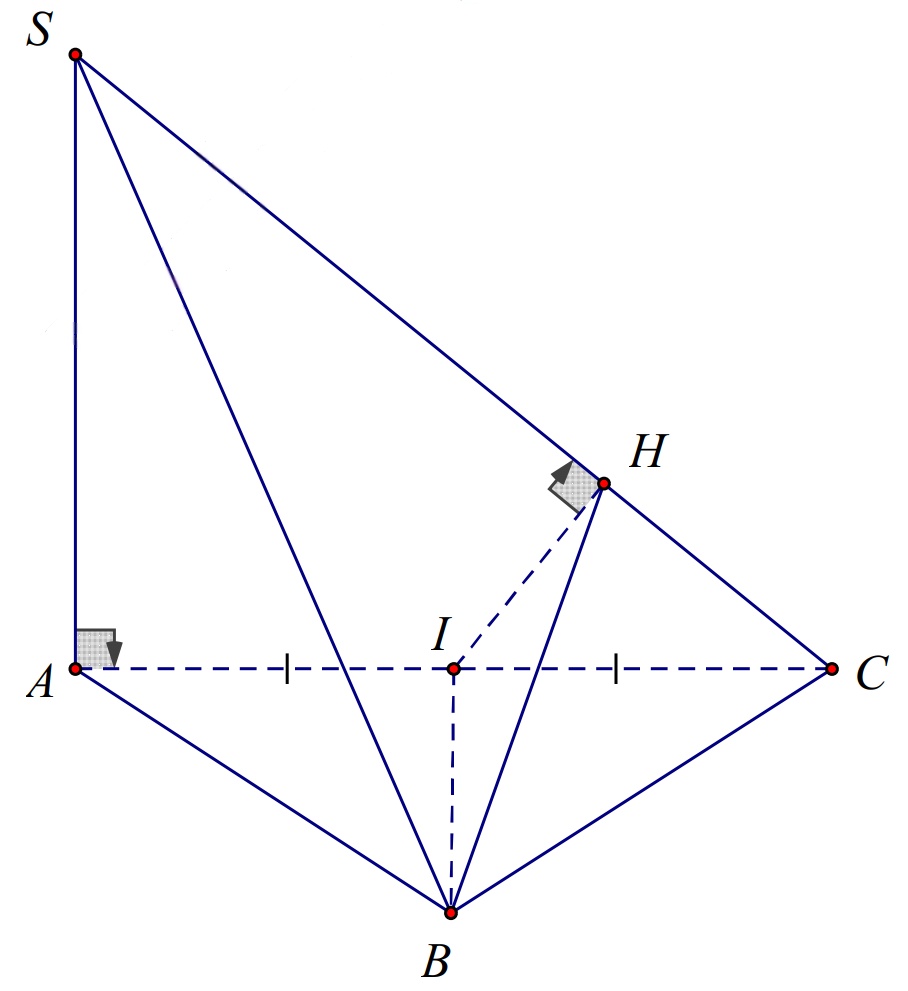
Ta có:
\(\begin{cases} BI \perp AC \text{ (gt)} \\ BI \perp SA \text{ (vì } SA \perp (ABC)) \end{cases} \Rightarrow BI \perp (SAC) \Rightarrow BI \perp SC\) (1).
Theo giả thiết: \(SC \perp IH\) (2).
Từ (1) và (2) suy ra: \(SC \perp (BIH)\). Mà \(SC \subset (SBC)\) nên \((BIH) \perp (SBC)\).
Câu 13:
Xét khối tứ diện \(A B C D\) có cạnh \(A B=x\), các cạnh còn lại đều bằng \(2 \sqrt{3}\). Các mệnh đề sau đúng hay sai?
Diện tích tam giác \(B C D\) bằng \(S_{B C D}=3 \sqrt{3}\)
\(V_{A B C D}=\frac{\sqrt{3}}{3} x \sqrt{36-x^{2}}\)
Khi \(x=3\) thì \(V=\frac{9}{4}\)
Khi \(x=3 \sqrt{2}\) thì thể tích khối tứ diện \(A B C D\) đạt giá trị lớn nhất
Câu 14:
Cho hàm số \(y=\sin ^{2} x\). Các mệnh đề sau đúng hay sai?
\(2 y^{\prime}+y^{\prime \prime}=\sqrt{2} \cos \left(2 x-\frac{\pi}{4}\right)\)
\(2 y+y^{\prime} \cdot \tan x=0\)
\(4 y-y^{\prime \prime}=2\)
\(4 y^{\prime}+y^{\prime \prime \prime}=0\)