Bộ Đề Kiểm Tra Tham Khảo Học Kì II - Toán 11 - Kết Nối Tri Thức Với Cuộc Sống – Bộ Đề 01 - Đề 3
16 câu hỏi 60 phút
Rút gọn biểu thức \(P = x^3.\sqrt{x}\), với \(x\) là số thực dương
\(P = x^{\frac{1}{12}}\)
\(P = x^{\frac{7}{12}}\)
\(P = x^{\frac{2}{3}}\)
\(P = x^{\frac{7}{2}}\)
\(P = x^3.\sqrt{x} = x^3.x^{\frac{1}{2}} = x^{3+\frac{1}{2}} = x^{\frac{7}{2}}\).
Danh sách câu hỏi:
\(P = x^3.\sqrt{x} = x^3.x^{\frac{1}{2}} = x^{3+\frac{1}{2}} = x^{\frac{7}{2}}\).
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số nhận đường thẳng \(x = −1\) làm tiệm cận đứng nên loại đáp án A và C.
Lại có \(A(2;1)\) thuộc đồ thị hàm số nên loại phương án B.
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
Dễ thấy \(CB \perp (SAB) \Rightarrow SB\) là hình chiếu vuông góc của \(SC\) lên \((SAB)\).
Vậy góc giữa đường thẳng \(SC\) và mặt phẳng \((SAB)\) là \(\widehat{{CSB}}\).
Tam giác \(CSB\) có \(\widehat{{B}} = 90^\circ;CB = a; SB = a\sqrt{3} \Rightarrow \tan \widehat{{CSB}} = \frac{{CB}}{{SB}} = \frac{{a}}{{a\sqrt{3}}} = \frac{{1}}{{\sqrt{3}}}\).
Vậy \(\widehat{{CSB}} = 30^\circ\).
Câu 5:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(SA = SC\). Khẳng định nào sau đây đúng?
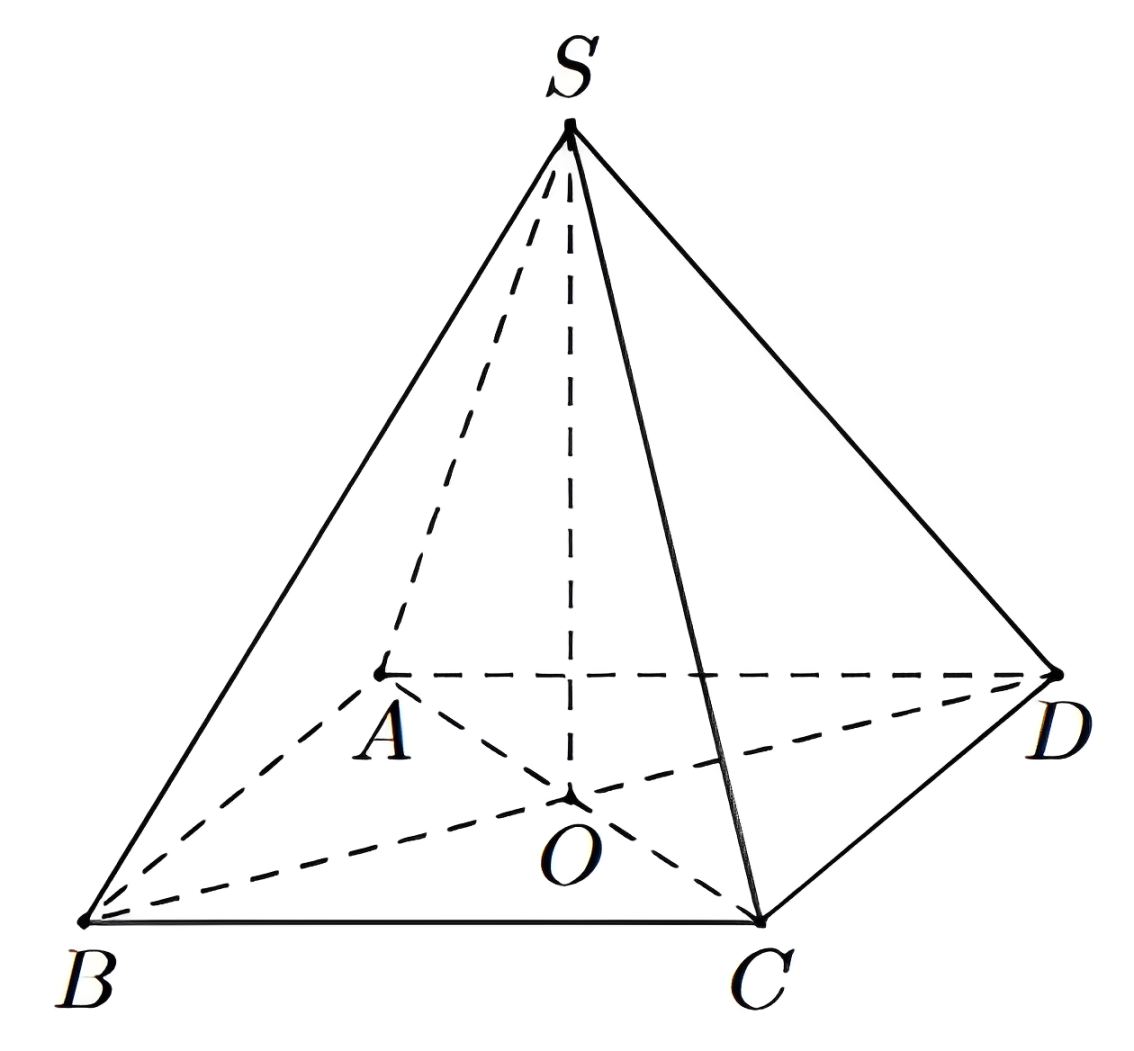
Gọi \(O = AC \cap BD\).
Tứ giác \(ABCD\) là hình thoi nên \(AC \perp BD\) \((1)\).
Mặt khác tam giác \(SAC\) cân tại \(S\) nên \(SO \perp AC\) \((2)\).
Từ \((1)\) và \((2)\) suy ra \(AC \perp (SBD)\) nên \((SBD) \perp (ABCD)\).
Câu 13:
Cho hình chóp \(S.ABCD\) có \(SC = x\) \((0<x<\sqrt{3})\), các cạnh còn lại đều bằng \(1\) (tham khảo hình vẽ). Biết rằng thể tích khối chóp \(S.ABCD\) lớn nhất khi và chỉ khi \(x = \frac{{\sqrt{a}}}{{b}}\) \((a, b \in \mathbb{{Z}}^*)\). Các mệnh đề sau đúng hay sai?
\(a^2 - 2b < 30\)
\(a^2 - 8b = 20\)
\(b^2 - a < -2\)
\(2a - 3b^2 = -1\)
Câu 14:
Cho hàm số \(y = x[\cos(\ln x) + \sin(\ln x)]\). Các mệnh đề sau đúng hay sai?
\(x^2y'' + xy' - 2y = 0\)
\(x^2y'' + xy' - 2y = 0\)
\(x^2y'' + xy' - 2y = 0\)
\(x^2y' - xy'' + 2y = 0\)