Bộ Đề Kiểm Tra Tham Khảo Học Kì II - Toán 11 - Kết Nối Tri Thức Với Cuộc Sống – Bộ Đề 01 - Đề 2
16 câu hỏi 60 phút
Rút gọn biểu thức \(P = x^{\frac{1}{3}} \cdot \sqrt[6]{x}\) với \(x > 0\)
\(P = \sqrt{x}\)
\(P = x^{\frac{5}{6}}\)
\(P = x^{2}\)
\(P = x^{\frac{2}{3}}\)
Với \(x > 0\), ta có \(P = x^{\frac{1}{3}}.x^{\frac{1}{6}} = x^{\frac{1}{3}+\frac{1}{6}}= x^{\frac{2}{6}+\frac{1}{6}} = x^{\frac{3}{6}} = x^{\frac{1}{2}} = \sqrt{x}\).
Danh sách câu hỏi:
Với \(x > 0\), ta có \(P = x^{\frac{1}{3}}.x^{\frac{1}{6}} = x^{\frac{1}{3}+\frac{1}{6}}= x^{\frac{2}{6}+\frac{1}{6}} = x^{\frac{3}{6}} = x^{\frac{1}{2}} = \sqrt{x}\).
Điều kiện: \(4x – x^{2} > 0 \Leftrightarrow 0 < x < 4\).
Vậy: Tập xác định là \(\mathscr{{D}} = (0;4)\).
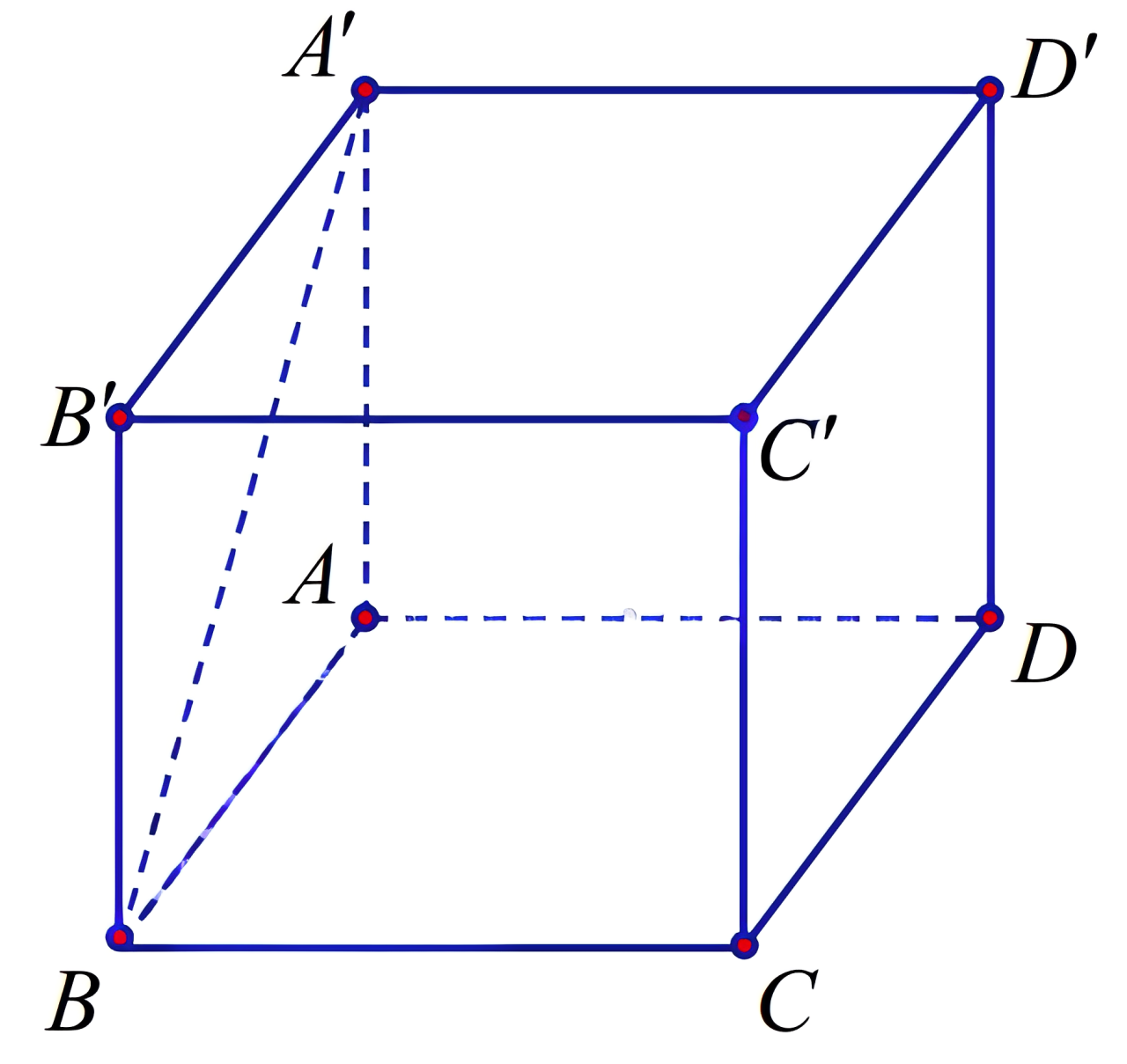
Có \(CD \parallel AB \Rightarrow (BA',CD) = (BA',BA) = \widehat{{ABA'}} = 45^\circ\) (do \(ABB'A'\) là hình vuông).
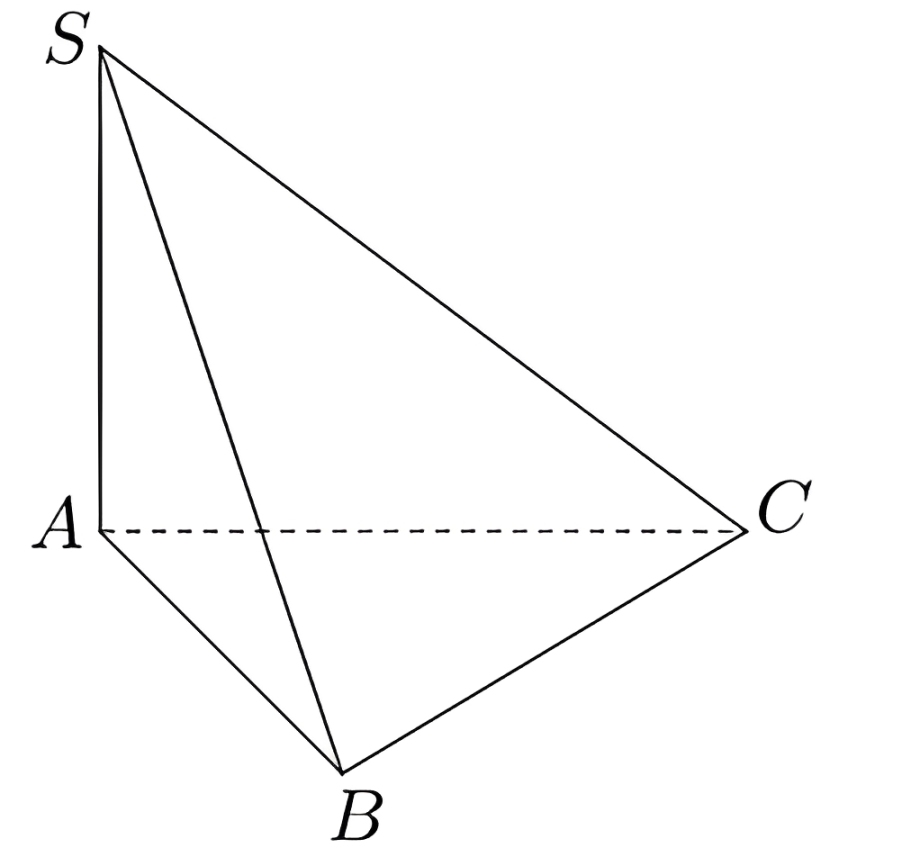
Góc giữa đường thẳng \(SC\) và mặt phẳng \((ABC)\) là góc \(\widehat{{SCA}}\).
Tam giác \(SAC\) vuông cân tại \(A\) nên góc \(\widehat{{SCA}} = 45^\circ\).
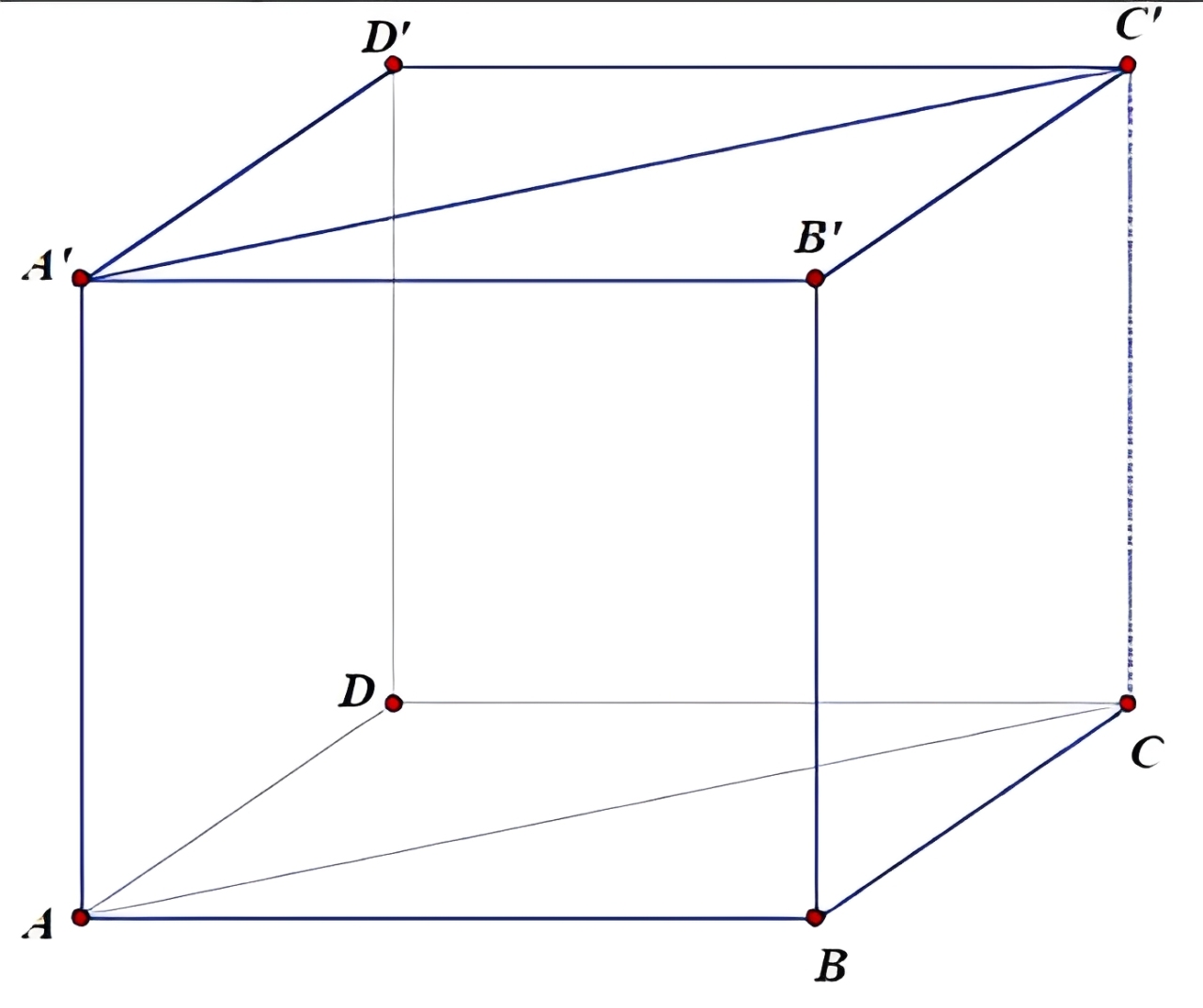
\(Do \; AA' \perp (ABCD) \Rightarrow (ACC'A') \perp (ABCD)\).
Câu 13:
Một trường học có tỉ lệ học sinh nam và nữ là 5:3. Trong đó, tỉ lệ số học sinh nam thuận tay trái là \(11\%\), tỉ lệ số học sinh nữ thuận tay trái là \(9\%\). Khi đó:
Xác suất để chọn được 1 học sinh nam ở trường không thuận tay trái là: \(\frac{273}{800}\)
Xác suất để chọn được 1 học sinh nữ ở trường không thuận tay trái là: \(\frac{89}{160}\)
Xác suất để chọn được 1 học sinh nam, 1 học sinh nữ ở trường thuận tay trái lần lượt là: \(\frac{11}{160}\) và \(\frac{27}{800}\)
Xác suất để chọn ngẫu nhiên 5 học sinh ở trường trong đó có đúng 1 học sinh nam và 1 học sinh nữ thuận tay trái là: \(\frac{297}{128000}\)
Câu 14:
Cho hàm số \(f(x) = 3^{2x} -2.3^{x}\) có đồ thị như hình vẽ sau:
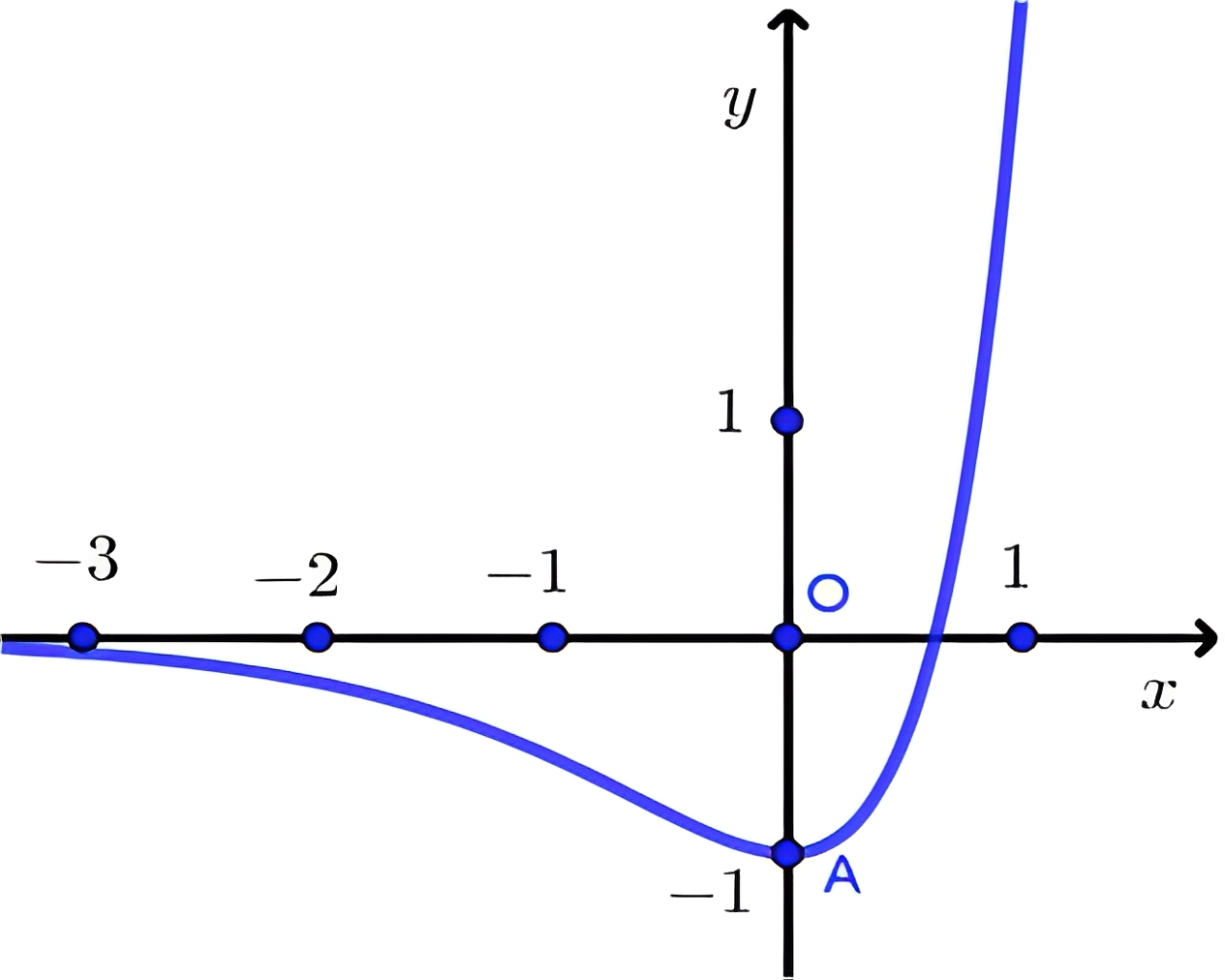
Đường thẳng \(y = 0\) cắt đồ thị hàm số \((C)\) tại điểm có hoành độ là \(x = \log_{3} 2\)
Bất phương trình \(f (x) \geqslant -1\) có nghiệm duy nhất
Bất phương trình \(f(x) \geqslant 0\) có tập nghiệm là: \((-\infty;\log_{3} 2)\)
Đường thẳng \(y = 0\) cắt đồ thị hàm số \((C)\) tại 2 điểm phân biệt