Trắc nghiệm Cấp số cộng Toán Lớp 11
-
Câu 1:
Trong hội chợ tết, một công ty sữa muốn xếp 900 hộp sữa theo số lượng 1, 3, 5, ... từ trên xuống dưới (số hộp sữa trên mỗi hàng xếp từ trên xuống là các số lẻ liên tiếp - mô hình như hình bên). Hàng dưới cùng có bao nhiêu hộp sữa?
.png)
A. 59
B. 30
C. 61
D. 57
-
Câu 2:
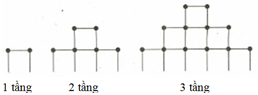
Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp được tháp có 10 tầng thì bạn An cần đúng bao nhiêu que diêm?
A. 210
B. 39
C. 100
D. 270
-
Câu 3:
Cho cấp số cộng (un) có tất cả các số hạng đều dương thoả mãn \({u_1} + {u_2} + ... + {u_{2018}} = 4\left( {{u_1} + {u_2} + ... + {u_{1009}}} \right)\). Giá trị nhỏ nhất của biểu thức \(P = \log _3^2{u_2} + \log _3^2{u_5} + \log _3^2{u_{14}}\) bằng
A. 3
B. 1
C. 2
D. 4
-
Câu 4:
Cho cấp số cộng (un) có các số hạng đều dương, số hạng đầu u1 = 1 và tổng của 100 số hạng đầu tiên bằng 14950. Tính giá trị của tổng \(S = \frac{1}{{{u_2}\sqrt {{u_1}} + {u_1}\sqrt {{u_2}} }} + \frac{1}{{{u_3}\sqrt {{u_2}} + {u_2}\sqrt {{u_3}} }} + ... + \frac{1}{{{u_{2018}}\sqrt {{u_{2017}}} + {u_{2017}}\sqrt {{u_{2018}}} }}\)
A. \(\frac{1}{3}\left( {1 - \frac{1}{{\sqrt {6052} }}} \right)\)
B. \(1 - \frac{1}{{\sqrt {6052} }}\)
C. 2018
D. 1
-
Câu 5:
Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi rạp hát có tất cả bao nhiêu ghế?
A. 1635
B. 1792
C. 2055
D. 3125
-
Câu 6:
Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là:
A. \(\frac{1}{2};{\rm{\;}}1;{\rm{\;}}\frac{3}{2}.\)
B. \(\frac{1}{3};{\rm{\;}}1;{\rm{\;}}\frac{5}{3}.\)
C. \(\frac{3}{4};{\rm{\;}}1;{\rm{\;}}\frac{5}{4}.\)
D. \(\frac{1}{4};{\rm{\;}}1;{\rm{\;}}\frac{7}{4}.\)
-
Câu 7:
Phương trình \({x^4} - 2\left( {m + 1} \right){x^2} + 2m + 1 = 0\) (1) có bốn nghiệm phân biệt lập thành cấp số cộng
A. m = 2 hoặc \(m = - \frac{4}{9}\)
B. m = 4 hoặc \(m = - \frac{4}{9}\)
C. m =4 hoặc m = -2
D. m = 3 hoặc m=-1
-
Câu 8:
Tìm m để phương trình \({x^3} - 3{x^2} - 9x + m = 0\) có ba nghiệm phân biệt lập thành cấp số cộng.
A. m = 16
B. m = 11
C. m = 13
D. m = 12
-
Câu 9:
Tìm x biết \({x^2} + 1,x - 2,1 - 3x\) lập thành cấp số cộng ;
A. x = 4, x = 3
B. x = 2, x = 3
C. x = 2, x = 5
D. x = 2, x = 1
-
Câu 10:
Tìm x để 3 số : 1-x; x2 ; x+1 theo thứ tự lập thành một cấp số cộng?
A. Không có giá trị nào của x
B. x = ±2
C. x = ±1
D. x = 0
-
Câu 11:
Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A. \({a^2} + {c^2} = 2ab + 2bc\)
B. \({a^2} - {c^2} = 2ab - 2bc\)
C. \({a^2} + {c^2} = 2ab - 2bc\)
D. \({a^2} - {c^2} = ab - bc\)
-
Câu 12:
Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có góc nhỏ nhất bằng 25o. Tìm 2 góc còn lại?
A. 650, 900
B. 750, 800
C. 600, 950
D. 550, 1000
-
Câu 13:
Ba số hạng liên tiếp của một cấp số cộng có tổng bằng -9 và tổng các bình phương của chúng bằng 29. Tìm số hạng đầu tiên
A. - 3 hoặc – 6
B. – 4 hoặc -2
C. - 1 hoặc - 5
D. - 4 hoặc - 7
-
Câu 14:
Cho cấp số cộng (un) thỏa mãn \(\left\{ {\begin{array}{*{20}{l}}
{{u_5} + 3{u_3} - {u_2} = - 21}\\
{3{u_7} - 2{u_4} = - 34}
\end{array}} \right.\)Tính tổng 15 số hạng đầu của cấp số
A. - 244
B. - 274
C. - 253
D. - 285
-
Câu 15:
Cho cấp số cộng (un) thỏa mãn \(\left\{ {\begin{array}{*{20}{l}}
{{u_5} + 3{u_3} - {u_2} = - 21}\\
{3{u_7} - 2{u_4} = - 34}
\end{array}} \right.\)Tính số hạng thứ 100 của cấp số
A. - 243
B. - 295
C. - 231
D. - 294
-
Câu 16:
Cho hai cấp số cộng (un): 4,7,10,13,16,...và (vn): 1,6,11,16,21,... Hỏi trong 100 số hạng đầu tiên của mỗi cấp số cộng , có bao nhiêu số hạng chung?
A. 10
B. 20
C. 30
D. 40
-
Câu 17:
Cho cấp số cộng (un) thỏa \(\left\{ {\begin{array}{*{20}{c}}
{{u_2} - {u_3} + {u_5} = 10}\\
{{u_4} + {u_6} = 26}
\end{array}} \right.\)Tính \(S = {u_1} + {u_4} + {u_7} + ... + {u_{2011}}\)
A. S = 673015
B. S = 6734134
C. S = 673044
D. S = 141
-
Câu 18:
Cho cấp số cộng (un) thỏa \(\left\{ {\begin{array}{*{20}{c}}
{{u_2} - {u_3} + {u_5} = 10}\\
{{u_4} + {u_6} = 26}
\end{array}} \right.\)Xác định công thức tổng quát của cấp số
A. \({u_n} = 3n - 2\)
B. \({u_n} = 3n - 4\)
C. \({u_n} = 3n - 3\)
D. \({u_n} = 3n - 1\)
-
Câu 19:
Cho cấp số cộng (un) có: u1 = −0,1;d = 0,1. Số hạng thứ 7 của cấp số cộng này là:
A. 1,6
B. 6
C. 0,5
D. 0,6
-
Câu 20:
Cho 4 số lập thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :
A. 22
B. 166
C. 1752
D. 1408
-
Câu 21:
Cho một cấp số cộng có \({u_1} = - 3;\,\,{u_6} = 27\). Tìm d ?
A. d = 5
B. d = 7
C. d = 6
D. d = 8
-
Câu 22:
Cho cấp số cộng có 8 số hạng. Số hạng đầu bằng 3 số hạng cuối bằng 24. Tính tổng các số hạng này
A. 105
B. 27
C. 108
D. 111
-
Câu 23:
Dãy số (un) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai d, biết rẳng \({u_n} = \frac{2}{n}\)
A. d = Ø
B. \(d = \frac{1}{2}\)
C. d = - 3
D. d = 1
-
Câu 24:
Dãy số (un) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai d, biết rẳng un = n2+1
A. d = ø
B. d = 3
C. d = - 3
D. d = 1
-
Câu 25:
Dãy số (un) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai d, biết rẳng un = −3n+1
A. d = - 2
B. d = 3
C. d = - 3
D. d = 1
-
Câu 26:
Dãy số (un) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai d, biết rẳng un = 2n+3
A. d = - 2
B. d = 3
C. d = 5
D. d = 2
-
Câu 27:
Cho phương trình: \({x^3}\; + \;3{x^2}\;--\;\left( {24 + m} \right)x\; - 26\;--n = \;0.\). Tìm hệ thức liên hệ giữa m và n để 3 nghiệm phân biệt x1, x2, x3 lập thành một cấp số cộng
A. 3m = n
B. m = 3n
C. m = n
D. m + n = 0
-
Câu 28:
Cho một dãy số có các số hạng đầu tiên là 1,8,22,43...Hiệu của hai số hạng liên tiếp của dãy số đó lập thành một cấp số cộng: 7,14,21,...,7n. Số 35351 là số hạng thứ bao nhiêu của dãy số đã cho?
A. 57
B. 80
C. 101
D. 200
-
Câu 29:
Giá tiền công khoan giếng ở cơ sở A được tinh như sau: giá của mét khoan đầu tiên là 8000 đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng lên 500 đồng so với giá của mét khoan ngay trước nó. Vậy muốn khoan 20 mét thì mất bao nhiêu đồng?
A. 200000 đồng
B. 255000 đồng
C. 285000 đồng
D. 315000 đồng
-
Câu 30:
Người ta trồng 3003 cây theo hình tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ 2 có 2 cây, hàng thứ 3 có 3 cây,...Vậy có tất cả bao nhiêu hàng?
A. 75
B. 76
C. 77
D. 78
-
Câu 31:
Xen vào giữa hai số 4 và 40 bốn số để được một cấp số cộng có công sai lớn hơn 3. Tìm tỏng 4 số đó.
A. 88
B. 92
C. 128
D. 132
-
Câu 32:
Xác định số đo góc nhỏ nhất của một tứ giác lồi, biết rằng số đo 4 góc lập thành một cấp số cộng và góc lớn nhất bằng 5 lần góc nhỏ nhất.
A. 300
B. 450
C. 150
D. 600
-
Câu 33:
Số hạng đầu tiên của cấp số cộng dương (un) thoả mãn :
\(\left\{ {\begin{array}{*{20}{l}}
{{u_7} - {u_3} = 8}\\
{{u_2}{u_7} = 75}
\end{array}} \right.\)A. 2
B. 3
C. 4
D. 5
-
Câu 34:
Công sai của cấp số cộng (un) thoả mãn : \(\left\{ {\begin{array}{*{20}{l}}
{{u_1} + {u_5} - {u_3} = 10}\\
{{u_1} + {u_6} = 17}
\end{array}} \right.\) làA. 0
B. - 1
C. - 2
D. - 3
-
Câu 35:
Mặt sang tầng một ngôi nhà cao hơn mặt sân 0,5m. Cầu thang đi tầng 1 lên tầng 2 gồm 21 bậc, mỗi bậc cao 18cm. Độ cao của tầng hai so với mặt sân là:
A. 4,10m
B. 4,28m
C. 1,89m
D. 1,8m
-
Câu 36:
Cho hai cấp số cộng (un): 4,7,10,13,16,...và (vn): 1,6,11,16,21,... Hỏi trong 100 số hạng đầu tiên của mỗi cấp số cộng , có bao nhiêu số hạng chung?
A. 10
B. 20
C. 30
D. 40
-
Câu 37:
Tìm x biết 1+3 +5+...+x = 64
A. 9
B. 11
C. 15
D. 17
-
Câu 38:
Với mỗi số nguyên dương, gọi An là giao điểm của (d) và đường thẳng x = n. Xét dãy số (un) với un là tung độ của điểm An. Tính u1+...+u15.
A. 405
B. 305
C. 205
D. 105
-
Câu 39:
Cho 4 số lập phương thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :
A. 22
B. 166
C. 1752
D. 1408
-
Câu 40:
Cho cấp số cộng có 8 số hạng. Số hạng đầu bằng 3 số hạng cuối bằng 24. Tính tổng các số hạng này
A. 105
B. 27
C. 108
D. 111
-
Câu 41:
Tìm m để phương trình \(x^{3}-3 x^{2}-9 x+m=0\) có ba nghiệm phân biệt lập thành cấp số cộng
A. m=16
B. m=11
C. m=13
D. m=12
-
Câu 42:
Tìm x, y biết các số \(x+5 y, 5 x+2 y, 8 x+y\) lập thành cấp số cộng và các số \((y-1)^{2}, x y-1,(x+1)^{2}\) lập thành cấp số nhân.
A. \((x ; y)=\left(-\sqrt{3} ; \frac{3}{2}\right) ;\left(\sqrt{3} ; \frac{\sqrt{3}}{2}\right)\)
B. \((x ; y)=\left(\sqrt{3} ;-\frac{\sqrt{3}}{2}\right) ;\left(-\sqrt{3} ;-\frac{\sqrt{3}}{2}\right)\)
C. \((x ; y)=\left(\sqrt{3} ; \frac{\sqrt{3}}{2}\right) ;\left(\sqrt{3} ; \frac{\sqrt{3}}{2}\right)\)
D. \((x ; y)=\left(-\sqrt{3} ;-\frac{\sqrt{3}}{2}\right) ;\left(\sqrt{3} ; \frac{\sqrt{3}}{2}\right)\)
-
Câu 43:
Tìm x biết \(x^{2}+1, x-2,1-3 x\) lập thành cấp số cộng .
A. x=4, x=3
B. x=2, x=3
C. x=2, x=5
D. x=2, x=1
-
Câu 44:
Xác định a để 3 số \(1+3 a ; a^{2}+5 ; 1-a\) theo thứ tự lập thành một cấp số cộng?
A. Không có giá trị nào của a .
B. \(a=0\)
C. \(a=\pm 1\)
D. \(a=\pm \sqrt{2}\)
-
Câu 45:
Xác định x để 3 số \(1+2 x ; 2 x^{2}-1 ;-2 x\) theo thứ tự lập thành một cấp số cộng?
A. \(x=\pm 3\)
B. \(x=\pm \frac{\sqrt{3}}{2}\)
C. \(x=\pm \frac{\sqrt{3}}{4}\)
D. Không có giá trị nào của x.
-
Câu 46:
Xác định x để 3 số \(1-x ; x^{2} ; 1+x\) theo thứ tự lập thành một cấp số cộng?
A. Không có giá trị nào của x .
B. \(x=\pm 2\)
C. \(x=\pm 1\)
D. x=0
-
Câu 47:
Cho a, b, c theo thứ tự lập thành cấp số cộng, ba số nào dưới đây cũng lập thành một cấp số cộng ?
A. \(2 b^{2}, a, c^{2}\)
B. \(-2 b,-2 a,-2 c\)
C. \(2 b, a, c\)
D. \(2 b,-a,-c\)
-
Câu 48:
Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?
A. \(a^{2}+c^{2}=2 a b+2 b c\)
B. \(a^{2}-c^{2}=2 a b-2 b c\)
C. \(a^{2}+c^{2}=2 a b-2 b c\)
D. \(a^{2}-c^{2}=a b-b c\)
-
Câu 49:
Tam giác ABC có ba góc \(\hat A,\hat B,\hat C\) theo thứ tự đó lập thành cấp số cộng và \(\hat C= 5\hat A\) . Xác định số đo các góc \(\hat A,\hat B,\hat C\)
A. \(\begin{aligned} &\left\{\begin{array}{l} \hat A=10^{\circ} \\ \hat B=120^{\circ} \\ \hat C=50^{\circ} \end{array}\right. \end{aligned}\)
B. \(\left\{\begin{array}{l} \hat A=15^{\circ} \\ \hat B=105^{\circ} \\ \hat C=60^{\circ} \end{array}\right.\)
C. \(\begin{aligned} &\left\{\begin{array}{l} \hat A=5^{0} \\ \hat B=60^{\circ} \\ \hat C=25^{\circ} \end{array}\right. \end{aligned}\)
D. \(\left\{\begin{array}{l} \hat A=20^{\circ} \\ \hat B=60^{\circ} \\ \hat C=100^{\circ} \end{array}\right.\)
-
Câu 50:
Cho cấp số cộng \((u_n)\) có công sai d>0; \(\left\{\begin{array}{l} u_{31}+u_{34}=11 \\ u_{31}^{2}+u_{34}^{2}=101 \end{array}\right.\). Hãy tìm số hạng tổng quát của cấp số cộng đó.
A. \(u_{n}=3 n-9\)
B. \(u_{n}=3 n-2\)
C. \(u_{n}=3 n-92\)
D. \(u_{n}=3 n-66\)














