Cho số phức (z ) thỏa mãn| z2 - 2z + 5| = | (z - 1 + 2i)(z + 3i - 1)|. Tìm giá trị nhỏ nhất của P =| w | với w = z - 2 + 2i
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có
\(\begin{array}{l} \left| {{z^2} - 2z + 5} \right| = \left| {\left( {z - 1 + 2i} \right)\left( {z + 3i - 1} \right)} \right|\\ \Leftrightarrow \left| {{{\left( {z - 1} \right)}^2} + 4} \right| = \left| {\left( {z - 1 + 2i} \right)} \right|\left| {\left( {z + 3i - 1} \right)} \right| \Leftrightarrow \left| {{{\left( {z - 1} \right)}^2} - {{\left( {2i} \right)}^2}} \right| = \left| {\left( {z - 1 + 2i} \right)} \right|\left| {\left( {z + 3i - 1} \right)} \right|\\ \Leftrightarrow |(z - 1 + 2i)(z - 1 - 2i)| = |(z - 1 + 2i)||(z + 3i - 1)| \to \left[ \begin{array}{l} z - 1 + 2i = 0(1)\\ |(z - 1 + 2i)| = |(z + 3i - 1)|(2) \end{array} \right. \end{array}\)
Từ \( \left( 1 \right) \Rightarrow z = 1 - 2i \Rightarrow w = - 1 \Rightarrow P = \left| w \right| = 1.\)
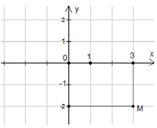
Xét (2). Gọi z=x+yi(x;y∈R).
Ta có:
\( \left| {\left( {z - 1 - 2i} \right)} \right| = \left| {\left( {z + 3i - 1} \right)} \right| \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = {\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} \Leftrightarrow y = - \frac{1}{2}.\)
Khi đó
\( w = x - \frac{1}{2}i - 2 + 2i = \left( {x - 2} \right) + \frac{3}{2}i \Rightarrow P = \left| w \right| = \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {\frac{3}{2}} \right)}^2}} \ge \frac{3}{2} > 1\)
Vậy Pmin=1.
Câu hỏi liên quan
-
Cho số phức z thỏa z = 1+ i+ i2+ i3+...+ i2016. Khi đó phần thực và phần ảo của z lần lượt là
-
Tính mô đun của số phức z biết \((1-2 i) z=2+3 i\)
-
Cho các số phức z thỏa mãn |z|= 4. Biết rằng tập hợp các điểm biểu diễn các số phức \(w=(3+4 i) z+i\) là một đường tròn. Tính bán kính r của đường tròn đó.
-
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và (1+i)z.
Tính \(\left| z \right|\) biết diện tích tam giác OAB bằng 8.
-
Cho các điểm A, B, C, trong mặt phẳng phức theo thứ tự được biểu diễn bởi các số phức: \(1+i ; 2+4 i ; 6+5 i\) i. Tìm số phức biểu diễn điểm D sao cho tứ giác ABDC là hình bình hành:
-
Phần thực và phần ảo của số phức z = 1+ 2i lần lượt là:
-
Cho số phức z thỏa mãn \(z + 4\bar z = 7 + i\left( {z - 7} \right)\). Khi đó, môđun của z bằng bao nhiêu
-
Giả sử z1 , z2 là hai nghiệm của phương trình z2 - 2z + 5 = 0 và A, B là các điểm biểu diễn của z1 , z2 . Tọa độ trung điểm I của đoạn thẳng AB là:
-
Tổng phần thực và phần ảo của số phức z thoả mãn \( iz + (1- i)\overline z = -2i\)
bằng -
Tìm giá trị nhỏ nhất của |z|, biết rằng z thỏa mãn điều kiện |(4 + 2i)(1 - i)z - 1| = 1 .
-
Tìm điểm M biểu diễn số phức \(z=i-2\)
-
Xét các số phức \(z=x+y i(x ; y \in \mathbb{R})\) có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình \((C):(x-1)^{2}+(y-2)^{2}=4\). Tìm tập hợp các điểm biểu diễn của số phức \(w=z+\bar{z}+2 i\)
-
Trong mặt phẳng tọa độ, tập hợp các điểm M(x;y) biểu diễn của số phức \(z=x+y i(x ; y \in \mathbb{R})\) thỏa mãn \(\frac{z+i}{z-i}\) là số thực là:
-
Cho hai số phức
\(z_{1}=3-2 i, z_{2}=-2+i\). Tìm mô đun của số phức \(z_{1}+z_{2}\) -
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Tìm môđun của số phức z .
-
Tính môđun của số phức z thỏa \(\frac{(1+2 i) z}{3-i}=\frac{1}{2}(1+i)^{2}\)
-
Trong mặt phẳng phức Oxy , các số phức z thỏa \(|z+2 i-1|=|z+i|\). Tìm số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1,3)
-
Cho số phức z = ( 3 - 2i)(1 + i) 2 . Môđun của \(w = iz + \overline z \) là
-
Biểu diễn hình học của số phức z = 2 -3i là điểm nào trong những điểm sau đây?
-
Cho số phức \(\bar z = 3 - 2i\). Tìm phần thực và phần ảo của z.
