ADMICRO
Cho các số phức z thỏa mãn |z−3+4i|=2 và cho số phức w=2z+1−i . Khi đó |w| có giá trị lớn nhất bằng bao nhiêu?
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo saiĐặt z=x+yi với x,y∈R . Khi đó |z−3+4i|=2⇔(x−3)2+(y+4)2=4 Goi M là điểm biểu diễn hình học của số phức z ta có M∈(I;2) với I(3;−4) . w=2z+1−i=2x+1+(2y−1)i⇒|w|=√(2x+1)2+(2y−1)2=√4[(x+12)2+(y−12)2]
Gọi A(−12;12) suy ra |w|=√4[(x+12)2+(y−12)2]=2AM Dễ thấy AI=√(3+12)2+(−4−12)2=√1302>2 nên A nằm ngoài (I;2) .
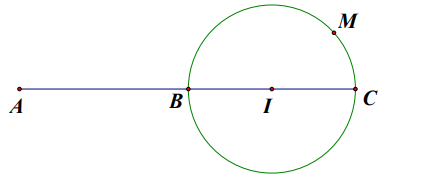
Có AM≤AC nên AMmax=AC.
Dấu “=” xảy ra khi và chỉ khi M≡C. Khi đó AC=AI+IC=√1302+2=√130+42
Vậy |w|max=2AC=√130+4 .
ZUNIA9
AANETWORK














