Trắc nghiệm Khoảng cách Toán Lớp 11
-
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, các cạnh bên của hình chóp bằng nhau và bằng 2a. Tính khoảng cách d từ A đến mặt phẳng ( SCD )
A. \( d = \frac{{a\sqrt 7 }}{{\sqrt {30} }}.\)
B. \( d = \frac{{2a\sqrt 7 }}{{\sqrt {30} }}.\)
C. \( d = \frac{{a\sqrt 7 }}{{\sqrt {3} }}.\)
D. \( d = \frac{{a\sqrt 7 }}{{\sqrt {32} }}.\)
-
Câu 2:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(AB = a,AC = a\sqrt 3\) . Tam giác SBC đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách d từ B đến mặt phẳng (SAC)
A. \(d = \frac{{a\sqrt {39} }}{{13}}.\)
B. \(d=a\)
C. \(d = \frac{{2a\sqrt {39} }}{{13}}.\)
D. \(d = \frac{{a\sqrt {40} }}{{13}}.\)
-
Câu 3:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SBvuông góc với mặt phẳng đáy. Cho biết SB = 3a , AB = 4a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)
A. \( \frac{{12\sqrt {61} a}}{{61}}{\mkern 1mu}\)
B. \( \frac{{2\sqrt {61} a}}{{61}}{\mkern 1mu}\)
C. \( \frac{{12\sqrt {29} a}}{{61}}{\mkern 1mu}\)
D. \( \frac{{12\sqrt {14} a}}{{61}}{\mkern 1mu}\)
-
Câu 4:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên \(SA = a\sqrt 3\) và vuông góc với mặt đáy (ABC). Tính khoảng cách d từ A đến mặt phẳng (SBC)
A. \(d = \frac{{a\sqrt {15} }}{5}\)
B. \(d=a\)
C. \(d = \frac{{a\sqrt {5} }}{5}\)
D. \(d =a\sqrt3\)
-
Câu 5:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC); góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 600. Gọi M là trung điểm của cạnh AB. Tính khoảng cách d từ B đến mặt phẳng (SMC)
A. \(d=a\sqrt3\)
B. \(d = \frac{{a\sqrt {39} }}{{13}}\)
C. \(d=a\)
D. \(d = \frac{{a }}{{2}}\)
-
Câu 6:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính theo a khoảng cách từ điểm A đến mặt phẳng (A'BC)
A. \( \frac{{a\sqrt 2 }}{2}\)
B. \( \frac{{a\sqrt 3 }}{3}\)
C. \( \frac{{a\sqrt 2 }}{3}\)
D. \( \frac{{a\sqrt 2 }}{5}\)
-
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên \( SA = \frac{{a\sqrt {15} }}{2}\) và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ O đến mặt phẳng (SBC).
A. \( d = \frac{{a\sqrt {285} }}{{19}}\)
B. \( d = \frac{{\sqrt {285} }}{{19}}\)
C. \( d = \frac{{a\sqrt {285} }}{{38}}.\)
D. \( d = \frac{{a\sqrt {28} }}{{19}}.\)
-
Câu 8:
Cho hình chóp S.ABCD có đáy (ABCD ) là hình chữ nhật. Tam giác (SAB ) đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD) . Biết \(SD = 2a\sqrt3\) và góc tạo bởi đường thẳng (SC ) và mặt phẳng (ABCD) bằng 300. Tính khoảng cách từ điểm B đến mặt phẳng (SAC)
A. \( \frac{{2a}}{{\sqrt {11} }}\)
B. \( \frac{{2a\sqrt {66} }}{{11}}\)
C. \( \frac{{a\sqrt {15} }}{{5}}\)
D. \({{4\sqrt {15} }}a\)
-
Câu 9:
Cho hình chóp S.ABCD có đáy (ABCD ) là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với đáy, SB hợp với mặt đáy một góc 600 . Tính khoảng cách d từ điểm D đến mặt phẳng (SBC)
A. \(d = \frac{{a\sqrt 3 }}{2}\)
B. \(d = \frac{{\sqrt 3 }}{2}\)
C. \(d =a\)
D. \(d =a\sqrt3\)
-
Câu 10:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a. Biết \(SA = \sqrt3 a \) và SA vuông góc (ABCD). Gọi H là hình chiếu vuông góc của A trên (SBC) Tính khoảng cách d từ H đến mặt phẳng SCD
A. \( d = \frac{{3\sqrt {15} a}}{{60}}\)
B. \( d = \frac{{3\sqrt {30} a}}{{40}}\)
C. \( d = \frac{{3\sqrt {10} a}}{{20}}\)
D. \( d = \frac{{3\sqrt {50} a}}{{80}}\)
-
Câu 11:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AD = a, AB = 2a, BC = 3a, SA = 2a, H là trung điểm cạnh AB, SH là đường cao của hình chóp S.ABCD Tính khoảng cách từ điểm A đến mặt phẳng (SCD).
A. \(\frac{{a\sqrt {30} }}{7}\)
B. \(\frac{{a\sqrt {30} }}{10}\)
C. \(\frac{{a\sqrt {13} }}{7}\)
D. \(\frac{{a\sqrt {17} }}{7}\)
-
Câu 12:
Cho hình chóp (S.ABCD ) có đáy ABCD là hình vuông, \(\frac{{SB}}{{\sqrt 2 }} = \frac{{SC}}{{\sqrt 3 }} = a\). Cạnh SA vuông góc (ABCD), khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
A. \( \frac{a}{{\sqrt 6 }}\)
B. \( \frac{a}{{3}}\)
C. \( \frac{a}{{\sqrt 3 }}\)
D. \( \frac{a}{{\sqrt 2 }}\)
-
Câu 13:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có \( AB = a\sqrt 2 \). Cạnh bên SA = 2a và vuông góc với mặt đáy (ABCD). Tính khoảng cách d từ D đến mặt phẳng (SBC)
A. \(d = \frac{{a\sqrt {10} }}{2}\)
B. \(d=a\sqrt2\)
C. \(d = \frac{{2a\sqrt {3} }}{3}\)
D. \(d = \frac{{a\sqrt {3} }}{3}\)
-
Câu 14:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a. Cạnh bên \( SA = a\sqrt 2 \) và vuông góc với đáy (ABCD). Tính khoảng cách d từ điểm B đến mặt phẳng (SCD)
A. \(d=a\)
B. \( d = \frac{{a\sqrt 6 }}{3}.\)
C. \(d=a\sqrt3\)
D. \( d = \frac{{a\sqrt 6 }}{2}.\)
-
Câu 15:
Cho hình chóp S.ABC có đáy ABC là tam giác cạnh \(BC = a, AC = 2a\sqrt2 , \widehat{ACB} = 45^0\). Cạnh bên SB vuông góc với mặt phẳng (ABC). Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
A. \( \frac{{2a}}{3}.\)
B. \(2a\)
C. \( \frac{{8a}}{3}.\)
D. \( \frac{{3a}}{4}.\)
-
Câu 16:
Cho hình lập phương (ABCD.A'B'C'D' ) có cạnh bằng a. Khoảng cách từ ba điểm nào sau đây đến đường chéo AC' bằng nhau ?
A. A′,B,C′.
B. B′,C′,D′.
C. B,C,D
D. A,A′,D′.
-
Câu 17:
Cho hình lập phương (ABCD.A'B'C'D' ) có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng DB' bằng
A. \(a\sqrt6\)
B. \( \frac{{a\sqrt 6 }}{2}\)
C. \(a\sqrt3\)
D. \( \frac{{a\sqrt 6 }}{3}\)
-
Câu 18:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD' bằng
A. \( \frac{{a\sqrt 6 }}{3}\)
B. \( \frac{{a\sqrt 6 }}{2}\)
C. \( \frac{{a\sqrt 6 }}{5}\)
D. \(a\)
-
Câu 19:
Cho hình lập phương (ABCD.A'B'C'D' ) có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD' bằng
A. \(a\sqrt2\)
B. \( \frac{{a\sqrt 6 }}{2}\)
C. \( \frac{{a\sqrt 3 }}{2}\)
D. \(a\sqrt3\)
-
Câu 20:
Cho hình chóp S.ABC trong đó SA, AB, BC vuông góc với nhau từng đôi một. Biết \( SA = 3a, AB = a\sqrt 3 , BC = a\sqrt 6\) . Khoảng cách từ B đến SC bằng
A. \(a\sqrt2\)
B. \(2a\)
C. \(2a\sqrt3\)
D. \(a\sqrt3\)
-
Câu 21:
Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng alpha . Khoảng cách từ tâm của đáy đến một cạnh bên bằng
A. \( a\sqrt 2 \cot \alpha \)
B. \({{a\sqrt 2 }}{}{\rm{tan}}\alpha \)
C. \(\frac{{a\sqrt 2 }}{2}{\rm{cos}}\alpha \)
D. \(\frac{{a\sqrt 2 }}{2}{\rm{sin}}\alpha \)
-
Câu 22:
Cho hình chóp S.ABCD có SA vuông góc (ABCD), SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
A. \( \frac{{a\sqrt 3 }}{3}\)
B. \( \frac{{a\sqrt 3 }}{4}\)
C. \( \frac{{a\sqrt 2 }}{4}\)
D. \( \frac{{a\sqrt 2 }}{4}\)
-
Câu 23:
Cho hình chóp S.ABCDcó SA vuông góc (ABCD), đáy ABCD là hình thoi cạnh bằng a và \(\hat B = 60^0\) . Biết SA = 2a. Tính khoảng cách từ A đến SC.
A. \(\frac{{3a\sqrt 2 }}{2}\)
B. \(\frac{{4a\sqrt 3 }}{3}\)
C. \(\frac{{2a\sqrt 5 }}{5}\)
D. \(\frac{{5a\sqrt 6 }}{2}\)
-
Câu 24:
Cho hình chóp A.BCDcó cạnh AC vuông góc BCD và BCD là tam giác đều cạnh bằng a. Biết \(AC = a\sqrt 2\) , khoảng cách từ A đến đường thẳng BD bằng:
A. \( \frac{{3a\sqrt 2 }}{2}\)
B. \( \frac{{2a\sqrt3 }}{3}\)
C. \( \frac{{4a\sqrt5 }}{3}\)
D. \( \frac{{a\sqrt{11} }}{2}\)
-
Câu 25:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Khoảng cách từ M đến SA nhận giá trị nào trong các giá trị sau?
A. \( \frac{{a\sqrt 5 }}{2}\)
B. \(2a\sqrt5\)
C. \(a\sqrt2\)
D. \( \frac{{a\sqrt 3 }}{2}\)
-
Câu 26:
Hình chóp đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi H là trung điểm của BC, khoảng cách từ S đến AH bằng:
A. 2a
B. a√3
C. a
D. a√5
-
Câu 27:
Cho hình chóp A.BCD có cạnh AC vuông góc (BCD) và BCD là tam giác đều cạnh bằng a. Biết \(AC = a\sqrt 2\) và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
A. \(a\sqrt {\frac{2}{3}} \)
B. \(a\sqrt {\frac{6}{11}} \)
C. \(a\sqrt {\frac{7}{5}} \)
D. \(a\sqrt {\frac{4}{7}} \)
-
Câu 28:
Cho tứ diện SABC trong đóSA, SB, SC vuông góc với nhau từng đôi một vàSA = 3a, SB = a,SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:
A. \( \frac{{3a\sqrt 2 }}{2}\)
B. \( \frac{{7a\sqrt 5 }}{5}\)
C. \( \frac{{8a\sqrt3 }}{3}\)
D. \( \frac{{7a\sqrt 6 }}{5}\)
-
Câu 29:
Cho hình chóp A.BCD có cạnh AC vuông góc (BCD) và BCD là tam giác đều cạnh bằng a. Biết \( AC = a\sqrt 2\) và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
A. \( a\sqrt {\frac{7}{5}}\)
B. \( a\sqrt {\frac{4}{7}}\)
C. \( a\sqrt {\frac{6}{11}}\)
D. \( a\sqrt {\frac{2}{3}}\)
-
Câu 30:
Cho hình chóp S.ABCD trong đó SA, AB, BC đôi một vuông góc và SA = AB = BC = 1. Khoảng cách giữa hai điểm S và C nhận giá trị nào trong các giá trị sau ?
A. \(\sqrt 2 \)
B. \(\sqrt 3\)
C. \(2\)
D. \( \frac{{\sqrt 3 }}{2}\)
-
Câu 31:
Cho hình chóp O.ABC có đường cao \(OH = \frac{{2a}}{{\sqrt 3 }}\). Gọi M và N lần lượt là trung điểm của OA và OB. Tính khoảng cách giữa đường thẳng MN và (ABC).
A. \(\frac{{a\sqrt 3 }}{3}\)
B. \(\frac{{a\sqrt 2 }}{2}\)
C. \(\frac a2\)
D. \(\frac a 3\)
-
Câu 32:
Cho hai tam giác ABC và ABD nằm trong hai mặt phẳng hợp với nhau một góc 60o. Tam giác ABC cân ở C, tam giác ABD cân ở D. Đường cao DK của tam giác ABD bằng 12cm. Khoảng cách từ D đến (ABC) bằng giá trị nào dưới đây?
A. \(3\sqrt3\) cm
B. \(6\sqrt3\) cm
C. 6 cm
D. \(6\sqrt2\) cm
-
Câu 33:
Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách từ A đến (BCD) bằng bao nhiêu?
A. \(\frac{{a\sqrt 6 }}{2}\)
B. \(\frac{{a\sqrt 6 }}{3}\)
C. \(\frac{{a\sqrt 3 }}{6}\)
D. \(\frac{{a\sqrt 3 }}{3}\)
-
Câu 34:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng A. Khoảng cách từ ba điểm nào sau đây đến đường chéo AC' bằng nhau?
A. A', B, C'
B. B, C, D
C. B', C', D'
D. A, A', D'
-
Câu 35:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Gọi M là trung điểm của CD. Khoảng cách từ M đến (SAB) nhận giá trị nào trong các giá trị sau?
A. \(\frac{{a\sqrt 2 }}{2}\)
B. 2a
C. \(a\sqrt2\)
D. a
-
Câu 36:
Trong mặt phẳng (P) cho tam giác đều ABC cạnh a. Trên tia Ax vuông góc với mặt phẳng (P) lấy điểm S sao cho SA = a. Khoảng cách từ A đến (SBC) bằng bao nhiêu?
A. \(a\sqrt5\)
B. 2a
C. \(\frac{{a\sqrt {21} }}{7}\)
D. \(a\sqrt3\)
-
Câu 37:
Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a2. Khoảng cách từ S đến BC bằng bao nhiêu?
A. 2a
B. 4a
C. 3a
D. 5a
-
Câu 38:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
B. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc với cả hai đường thẳng đó.
C. Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng kia.
D. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó cắt cả hai đường thẳng đó.
-
Câu 39:
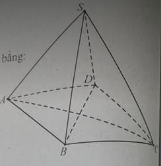
Cho chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a.
Khoảng cách từ D đến mặt phẳng (SAC) bằng:
A. a
B. \(\frac{a}{2}\)
C. \(\frac{{a\sqrt 2 }}{3}\)
D. \(\frac{{a\sqrt 2 }}{2}\)
-
Câu 40:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Giả sử góc BAD bằng 60o. Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng:
A. \(\frac{{2a\sqrt 2 }}{3}\)
B. \(\frac{{a\sqrt 3 }}{2}\)
C. a
D. \(a\sqrt 3\)
