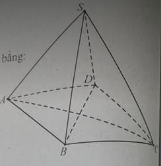
Cho hình chóp S.ABCD có đáy (ABCD ) là hình vuông cạnh bằng a. Cạnh bên SA vuông góc với đáy, SB hợp với mặt đáy một góc 600 . Tính khoảng cách d từ điểm D đến mặt phẳng (SBC)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXác định
\( {60^0} = \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} \Rightarrow SA = AB.\tan \widehat {SBA} = a\sqrt 3 \)
Ta có
\( AD\parallel BC \Rightarrow AD\parallel \left( {SBC} \right) \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right)\)
Kẻ AK⊥SB(1)
Ta có:
\(\left\{ \begin{array}{l} BC \bot SA\\ BC \bot AB \end{array} \right. \to BC \bot (SAB) \to BC \bot AK(2)\)
Từ (1) và (2) ⇒ AK⊥(SBC)
Khi đó:
\( d\left( {A;\left( {SBC} \right)} \right) = AK = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{a\sqrt 3 }}{2}.\)



.PNG)
.png)