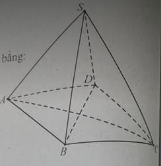
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với AB = 2a. Tam giác SAB vuông tại S, mặt phẳng \(\left( {SAB} \right)\) vuông góc với \(\left( {ABCD} \right)\). Biết góc tạo bởi đường thẳng SD và mặt phẳng \(\left( {SBC} \right)\) bằng \(\varphi \), với \(\sin \varphi = \frac{1}{3}\). Tính khoảng cách từ C đến \(\left( {SBD} \right)\) theo a.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi d là giao tuyến của \(\left( {SBC} \right)\) và \(\left( {SAD} \right)\) thì d qua S và song song với AD.
Kẻ qua D đường thẳng song song với SA, cắt d tại K, ta có:
\(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\AD \bot AB\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right) \Rightarrow AD \bot SA \Rightarrow d \bot SA \Rightarrow d \bot KD\,\,\left( 1 \right)\).
\(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {SAD} \right)\\SB \bot SA\end{array} \right. \Rightarrow SB \bot \left( {SAD} \right) \Rightarrow SB \bot KD\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(KD \bot \left( {SBC} \right)\), hay góc giữa SD với \(\left( {SBC} \right)\) bằng góc giữa SD với SK và bằng góc \(\widehat {KSD}\) (do tam giác KSD vuông tại K). Suy ra \(\widehat {KSD} = \varphi \).
Có \(\sin \varphi = \frac{1}{3} \Leftrightarrow \frac{{SA}}{{SD}} = \frac{1}{3} \Leftrightarrow \frac{{SA}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{1}{3} \Leftrightarrow 9S{A^2} = S{A^2} + 4{a^2} \Leftrightarrow SA = \frac{a}{{\sqrt 2 }}\).
Ta có \(S{B^2} = A{B^2} – S{A^2} = 4{a^2} – \frac{{{a^2}}}{2} = \frac{{7{a^2}}}{2} \Rightarrow SB = \frac{{a\sqrt {14} }}{2}\).
Gọi H là chân đường vuông góc hạ từ S của tam giác SAB, do \(\left( {SAB} \right) \bot \left( {ABCD} \right)\) nên \(SH \bot \left( {ABCD} \right)\).
Ta có
\(\begin{array}{l}d\left( {C,\left( {SBD} \right)} \right) = d\left( {A,\left( {SBD} \right)} \right) = \frac{{AB}}{{HB}}d\left( {H,\left( {SBD} \right)} \right)\\ = \frac{{A{B^2}}}{{HB.AB}}d\left( {H,\left( {SBD} \right)} \right) = \frac{{A{B^2}}}{{S{B^2}}}d\left( {H,\left( {SBD} \right)} \right)\\ = \frac{{4{a^2}}}{{\frac{{7{a^2}}}{2}}}.d\left( {H,\left( {SBD} \right)} \right) = \frac{8}{7}.d\left( {H,\left( {SBD} \right)} \right)\end{array}\)
Tam giác SAB vuông tại S nên:
\(\frac{1}{{S{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}} = \frac{2}{{{a^2}}} + \frac{2}{{7{a^2}}} = \frac{{16}}{{7{a^2}}} \Rightarrow SH = \frac{{a\sqrt 7 }}{4}\).
Gọi O là tâm của hình vuông thì \(OA = \frac{{AC}}{2} = \frac{{2a\sqrt 2 }}{2} = a\sqrt 2 \).
Gọi E là hình chiếu vuông góc của H lên OB ta có
\(\frac{{HE}}{{AO}} = \frac{{BH}}{{BA}} = \frac{{BH.BA}}{{B{A^2}}} = \frac{{S{B^2}}}{{B{A^2}}} = \frac{{\frac{{7{a^2}}}{2}}}{{4{a^2}}} = \frac{7}{8} \Rightarrow HE = \frac{7}{8}.a\sqrt 2 = \frac{{7\sqrt 2 a}}{8}\).
Gọi F là hình chiếu vuông góc của H lên SE, dễ thấy \(d\left( {H,\left( {SBD} \right)} \right) = HF\).
Có \(\frac{1}{{H{F^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{E^2}}} = \frac{{16}}{{7{a^2}}} + \frac{{32}}{{49{a^2}}} = \frac{{144}}{{49{a^2}}} \Rightarrow HF = \frac{{7a}}{{12}}\), suy ra \(d\left( {H,\left( {SBD} \right)} \right) = \frac{{7a}}{{12}}\)
Vậy \(d\left( {C,\left( {SBD} \right)} \right) = \frac{8}{7}d\left( {H,\left( {SBD} \right)} \right) = \frac{8}{7}.\frac{{7a}}{{12}} = \frac{{2a}}{3}\)
