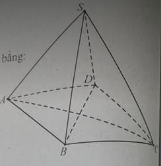
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D, \(SA \bot \left( {ABCD} \right)\); AB = 2a, AD = CD = a. Gọi N là trung điểm SA. Tính khoảng cách giữa 2 đường thẳng SC và DN, biết rằng thể tích khối chóp S.ABCD bằng \(\frac{{{a^3}\sqrt 6 }}{2}\).
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Ta có \({V_{S.ABCD}} = \frac{1}{3}SA.{S_{ABCD}}; {S_{ABCD}} = \frac{1}{2}\left( {a + 2a} \right).a = \frac{{3{a^2}}}{2}\)
Suy ra \(SA = \frac{{3{V_{S.ABCD}}}}{{{S_{ABCD}}}} = \frac{{3{a^3}\sqrt 6 }}{2}.\frac{2}{{3{a^2}}} = a\sqrt 6 \).
Gọi M là trung điểm của AB, O là giao điểm của AC và DM.
Ta có tứ giác ADCM là hình vuông cạnh a.
Ta có \(\left( {DNM} \right)\) chứa ON và \(ON{\rm{//}}SC\) nên \(SC{\rm{//}}\left( {DNM} \right)\).
Suy ra nên \(d\left( {SC,DN} \right) = d\left( {SC,\left( {DMN} \right)} \right) = d\left( {C,\left( {DMN} \right)} \right) = d\left( {A,\left( {DMN} \right)} \right)\).
Trong \(\left( {SAC} \right)\) kẻ \(AH \bot NO\). Ta có \(DM \bot AC\) và \(DM \bot SA\) nên \(DM \bot \left( {SAC} \right)\)
Khi đó ta có
\(\left. \begin{array}{l}AH \bot NO\\AH \bot DM\left( {DM \bot \left( {SAC} \right)} \right)\end{array} \right\} \Rightarrow AH \bot \left( {DMN} \right)\)
\( \Rightarrow d\left( {A,\left( {DMN} \right)} \right) = AH\).
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{N^2}}} + \frac{1}{{A{O^2}}} ; AN = \frac{{a\sqrt 6 }}{2}; AO = \frac{{a\sqrt 2 }}{2} \Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{{{\frac{a}{2}}^2}}} + \frac{1}{{\frac{{3{a^2}}}{2}}} = \frac{8}{{3{a^2}}} \Rightarrow AH = \frac{{a\sqrt 6 }}{4}\).
Vậy \(d\left( {SC,DN} \right) = \frac{{a\sqrt 6 }}{4}\)
