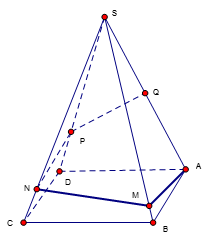
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a và cạnh bên bằng \(\frac{{a\sqrt {37} }}{3}\). Gọi M là trung điểm cạnh SA. Tính khoảng cách giữa hai đường thẳng AC và BM.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi D là đỉnh thứ tư của hình bình hành ABDC.
Khi đó, \(AC\,{\rm{//}}\,BD \Rightarrow AC\,{\rm{//}}\,\left( {MBD} \right) \Rightarrow {\rm{d}}\left( {AC\,,\,BM} \right) = {\rm{d}}\left( {AC\,,\,\left( {MBD} \right)} \right) = {\rm{d}}\left( {A\,,\,\left( {MBD} \right)} \right)\).
Gọi O là trọng tâm tam giác ABC. Suy ra \(SO \bot \left( {ABC} \right)\).
Gọi H là trung điểm AO. Suy ra \(MH\,{\rm{//}}\,SO \Rightarrow MH \bot \left( {ABC} \right)\).
Vẽ \(HK \bot BD\) tại K. Suy ra \(HK\,{\rm{//}}\,BO\). Suy ra \(\frac{{BO}}{{HK}} = \frac{{OD}}{{HD}} = \frac{4}{5} \Rightarrow HK = \frac{5}{4}BO\).
Mà \(BO = \frac{2}{3}\,.\,2a\,.\,\frac{{\sqrt 3 }}{2} = \frac{{2a\sqrt 3 }}{3}\) suy ra \(HK = \frac{5}{4}.\frac{{2a\sqrt 3 }}{3} = \frac{{5a\sqrt 3 }}{6}\).
Vẽ \(HI \bot MK\) tại I. Suy ra \({\rm{d}}\left( {H\,,\,\left( {MBD} \right)} \right) = HI\).
Ta có, \(S{O^2} = S{A^2} – A{O^2} = {\left( {\frac{{a\sqrt {37} }}{3}} \right)^2} – {\left( {\frac{{2a\sqrt 3 }}{3}} \right)^2} = \frac{{25a}}{9} \Rightarrow SO = \frac{{5a}}{3} \Rightarrow MH = \frac{{5a}}{6}\)
Mà \(\frac{1}{{H{I^2}}} = \frac{1}{{M{H^2}}} + \frac{1}{{H{K^2}}}\) suy ra \(HI = \frac{{5a\sqrt 3 }}{{12}} \Rightarrow {\rm{d}}\left( {H\,,\,\left( {MBD} \right)} \right) = HI = \frac{{5a\sqrt 3 }}{{12}}\).
Mà \(\frac{{{\rm{d}}\left( {H\,,\,\left( {MBD} \right)} \right)}}{{{\rm{d}}\left( {A\,,\,\left( {MBD} \right)} \right)}} = \frac{{HD}}{{AD}} = \frac{5}{6} \Rightarrow {\rm{d}}\left( {A\,,\,\left( {MBD} \right)} \right) = \frac{{a\sqrt 3 }}{2}\)
Vậy \({\rm{d}}\left( {AC\,,\,BM} \right) = \frac{{a\sqrt 3 }}{2}\)



.png)